统计学中有时会用到 PP 图 或 QQ 图,用来看样本数据是否服从某一特定分布。
若 PP 或 QQ 图中的点基本落在一条 45度 的线上,则说明服从特定分布。
一般的步骤为:
- 将样本数据从小到大排序,假设排序后的样本数据为 x 1 x_1 x1, x 2 x_2 x2, … dots …, x n x_n xn。
- 对于 n n n 个样本数据,对应 n n n 个分位数。分位数的取值规则不一样,一个比较简答的规则是:第 k k k 个分位数的取值为 Q k = ( k − 0.5 ) / n Q_k=(k-0.5)/n Qk=(k−0.5)/n
- 横坐标为: x 1 x_1 x1, x 2 x_2 x2, … dots …, x n x_n xn,纵坐标为:所判断分布的累计分布函数在分位数的逆函数值 F − ( Q k ) F^-(Q_k) F−(Qk),则为 QQ 图;若横坐标为: F ( x 1 ) F(x_1) F(x1), F ( x 2 ) F(x_2) F(x2), … dots …, F ( x n ) F(x_n) F(xn),纵坐标为: Q k Q_k Qk,则为 PP 图。
PP 图与 QQ 图的功能基本一样,我见用 QQ 图的比较多。因为分位数的取值规则不一样,因此 QQ 图可能画的不太一样。
下面以正态分布的随机样本为例,用 python 画一下图形,专门的 QQ 图也可以调用 statsmodels 中的 ProbPlot 函数 (不是 scipy 中的 probplot,因为 scipy 中的 probplot 画的直线是拟合直线,并不是45度斜线)。
import scipy.stats as st
import matplotlib.pyplot as plt
import numpy as np
import statsmodels.api as sm
probplot = sm.ProbPlot(samples, dist = st.norm, loc = 5, scale = 2)
probplot.qqplot(line='45')
n = 100
samples = st.norm.rvs(loc = 5, scale = 2, size = n)
samples_sort = sorted(samples)
x_labels_q = samples_sort
y_labels_q = st.norm.ppf(x_labels_p, loc = 5, scale = 2)
plt.scatter(x_labels_q, y_labels_q)
plt.title('QQ plot for normal distribution samle')
plt.show()
x_labels_p = np.arange(1/(2*n), 1, 1/n)
y_labels_p = st.norm.cdf(samples_sort, loc = 5, scale = 2)
plt.scatter(x_labels_p, y_labels_p)
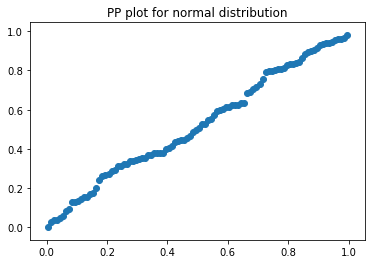
plt.title('PP plot for normal distribution samle')
plt.show()
显示图形:
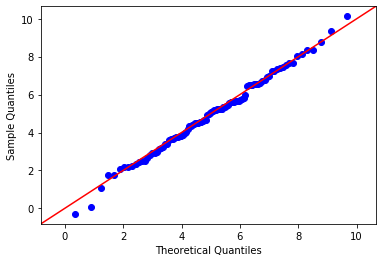
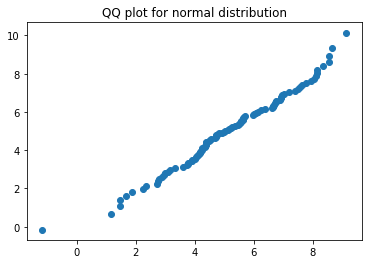
由于 ProbPlot 的分位数取值规则不同,从图形上看,ProbPlot 的 QQ 图与自己画的 QQ 图略微不一样。
转载于个人公众号:Python 统计分析与数据科学

最后
以上就是深情蓝天最近收集整理的关于PP图,QQ 图,及 python 画图的全部内容,更多相关PP图,QQ内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复