Python求解拉普拉斯矩阵及其特征值

学习心得

（1）laplacian matrix就是无向图中定义 $L=D-A$，其中D为邻接矩阵，A为度矩阵（是一个对角矩阵）。本文用的python计算拉普拉斯矩阵及其特征值、特征向量。
（2）numpy中文文档：https://www.numpy.org.cn/user/，可以配spyder看对应变量的矩阵元素。
（3）求图拉普拉斯矩阵的特征值：时间复杂度是$O(n^3)$（n为节点数），所以当图很大时用该方法效率很低。

一、背景介绍

1.1 图论基础

定义一（图的邻接矩阵）：

• 给定一个图 G = { V , E } mathcal{G}={mathcal{V}, mathcal{E}} G={V,E}，其对应的邻接矩阵被记为 A ∈ { 0 , 1 } N × N mathbf{A} in{0,1}^{N times N} A∈{0,1}N×N。${\mathbf{A}}_{i,j}=1$表示存在从结点$v_i$到$v_j$的边，反之表示不存在从结点$v_i$到$v_j$的边。

• 在无向图中，从结点$v_i$到$v_j$的边存在，意味着从结点$v_j$到$v_i$的边也存在。因而无向图的邻接矩阵是对称的。

• 在无权图中，各条边的权重被认为是等价的，即认为各条边的权重为$1$。

• 对于有权图，其对应的邻接矩阵通常被记为 W ∈ { 0 , 1 } N × N mathbf{W} in{0,1}^{N times N} W∈{0,1}N×N，其中${\mathbf{W}}_{i,j}=w_{ij}$表示从结点$v_i$到$v_j$的边的权重。若边不存在时，边的权重为$0$。

  一个无向无权图的例子：
  
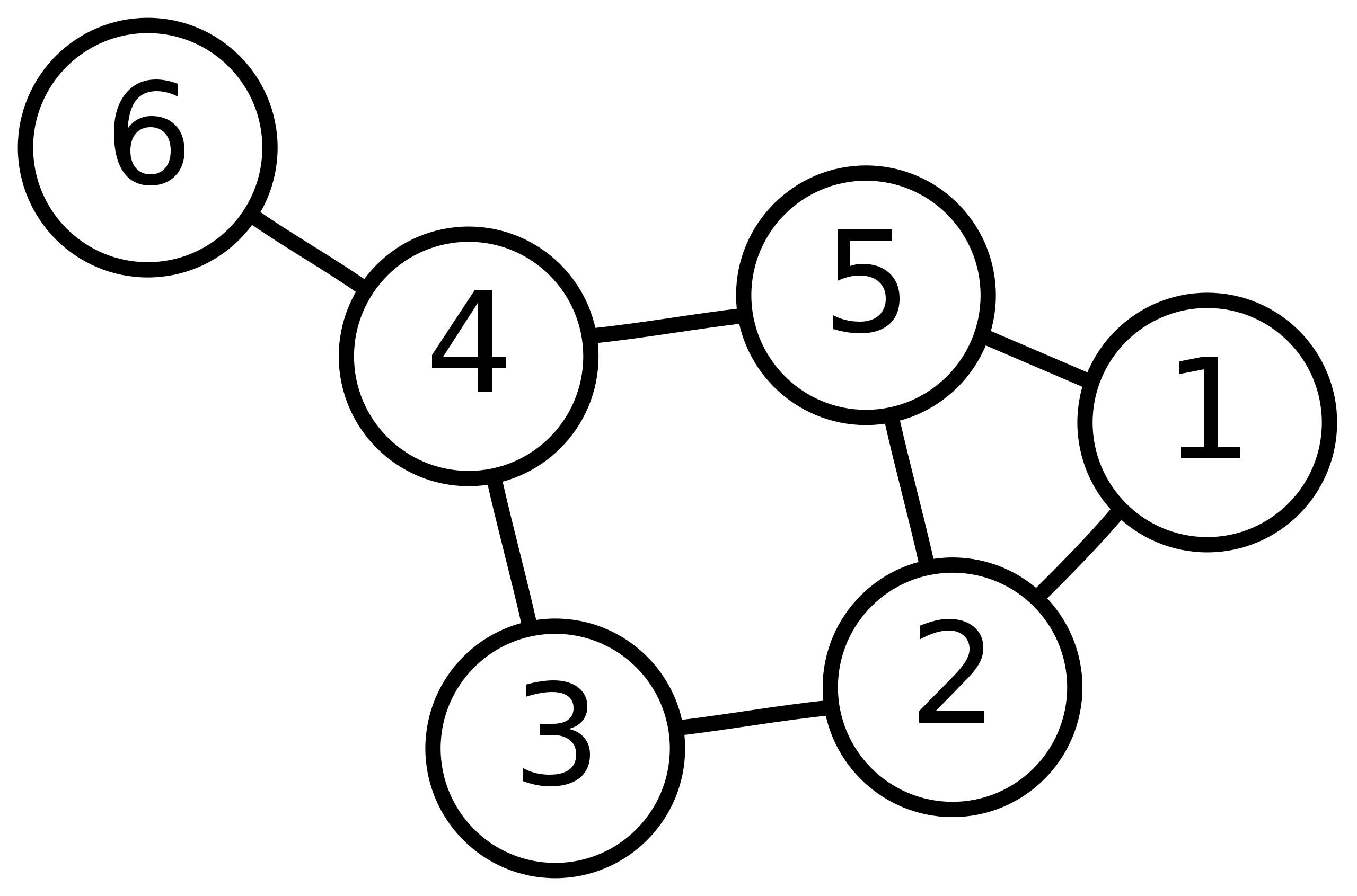
  其邻接矩阵为：
  $$\mathbf{A}=\left(\begin{array}{lllll}0& 1& 0& 1& 1\\ 1& 0& 1& 0& 0\\ 0& 1& 0& 0& 1\\ 1& 0& 0& 0& 1\\ 1& 0& 1& 1& 0\end{array}\right)$$

定义二（拉普拉斯矩阵，Laplacian Matrix）：

• 给定一个图 G = { V , E } mathcal{G}={mathcal{V}, mathcal{E}} G={V,E}，其邻接矩阵为$A$，其拉普拉斯矩阵定义为$\mathbf{L}=\mathbf{D}-\mathbf{A}$，其中度矩阵 $\mathbf{D}=\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{g}(\mathbf{d}({\mathbf{v}}_1),\cdots ,\mathbf{d}({\mathbf{v}}_{\mathbf{N}}))$。

定义三（对称归一化的拉普拉斯矩阵，Symmetric normalized Laplacian）：

• 给定一个图 G = { V , E } mathcal{G}={mathcal{V}, mathcal{E}} G={V,E}，其邻接矩阵为$A$，其规范化的拉普拉斯矩阵定义为

$$\mathbf{L}={\mathbf{D}}^{-\frac{1}{2}}(\mathbf{D}-\mathbf{A}){\mathbf{D}}^{-\frac{1}{2}}=\mathbf{I}-{\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}$$

1.2 拉普拉斯矩阵的变体

节点数为$n$的简单图$G$，$A$是$G$的邻接矩阵，则如上面介绍的那样，$G$的拉普拉斯矩阵即$L=D-A$。
（1）对称归一化后的拉普拉斯矩阵：$$L^{sys}=D^{-1/2}L{D}^{-1/2}=I-D^{-1/2}A{D}^{-1/2}$$
（2）随机游走归一化的拉普拉斯矩阵：$$\begin{array}{rl}& L^{rw}=D^{-1}L=I-D^{-1}A\\ & L_{i,j}^{rw}:=\{\begin{array}{ll}1& \mathrm{i}=\mathrm{j}\\ \frac{-1}{\sqrt{\mathrm{diag}\left(v_i\right)}}& \text{ if }i\ne j\text{ and }{v}_i\text{ adjacent to }{v}_j\\ 0& \text{ othewise }\end{array}\end{array}$$

1.3 拉普拉斯矩阵的优良性质：

• 拉普拉斯矩阵是半正定对称矩阵
• 对称矩阵有n个线性无关的特征向量，n是Graph中节点的个数 $\Rightarrow$ 拉普拉斯矩阵可以特征分解
• 半正定矩阵的特征值非负
• 对称矩阵的特征向量构成的矩阵为正交阵 $\Rightarrow U^{T}U=E$

1.4 GCN为啥要用拉普拉斯矩阵

• 拉普拉斯矩阵可以谱分解（特征分解）GCN是从谱域的角度提取拓扑图的空间特征的。
• 拉普拉斯矩阵只在中心元素和一阶相邻元素处有非零元素，其他位置皆为0.
• 传统傅里叶变换公式中的基函数是拉普拉斯算子，借助拉普拉斯矩阵，通过类比可以推导出Graph上的傅里叶变换公式。

二、Python代码实现

这是networkX库对稀疏矩阵A的处理方式，有少量改进（将所有内容保持稀疏）：

n,m = A.shape
diags = A.sum(axis=1)
D = sps.spdiags(diags.flatten(), [0], m, n, format='csr')
D - A

numpy和scipy两个库中模块中都提供了线性代数的库linalg，但scipy的linalg的更全面一些。

# laplacian矩阵
import numpy as np
def unnormalized_laplacian(adj_matrix):
    # 先求度矩阵
    R = np.sum(adj_matrix, axis=1)
    degreeMatrix = np.diag(R)
    return degreeMatrix - adj_matrix
    
# 对称归一化的laplacian矩阵
def normalized_laplacian(adj_matrix):
    R = np.sum(adj_matrix, axis=1)
    R_sqrt = 1/np.sqrt(R)
    D_sqrt = np.diag(R_sqrt)
    I = np.eye(adj_matrix.shape[0])
    return I - np.matmul(np.matmul(D_sqrt, adj_matrix), D_sqrt)

matlab的代码实现为：

L = diag(sum(A,2)) - A   % or L=diag(sum(A))-A because A is symmetric

那么如何求矩阵的特征值呢——利用numpy的linalg.eig：

# !/usr/bin/python
## -*-coding:utf-8 -*-

import numpy as np
A = np.array([[3,-1],[-1,3]])
print('打印A：n{}'.format(A))
a, b = np.linalg.eig(A)
print('打印特征值a：n{}'.format(a))
print('打印特征向量b：n{}'.format(b))

得到特征值和特征向量：

打印A：  
[[ 3 -1] 
 [-1  3]]
打印特征值a：
[4. 2.]
打印特征向量b：
[[ 0.70710678  0.70710678] 
 [-0.70710678  0.70710678]]

三阶矩阵试试，回归考研线代的题目：

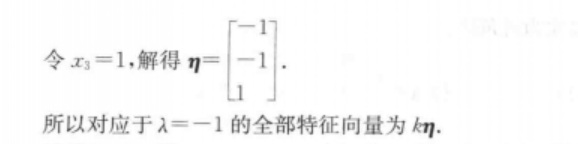
import numpy as np
A = np.array([[2,-3,1],[1,-2,1],[1,-3,2]])
print('打印A：n{}'.format(A))
a, b = np.linalg.eig(A)
print('打印特征值a：n{}'.format(a))
print('打印特征向量b：n{}'.format(b))

结果如下，看结果的特征向量矩阵，每一列代表一个一个特征向量，都是

打印A：
[[ 2 -3  1]
 [ 1 -2  1]
 [ 1 -3  2]]
打印特征值a：
[2.09037533e-15+0.00000000e+00j 1.00000000e+00+5.87474805e-16j
 1.00000000e+00-5.87474805e-16j]
打印特征向量b：
[[0.57735027+0.j         0.84946664+0.j         0.84946664-0.j        ]
 [0.57735027+0.j         0.34188085-0.11423045j 0.34188085+0.11423045j]
 [0.57735027+0.j         0.17617591-0.34269135j 0.17617591+0.34269135j]]

三、关于图Fourier变换

根据卷积原理，卷积公式可以写成
f ∗ g = F − 1 { F { f } ⋅ F { g } } f * g=mathcal{F}^{-1}{mathcal{F}{f} cdot mathcal{F}{g}} f∗g=F−1{F{f}⋅F{g}}
正、逆Fourier变换
$$\mathcal{F}(v)={\int }_{\mathrm{R}}f(x)e^{-2\pi ix\cdot v}dx$$

$$f(x)={\int }_{\mathbb{R}}\mathcal{F}(v)e^{2\pi ix\cdot v}dv$$

一阶导数定义
$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$
拉普拉斯相当于二阶导数
$$\Delta f(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-2f(x)+f(x-h)}{h^2}$$
在graph上，定义一阶导数为
$$f_{\ast g}^{\prime }(x)=f(x)-f(y)$$
对应的拉普拉斯算子定义为
$${\Delta }_{\ast g}{f}^{\prime }(x)={\Sigma }_{y\sim x}(f(x)-f(y))$$
假设$D$为$N\times N$的度矩阵(degree matrix)
$$D(i,j)=\{\begin{array}{ll}{d}_i& \text{ if }i=j\\ 0& \text{ otherwise }\end{array}$$
$A$为$N\times N$的邻接矩阵(adjacency matrix)
$$A(i,j)=\{\begin{array}{ll}1& \text{ if }{x}_i\sim x_j\\ 0& \text{ otherwise }\end{array}$$
那么图上的Laplacian算子可以写成
$$L=D-A$$
标准化后得到
$$L=I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$$
定义Laplacian算子的目的是为了找到Fourier变换的基。

传统Fourier变换的基就是Laplacian算子的一组特征向量
$$\Delta e^{2\pi ix\cdot v}=\lambda e^{2\pi ix\cdot v}$$
类似的，在graph上，有
$$\Delta f=(D-A)f=Lf$$
图拉普拉斯算子作用在由图节点信息构成的向量$f$上得到的结果等于图拉普拉斯矩阵和向量$f$的点积。

那么graph上的Fourier基就是$L$矩阵的$n$个特征向量$U=\left[u_1\dots u_n\right]$，$L$可以分解成$L=U\Lambda U^T$，其中，$\Lambda$是特征值组成的对角矩阵。

传统的Fourier变换与graph的Fourier变换区别

将$f(i)$看成是第$i$个点上的signal，用向量$x=(f(1)\dots f(n))\in {\mathbb{R}}^n$来表示。矩阵形式的graph的Fourier变换为
G F { x } = U T x mathcal{G F}{x}=U^{T} x GF{x}=UTx
类似的graph上的Fourier逆变换为
I G F { x } = U x mathcal{I} mathcal{G} mathcal{F}{x}=U x IGF{x}=Ux

Reference

（1）Python计算特征值与特征向量案例
（2）numpy的linalg官方文档：https://docs.scipy.org/doc/numpy-1.13.0/reference/routines.linalg.html
（3）用python求解特征向量和拉普拉斯矩阵
（4）图卷积网络(GCN)原理解析

最后

以上就是无心衬衫为你收集整理的Python求解拉普拉斯矩阵及其特征值的全部内容，希望文章能够帮你解决Python求解拉普拉斯矩阵及其特征值所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。