BUAA数据结构第七次编程题——北京地铁乘坐线路查询
- 看前须知
- 第七次上机题汇总
- 题目内容
- 问题描述
- 输入形式
- 输出形式
- 样例
- 样例说明
- 题解
- 思考和详解
- 参考代码
- 补充测试的数据
- 最短路径算法小拓
看前须知
要点介绍和简要声明.
第七次上机题汇总
图遍历(图-基本题)——邻接矩阵远比邻接表简单且好操作.
独立路径数计算——DFS+回溯.
最少布线(图)——Prim(BFS+贪心)+kruskal(并查集)双解法+原理解释.
北京地铁乘坐线路查询——Dijkstra和Floyd双解法.
题目内容
问题描述
编写一个程序实现北京地铁最短乘坐(站)线路查询,输入为起始站名和目的站名,输出为从起始站到目的站的最短乘坐站换乘线路。注:1. 要求采用Dijkstra算法实现;2)如果两站间存在多条最短路径,找出其中的一条就行。
输入形式
文件bgstations.txt为数据文件( 点击此处下载,提取码:1234.),包含北京地铁的线路及车站信息。其格式如下:
<地铁线路总条数>
<线路1> <线路1站数>
<站名1> <换乘状态>
<站名2> <换乘状态>
…
<线路2> <线路2站数>
<站名1> <换乘状态>
<站名2> <换乘状态>
…
说明:文件第一行为地铁总线路数;第二行第一个数为某条地铁线线号(如,1为1号线),第二个数为该条地铁线的总站数(如1号线共有23站),两数之间由一个空格分隔;第三行两个数据分别为地铁站名及换乘状态(0为非换乘站,1为换乘站),两数据间由一个空格分隔;以下同,依次为该线地铁其它站信息。在一条线路信息之后是下条地铁线路信息,格式相同。若某条地铁线为环线,则首站与末站信息相同(如北京地铁2号线,首站信息“西直门 1” ,末站信息为“西直门 1”)。例如本题提供的bgstations.txt文件(可从课程网站中课程信息处下载)内容如下:
13
1 23
苹果园 0
古城 0
八角游乐园 0
八宝山 0
玉泉路 0
五棵松 0
万寿路 0
公主坟 1
军事博物馆 1
木樨地 0
南礼士路 0
复兴门 1
西单 1
…
2 19
西直门 1
积水潭 0
鼓楼大街 1
…
西直门 1
…
该文件表明当前北京地铁共有13条线路(不含郊区线路),接着为每条线路信息。
打开当前目录下文件bgstations.txt,读入地铁线路信息,并从标准输入中读入起始站和目的站名(均为字符串,各占一行)。
输出形式
输出从起始站到目的站的乘坐信息,要求乘坐站数最少。换乘信息格式如下:
SSN-n1(m1)-S1-n2(m2)-…-ESN
其中:SSN和ESN分别为起始站名和目的站名;n为乘坐的地铁线路号,m为乘坐站数。
样例
【样例输入】
西土城
北京西站
【样例输出】
西土城-10(1)-知春路-13(2)-西直门-4(2)-国家图书馆-9(4)-北京西站
(或西土城-10(1)-知春路-13(2)-西直门-2(1)-车公庄-6(2)-白石桥南-9(3)-北京西站)
样例说明
打开文件bgstations.txt,读入地铁线路信息,并从标准输入中读入查询起始站名为“西土城”,目的站名为“北京西站”。程序运行结果两站间最少乘坐站数的乘坐方式为“西土城站乘坐10号线1站至知春路站换乘13号线乘坐2站至西直门站换乘4号线乘坐2站至国家图书馆站换乘9号线乘坐4站至北京西站”。本样例存在两条最少站数的乘坐方式,只要找出一条就可以。
题解
思考和详解
这道题有点挑战性,如果不借助任何外力独自一人写完,我只能说你很厉害!
言归正传,首先,这道题分为几个步骤,第一个步骤为初始化图,第二个步骤为建图,第三个步骤为寻找最短路径,第四个步骤为打印输出。
第一个步骤:初始化图。很简单,只需要两个for即可,但是这道题的初始化稍微有点区别,以往的初始化对角线顶点的权重为0,但是这道题必须全部设置为INF,不然之后的最短路径无法计算。
第二个步骤:交叉建图。这个步骤技巧性要求是在是有点高,毕竟这是一个完全模拟的过程,怎么通过给的信息构建一个数据结构是重中之重。在这道题上,我们必须抛弃以前那种直接给出边的信息然后无脑建图的思想。首先我们必须明确一点的是:相邻两站一定联通。这是我们建图的第一原则,必须牢记。**其次,我们必须给每一个站一个特殊的序号,只有有了特殊的序号,我们才可以构建邻接矩阵和运用最短路径算法。**有了以上两点之后,这道题就可以采用交叉建图了。具体操作是这样的,一开始读取一个站名,看看这个站名有没有出现过,如果没有,则加入站名的数组,同时赋予数组下标为其序号,如果出现过,则不添加,同时把这个站的序号作为边的一个顶点,然后继续读入一个站名,这时,先看看数组里之前有没有,如果有就读出序号,如果没有则赋予序号,作为边的另一个顶点,此时就可以构建一条边了(第一原则),然后终点变成下一个将要读入地铁站的起点。为什么叫交叉建图是因为当有换乘站的时候,我们可以直接读取之前的序号数组完成建图,而不是重新弄个新节点存储信息。
第三个步骤:最短路径。Dijkstra,Floyd和Bellman-Ford三种算法都可以,这里只提供前两种,最后一种解决负权边比较多。
第四个步骤:打印输出。首先要注意的是最短路径算法提供的路径数组是跟踪数组,不是真正的最短路径编号,所以要路径回溯(借用栈),之后打印输出还有一个需要注意的地方是判断换乘的条件其实就是判断路线的编号是否不同。
特别提醒:地铁10号线等线是环路,环路的第一站(比如说:巴沟)不可以算是换乘站(测试点有)换乘条件判断要特别注意
最后告诉你们一个小秘密,测评机里的txt信息与我们手头上的不一样,所以我们自己测试是对的在测评机上不一定正确。
应评论区的需求(博主对于评论区可是有求必应啊),我临时增加了一份只有换乘站个起点终点站构图(即忽略中间站)的题解。本题解由2073 陶索梓(网名,不是真名)大哥提供的,但是没有注释,可以参考。
参考代码
Dijkstra
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define M 618
#define INF 0x3f3f3f3f
struct station{ //地铁站序号结构体
char stationName[30]; //站名
int IsChange; //能否换乘
};
struct vertex{ //地铁图结构体
int weight; //权重
int lineID; //路线序号
};
struct station StationID_list[M]; //地铁站序号数组
struct vertex map[M][M]; //地铁图
int lineID,StationNum,lineNum,IsChange,VerNum; //路线序号,一条路线中地铁站个数,路线个数,是否换乘,总地铁站个数
int prev[M],dist[M],path[M],top,pathID[M][M]; //跟踪数组,最短路径数值数组,dijkstra最短路径编号数组,栈顶,Floyd最短路径编号数组
char StationBegin[30],StationEnd[30]; //起点站,终点站
void DrawSubwayMap(FILE *fp); //建图
int SearchMap(char *s); //找站名是否出现过
void dijkstra(int vs, int ve); //dijkstra算法
void PrintPath(int v1,int v2); //打印路径
int main()
{
int i,j,v1,v2,t;
FILE *fp = fopen("bgstations.txt","r");
scanf("%s %s",StationBegin,StationEnd);
for(i=0;i<M;i++) //初始化图
for(j=0;j<M;j++)
{
map[i][j].weight=map[j][i].weight=INF; //权重无穷大
map[i][j].lineID=map[j][i].lineID=0; //编号为0
}
DrawSubwayMap(fp); //建图
v1=SearchMap(StationBegin); //找到起点站编号
v2=SearchMap(StationEnd); //找到终点站编号
dijkstra(v1,v2); //找最短路
for(t=v2;t!=v1;t=prev[t]) //路径追溯
{
path[top]=t;
top++;
}
PrintPath(v1,v2); //打印编号
return 0;
}
void DrawSubwayMap(FILE *fp)
{
int i,j,ContainID,EdgeLast;//两个变量,存在的地铁站的编号,边的起点
char stationName[30]; //站名
fscanf(fp,"%d",&lineNum);
for(i=0;i<lineNum;i++)
{
fscanf(fp,"%d %d",&lineID,&StationNum);
EdgeLast=-1; //每一条路线一开始都是 -1
for(j=0;j<StationNum;j++)
{
fscanf(fp,"%s %d",stationName,&IsChange);
ContainID=SearchMap(stationName); //看看有没有
if(ContainID == -1) //没有
{
strcpy(StationID_list[VerNum].stationName,stationName); //存储
StationID_list[VerNum].IsChange=IsChange; //存储
if(EdgeLast != -1) //如果有边的起点
{
map[EdgeLast][VerNum].lineID=map[VerNum][EdgeLast].lineID=lineID; //存储
map[EdgeLast][VerNum].weight=map[VerNum][EdgeLast].weight=1; //存储
}
EdgeLast=VerNum; //终点变起点
VerNum++; //总数 +1
}
else
{
if(EdgeLast != -1) //如果有边的起点
{
map[EdgeLast][ContainID].lineID=map[ContainID][EdgeLast].lineID=lineID;//存储
map[EdgeLast][ContainID].weight=map[ContainID][EdgeLast].weight=1; //存储
}
EdgeLast = ContainID; //终点变起点
}
}
}
}
int SearchMap(char *s)
{
int i;
for(i=0;i<VerNum;i++)
if(strcmp(s,StationID_list[i].stationName)==0)
return i; //返回序号
return -1;
}
void dijkstra(int vs, int ve)
{
int i,j,k,min,tmp;
int flag[M]; // flag[i]=1表示"顶点vs"到"顶点i"的最短路径已成功获取。
for (i = 0; i < VerNum; i++) // 初始化
{
flag[i] = 0; // 顶点i的最短路径还没获取到。
prev[i] = vs; // 顶点i的前驱顶点为0。
dist[i] = map[vs][i].weight; // 顶点i的最短路径为"顶点vs"到"顶点i"的权。
}
dist[vs] = 0,flag[vs] = 1; // 对"顶点vs"自身进行初始化
for (i = 0; i < VerNum - 1; i++) // 遍历1次;每次找出一个顶点的最短路径。
{ // 寻找当前最小的路径;即,在未获取最短路径的顶点中,找到离vs最近的顶点(k)。
min = INF;
for (j = 0; j < VerNum; j++)
{
if (flag[j]==0 && dist[j]<min)
{
min = dist[j];
k = j;
}
}
flag[k] = 1; // 标记"顶点k"为已经获取到最短路径
// 修正当前最短路径和前驱顶点: 即当已经"顶点k的最短路径"之后,更新"未获取最短路径的顶点的最短路径和前驱顶点"。
if(k==ve) return;
for (j = 0; j < VerNum; j++)
{
tmp = (map[k][j].weight==INF ? INF : (min + map[k][j].weight)); // 防止溢出
if (flag[j] == 0 && (tmp < dist[j]) && map[k][j].lineID>0)
{
dist[j] = tmp;
prev[j] = k; //记录前驱
}
}
}
}
void PrintPath(int v1,int v2)
{
int i,EdgeLast=v1,pathLen=1,u=path[top-1];//i是变量,边的起点,长度,边的终点
int lineId=map[EdgeLast][u].lineID; //开始路线编号
printf("%s-%d",StationID_list[v1].stationName,lineId); //打印起点站和起点站的路线
EdgeLast = u;
for(i=top-2;i>=0;i--) //利用栈倒过来寻找
{
u=path[i]; //更新终点
if(lineId != map[EdgeLast][u].lineID) //换乘
{
lineId = map[EdgeLast][u].lineID;
printf("(%d)-%s-%d",pathLen,StationID_list[EdgeLast].stationName,lineId);
pathLen=0;
}
pathLen++; //长度 +1
EdgeLast = u; //更新起点
}
printf("(%d)-%s",pathLen,StationID_list[v2].stationName);//打印终点站
}
Floyd
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define M 618
#define INF 0x3f3f3f3f
struct station{ //地铁站序号结构体
char stationName[30]; //站名
int IsChange; //能否换乘
};
struct vertex{ //地铁图结构体
int weight; //权重
int lineID; //路线序号
};
struct station StationID_list[M]; //地铁站序号数组
struct vertex map[M][M]; //地铁图
int lineID,StationNum,lineNum,IsChange,VerNum; //路线序号,一条路线中地铁站个数,路线个数,是否换乘,总地铁站个数
int prev[M],dist[M],path[M],top,pathID[M][M]; //跟踪数组,最短路径数值数组,dijkstra最短路径编号数组,栈顶,Floyd最短路径编号数组
char StationBegin[30],StationEnd[30]; //起点站,终点站
void DrawSubwayMap(FILE *fp); //建图
int SearchMap(char *s); //找站名是否出现过
void floyd(int v1,int v2); //floyd算法
void PrintPath(int v1,int v2); //打印路径
int main()
{
int i,j,v1,v2,t;
FILE *fp = fopen("bgstations.txt","r");
scanf("%s %s",StationBegin,StationEnd);
for(i=0;i<M;i++) //初始化图
for(j=0;j<M;j++)
{
map[i][j].weight=map[j][i].weight=INF; //权重无穷大
map[i][j].lineID=map[j][i].lineID=0; //编号为0
}
DrawSubwayMap(fp); //建图
v1=SearchMap(StationBegin); //找到起点站编号
v2=SearchMap(StationEnd); //找到终点站编号
floyd(v1,v2); //找最短路
for(t=v2;t!=v1;t=pathID[v1][t]) //路径追溯
{
path[top]=t;
top++;
}
PrintPath(v1,v2); //打印编号
return 0;
}
void DrawSubwayMap(FILE *fp)
{
int i,j,ContainID,EdgeLast;//两个变量,存在的地铁站的编号,边的起点
char stationName[30]; //站名
fscanf(fp,"%d",&lineNum);
for(i=0;i<lineNum;i++)
{
fscanf(fp,"%d %d",&lineID,&StationNum);
EdgeLast=-1; //每一条路线一开始都是 -1
for(j=0;j<StationNum;j++)
{
fscanf(fp,"%s %d",stationName,&IsChange);
ContainID=SearchMap(stationName); //看看有没有
if(ContainID == -1) //没有
{
strcpy(StationID_list[VerNum].stationName,stationName); //存储
StationID_list[VerNum].IsChange=IsChange; //存储
if(EdgeLast != -1) //如果有边的起点
{
map[EdgeLast][VerNum].lineID=map[VerNum][EdgeLast].lineID=lineID; //存储
map[EdgeLast][VerNum].weight=map[VerNum][EdgeLast].weight=1; //存储
}
EdgeLast=VerNum; //终点变起点
VerNum++; //总数 +1
}
else
{
if(EdgeLast != -1) //如果有边的起点
{
map[EdgeLast][ContainID].lineID=map[ContainID][EdgeLast].lineID=lineID;//存储
map[EdgeLast][ContainID].weight=map[ContainID][EdgeLast].weight=1; //存储
}
EdgeLast = ContainID; //终点变起点
}
}
}
}
int SearchMap(char *s)
{
int i;
for(i=0;i<VerNum;i++)
if(strcmp(s,StationID_list[i].stationName)==0)
return i; //返回序号
return -1;
}
void floyd(int v1,int v2)
{
int i,j,k;
for(i=0;i<VerNum;i++)
for(j=0;j<VerNum;j++)
if(i!=j && map[i][j].weight<INF)
pathID[i][j]=i; //初始化
for(k=0;k<VerNum;k++)
for(i=0;i<VerNum;i++)
for(j=0;j<VerNum;j++)
if(map[i][j].weight>map[i][k].weight+map[k][j].weight) //三角形原则更新路径
{
map[i][j].weight=map[i][k].weight+map[k][j].weight;
pathID[i][j]=pathID[k][j]; //记录编号
}
}
void PrintPath(int v1,int v2)
{
int i,EdgeLast=v1,pathLen=1,u=path[top-1];//i是变量,边的起点,长度,边的终点
int lineId=map[EdgeLast][u].lineID; //开始路线编号
printf("%s-%d",StationID_list[v1].stationName,lineId); //打印起点站和起点站的路线
EdgeLast = u;
for(i=top-2;i>=0;i--) //利用栈倒过来寻找
{
u=path[i]; //更新终点
if(lineId != map[EdgeLast][u].lineID) //换乘
{
lineId = map[EdgeLast][u].lineID;
printf("(%d)-%s-%d",pathLen,StationID_list[EdgeLast].stationName,lineId);
pathLen=0;
}
pathLen++; //长度 +1
EdgeLast = u; //更新起点
}
printf("(%d)-%s",pathLen,StationID_list[v2].stationName);//打印终点站
}
只有换乘站和起点终点站构图(即忽略中间站)的题解。本题解由2073 陶索梓(网名,不是真名)大哥提供
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
int line,lm[30];
char ssn[210],esn[210];
char zhan[34][80][210];
int opr[34][100];
char name[400][400],t=1;
int weight[400][400];
int path[400][400];
int line_name[35];
int spath[400];
int sweight[400],wfound[400];
void init() {
int i,j;
for(i=0;i<=t;i++) {
for(j=0;j<=t;j++) {
weight[i][j]=0x3f3f3f3f;
}
}
}
void Dijkstra(int v0){
int i,j,v,minweight;
for(i=0;i<=t;i++) {
sweight[i] = weight[v0][i];
spath[i] = v0;
}
sweight[v0] = 0;
wfound[v0] = 1;
for(i=0;i<t;i++) {
minweight=1e9;
v=-1;
for(j=0;j<=t;j++) {
if(!wfound[j]&&(sweight[j]<minweight)){
v=j;
minweight=sweight[v];
}
}
if(v==-1){
return;
}
wfound[v]=1;
for(j=0;j<=t;j++) {
if(!wfound[j]&&(minweight+weight[v][j]<sweight[j])){
sweight[j]=minweight+weight[v][j];
spath[j]=v;
}
}
}
}
void insert(char s[],int i,int j) {
int k;
for(k=0;k<=t;k++) {
if(strcmp(name[k],s)==0) {
return;
}
}
strcpy(name[t++],zhan[i][j]);
return;
}
int find_name(char s[]) {
int i;
for(i=0;i<=t;i++){
if(strcmp(s,name[i])==0) {
return i;
}
}
}
void add(int u,int v,int d,int id) {
//printf("ADD:%d %d %d站 %d号线n",u,v,d,id);
if(weight[u][v]>d) {
weight[u][v]=weight[v][u]=d;
path[u][v]=path[v][u]=id;
}
}
int main() {
FILE *in;
in=fopen("bgstations.txt","r");
scanf("%sn%s",ssn,esn);
fscanf(in,"%d",&line);
/*if(strcmp(ssn,"动物园")==0&&strcmp(esn,"北京南站")==01) {
printf("动物园-4(1)-西直门-2(5)-宣武门-4(3)-北京南站");
return 0;
}*/
int i,j,k,ssni,ssnj;
for(i=1;i<=line;i++) {
fscanf(in,"%d %d",&line_name[i],&lm[i]);
for(j=1;j<=lm[i];j++) {
fscanf(in,"%s %d",zhan[i][j],&opr[i][j]);
if(strcmp(zhan[i][j],esn)==0) {
strcpy(name[0],esn);
opr[i][j]=1;
}else if(strcmp(zhan[i][j],ssn)==0) {
opr[i][j]=1;
ssni=i;ssnj=j;
}else if(opr[i][j]==1) {
insert(zhan[i][j],i,j);
//strcpy(name[t++],zhan[i][j]);
}
}
}
strcpy(name[t],zhan[ssni][ssnj]);
//printf("n");
//for(i=0;i<=t;i++) {
//printf("%d %sn",i,name[i]);
//}
init();
for(i=1;i<=line;i++) {
int fir,pre=-1;
for(j=1;j<=lm[i];j++) {
if(opr[i][j]==1) {
if(pre!=-1) {
int u,v;
u= find_name(zhan[i][pre]);
v=find_name(zhan[i][j]);
add(u,v,j-pre,line_name[i]);
pre=j;
}else {
fir=pre=j;
}
}
}
if(strcmp(zhan[i][1],zhan[i][lm[i]])==0&&lm[i]+fir!=1+pre) {
int u,v;
u= find_name(zhan[i][pre]);
v=find_name(zhan[i][fir]);
if(u!=v) {
//printf("!!n");
add(u,v,fir-1+lm[i]-pre,line_name[i]);
}
}
}
Dijkstra(0);
//printf("%s",name[t]);
int q=t;
char ans_name[300][300];
int ans_path[300];
int ans_weight[300];
int anstop=0;
while(q!=0) {
strcpy(ans_name[anstop],name[q]);
ans_path[anstop]=path[q][spath[q]];
ans_weight[anstop]=weight[q][spath[q]];
anstop++;
//printf("%s-%d(%d)-",name[q],path[q][spath[q]],weight[q][spath[q]]);
q=spath[q];
}
for(i=0;i<anstop;i++) {
if(ans_path[i]==ans_path[i-1]) {
ans_weight[i-1]+=ans_weight[i];
for(j=i+1;j<anstop;j++) {
strcpy(ans_name[j-1],ans_name[j]);
ans_path[j-1]=ans_path[j];
ans_weight[j-1]=ans_weight[j];
}
anstop--;
i--;
}
}
for(i=0;i<anstop;i++) {
printf("%s-%d(%d)-",ans_name[i],ans_path[i],ans_weight[i]);
}
printf("%s",name[0]);
fclose(in);
return 0;
}
补充测试的数据
以下的输入输出是基于我们手头上有的txt文档给出的结果
【样例输入输出】
北京大学东门 天安门东
北京大学东门-4(2)-海淀黄庄-10(2)-知春路-13(2)-西直门-2(3)-复兴门-1(3)-天安门东
【样例输入输出】
苹果园 天通苑北
苹果园-1(8)-军事博物馆-9(2)-白石桥南-6(2)-车公庄-2(1)-西直门-13(9)-立水桥-5(3)-天通苑北
【样例输入输出】
海淀黄庄 车道沟
海淀黄庄-10(5)-车道沟
【样例输入输出】
海淀黄庄 鼓楼大街
海淀黄庄-10(2)-知春路-13(2)-西直门-2(2)-鼓楼大街
【样例输入输出】
长椿街 芍药居
长椿街-2(8)-雍和宫-5(3)-惠新西街南口-10(1)-芍药居
(长椿街-2(9)-东直门-13(3)-芍药居)
(长椿街-2(6)-鼓楼大街-8(3)-北土城-10(3)-芍药居)
【样例输入输出】
安河桥北 善各庄
安河桥北-4(6)-海淀黄庄-10(9)-芍药居-13(1)-望京西-15(1)-望京-14(3)-善各庄
【样例输入输出】
苹果园 国贸
苹果园-1(19)-国贸
【样例输入输出】
清华东路西口 海淀五路居
清华东路西口-15(3)-奥林匹克公园-8(5)-鼓楼大街-2(2)-西直门-4(2)-国家图书馆-9(1)-白石桥南-6(3)-海淀五路居
(清华东路西口-15(3)-奥林匹克公园-8(5)-鼓楼大街-2(3)-车公庄-6(5)-海淀五路居)
【样例输入输出】
永安里 东大桥
永安里-1(1)-建国门-2(1)-朝阳门-6(1)-东大桥
以下的输入输出是自行输入txt文档给出的结果
输入:
动物园
北京南站
输出:
动物园-4(1)-西直门-2(5)-宣武门-4(3)-北京南站
bgstations.txt:
2
2 19
西直门 1
积水潭 0
鼓楼大街 0
安定门 0
雍和宫 0
东直门 0
东四十条 0
朝阳门 0
建国门 0
北京站 0
崇文门 0
前门 0
和平门 0
宣武门 1
长椿街 0
复兴门 0
阜成门 0
车公庄 0
西直门 1
4 24
安河桥北 0
北宫门 0
西苑 0
圆明园 0
北京大学东门 0
中关村 0
海淀黄庄 0
人民大学 0
魏公村 0
国家图书馆 0
动物园 0
西直门 1
新街口 0
平安里 0
西四 0
灵境胡同 0
西单 0
宣武门 1
菜市口 0
陶然亭 0
北京南站 0
马家堡 0
角门西 0
公益西桥 0
最短路径算法小拓
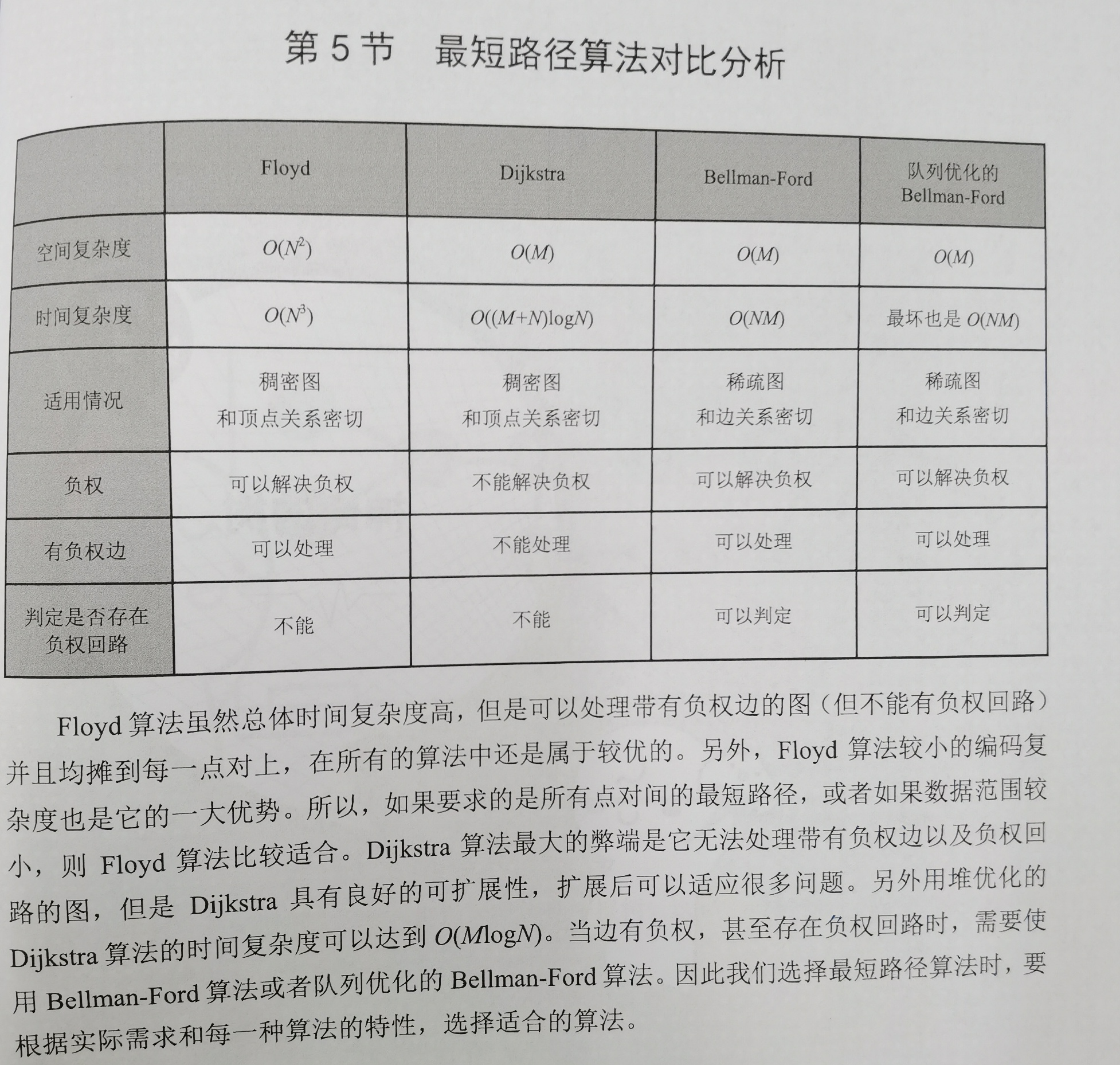
对于负权边,Dijkstra不能用,只能用Floyd或Belman-Ford
关于优化,Floyd最暴力很难优化,Dijkstra可以用优先队列优化(上图Dijkstra的时间复杂度为优化之后的),Belman-Ford也可以用队列优化。查找还可以使用Hash优化。
综上所述,Belman-Ford很不错,但是因其时间复杂度在图比较复杂的时候较高而不常使用,倒是有一个队列优化的算法SPFA经常使用,但是这个算法在某些奇怪的情况下(比如菊花图)时间复杂度会退化成最差的时间复杂度(算法竞赛有时候会卡SPFA),但是这个题目我测试过,SPFA目前是最快的哈哈哈哈(但是我懒得写了)
最后
以上就是无心衬衫最近收集整理的关于BUAA(2021春) 北京地铁乘坐线路查询——Dijkstra和Floyd双解法看前须知第七次上机题汇总题目内容题解的全部内容,更多相关BUAA(2021春)内容请搜索靠谱客的其他文章。








发表评论 取消回复