【图像处理】图像处理算子

66 阅读 0 评论 44 点赞

我是靠谱客的博主可耐飞机，最近开发中收集的这篇文章主要介绍【图像处理】图像处理算子，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

学习使用不同的滤波器对图像进行处理
前言：以下内容是笔者学习过程中的归纳终结，以便日后复习，如有侵权，联系删除。

一、常见滤波算子

一、均值滤波
这是由一个归一化卷积框完成的。他只是用卷积框覆盖区域所有像素的平均值来代替中心元素。可以使用函数 cv2.blur() 和 cv2.boxFilter() 来完这个任务。可以同看查看文档了解更多卷积框的细节。我们需要设定卷积框的宽和高。下面是一个 3x3 的归一化卷积框：
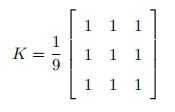
在这里插入图片描述

import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('opencv_logo.png')
blur = cv2.blur(img,(5,5))
plt.subplot(121),plt.imshow(img),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(blur),plt.title('Blurred')
plt.xticks([]), plt.yticks([])
plt.show()

在这里插入图片描述
二、高斯滤波
现在把卷积核换成高斯核（简单来说，方框不变，将原来每个方框的值是相等的，现在里面的值是符合高斯分布的，方框中心的值最大，其余方框根据距离中心元素的距离递减，构成一个高斯小山包。原来的求平均数现在变成求加权平均数，全就是方框里的值）。实现的函数是 cv2.GaussianBlur()。我们需要指定高斯核的宽和高（必须是奇数）。以及高斯函数沿 X，Y 方向的标准差。如果我们只指定了 X 方向的的标准差，Y 方向也会取相同值。如果两个标准差都是 0，那么函数会根据核函数的大小自己计算。高斯滤波可以有效的从图像中去除高斯噪音。高斯公式：
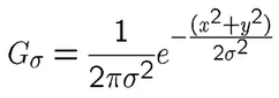
在这里插入图片描述
如果你愿意的话，你也可以使用函数cv2.getGaussianKernel() 自己构建一高斯核。如果要使用高斯模糊的话，上边的代码应该写成：

#0 是指根据窗口大小（5,5）来计算高斯函数标准差
blur = cv2.GaussianBlur(img,(5,5),0)

在这里插入图片描述
三、中值滤波
顾名思义就是用与卷积框对应像素的中值来替代中心像素的值。这个滤波器经常用来去除椒盐噪声。前面的滤波器都是用计算得到的一个新值来取代中心像素的值，而中值滤波是用中心像素周围（也可以使他本身）的值来取代他。他能有效的去除噪声。卷积核的大小也应该是一个奇数。在这个例子中，我们给原始图像加上 50% 的噪声然后再使用中值模糊。

median = cv2.medianBlur(img,5)

在这里插入图片描述

二、图像梯度

• 图像梯度，图像边界等
• 使用到的函数有：cv2.Sobel()，cv2.Schar()，cv2.Laplacian() 等梯度简单来说就是求导。OpenCV 提供了三种不同的梯度滤波器，或者说高通滤波器：Sobel，Scharr 和 Laplacian。我会一一介绍他们。Sobel，Scharr 其实就是求一阶或二阶导数。Scharr 是对 Sobel（使用小的卷积核求解求解梯度角度时）的优化。Laplacian 是求二阶导数。
一、Sobel 算子和 Scharr 算子
Sobel 算子是高斯平滑与微分操作的结合体，所以它的抗噪声能力很好。你可以设定求导的方向（xorder 或 yorder）。还可以设定使用的卷积核的大小（ksize）。如果 ksize=-1，会使用 3x3 的 Scharr 滤波器，它的的效果要比 3x3 的 Sobel 滤波器好（而且速度相同，所以在使用 3x3 滤波器时应该尽量使用 Scharr 滤波器）。3x3 的 Sobel 滤波器卷积核如下：
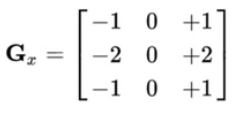
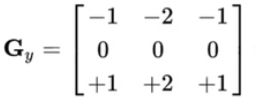
在这里插入图片描述
3x3 的 Scharr 滤波器卷积核如下：

二、 Laplacian 算子
拉普拉斯算子可以使用二阶导数的形式定义，可假设其离散实现类似于二阶 Sobel 导数，事实上，OpenCV 在计算拉普拉斯算子时直接调用 Sobel 算子。计算公式如下：
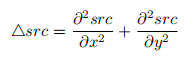
在这里插入图片描述
拉普拉斯滤波器使用的卷积核：

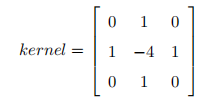
下面的代码分别使用以上三种滤波器对同一幅图进行操作。使用的卷积核都是 5x5 的。

import cv2
import numpy as np
from matplotlib import pyplot as plt
img=cv2.imread('dave.jpg',0)
#cv2.CV_64F 输出图像的深度（数据类型），可以使用-1, 与原图像保持一致 np.uint8
laplacian=cv2.Laplacian(img,cv2.CV_64F)
# 参数 1,0 为只在 x 方向求一阶导数，最大可以求 2 阶导数。
sobelx=cv2.Sobel(img,cv2.CV_64F,1,0,ksize=5) # 参数 0,1 为只在 y 方向求一阶导数，最大可以求 2 阶导数。
sobely=cv2.Sobel(img,cv2.CV_64F,0,1,ksize=5)
plt.subplot(2,2,1),plt.imshow(img,cmap = 'gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,2),plt.imshow(laplacian,cmap = 'gray')
plt.title('Laplacian'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,3),plt.imshow(sobelx,cmap = 'gray')
plt.title('Sobel X'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,4),plt.imshow(sobely,cmap = 'gray')
plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])
plt.show()

结果：
在这里插入图片描述

三、边缘检测

这里主要介绍Canny边缘检测，Canny 边缘检测是一种非常流行的边缘检测算法，是 John F.Canny 在1986 年提出的。它是一个有很多步构成的算法，我们接下来会逐步介绍。先看看具体步骤：
1.由于边缘检测很容易受到噪声影响，所以第一步是使用高斯滤波器去除噪声。
2.对平滑后的图像使用 Sobel 算子计算水平方向和竖直方向的一阶导数（图像梯度）（Gx 和 Gy）。根据得到的这两幅梯度图（Gx 和 Gy）找到边界的梯度大小和方向，公式如下：
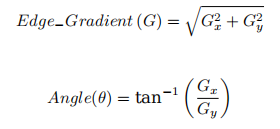
在这里插入图片描述
3.非极大值抑制
在获得梯度的方向和大小之后，应该对整幅图像做一个扫描，去除那些非边界上的点。对每一个像素进行检查，看这个点的梯度是不是周围具有相同梯度方向的点中最大的。如下图所示：

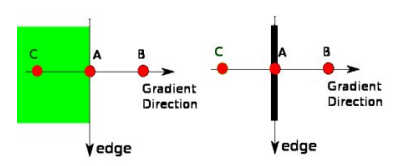
假设B、C点是A点梯度方向上的两个点，如果A点的梯度大小比B、C都大，则A会视为边界点保留。
4.滞后阈值
现在要确定哪些边界才是真正的边界。这时我们需要设置两个阈值：minVal 和 maxVal。当图像的灰度梯度高于 maxVal 时被认为是真的边界，那些低于 minVal 的边界会被抛弃。如果介于两者之间的话，就要看这个点是否与某个被确定为真正的边界点相连，如果是就认为它也是边界点，如果不是就抛弃。如下图：
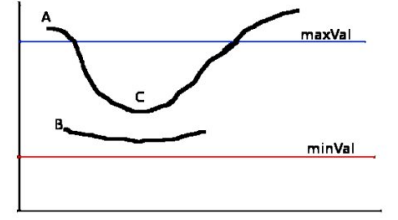
在这里插入图片描述
A 高于阈值 maxVal 所以是真正的边界点，C 虽然低于 maxVal 但高于minVal 并且与 A 相连，所以也被认为是真正的边界点。而 B 就会被抛弃，因为他不仅低于 maxVal 而且不与真正的边界点相连。所以选择合适的 maxVal和 minVal 对于能否得到好的结果非常重要。
代码：
在 OpenCV 中只需要一个函数：cv2.Canny()，就可以完成以上几步。让我们看如何使用这个函数。这个函数的第一个参数是输入图像。第二和第三个分别是 minVal 和 maxVal。第三个参数设置用来计算图像梯度的 Sobel卷积核的大小，默认值为 3。最后一个参数是 L2gradient，它可以用来设定求梯度大小的方程，默认值为 False。

import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('messi5.jpg',0)
edges = cv2.Canny(img,100,200)
plt.subplot(121),plt.imshow(img,cmap = 'gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(edges,cmap = 'gray')
plt.title('Edge Image'), plt.xticks([]), plt.yticks([])
plt.show()