高尔顿钉板概率模型的实现

53 阅读 0 评论 35 点赞

我是靠谱客的博主儒雅发箍，最近开发中收集的这篇文章主要介绍高尔顿钉板概率模型的实现，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

高尔顿钉板是一个关于概率的模型，小球每次下落，将随机的向两边等概率的下落，当有大量的小球都滚下时，最终在钉板下面不同位置收集到的小球数量，将符合二项分布概率。

出于兴趣，在VC编译环境下，通过C++语言，模拟实现了高尔顿钉板的概率模型。本程序中定义了两个类，Ball和Holder类，Ball 是定义的小球类，Holder是定义的钉板类。Holder类主要负责画图显现模板框架，以及当一个小球滚到钉板下面容器位置，将小球放在合适的位置，并且当整个容器满的时候，即停止程序运行。小球类，定义了小球所处位置，并对小球进行作图。另外定义了根据传入的参数的移动规则，即，向左或者向右移动。另外定义了一个control函数，来控制holder和Ball类对象之间的交互，并且达到动态效果

。

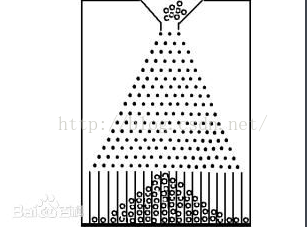
图1 高尔顿钉板模型

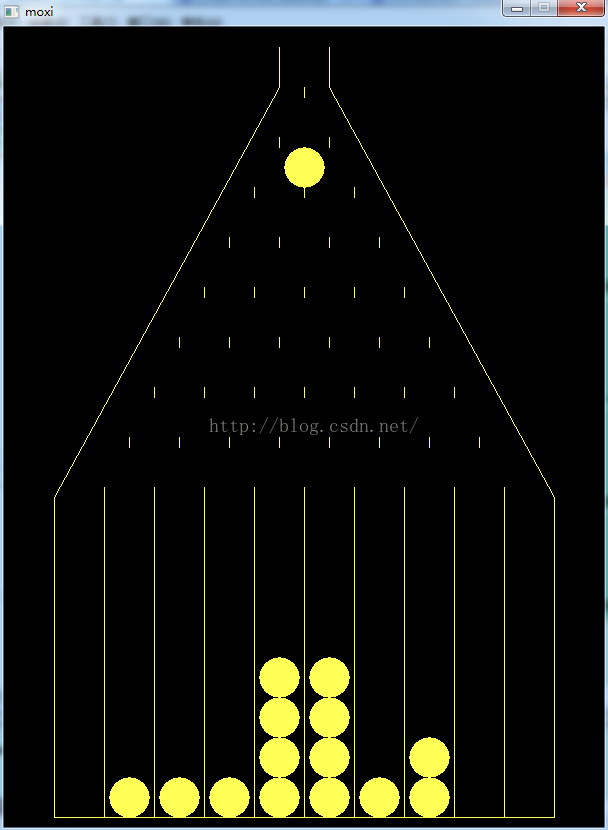
图 2 程序运行图1 图3 程序运行图2

源代码：

#include <graphics.h>
#include <conio.h>
#include <math.h>
#include "iostream"

class Ball
{
public:
Ball()
{
x=300;
y=40;
flag=1;
}
int getX()
{
return x;
}
int getY()
{
return y;
}
int getFlag()
{
return flag;
}
int move(int i);
void fixed(int y1);
void draw()
{
solidcircle(x,y,20);
}

private:
int x,y;
int flag;
int level;
};

class Holder
{
public:
Holder()
{
for(int i=0;i<10;i++)
for(int j=0;j<7;j++)
a[i][j]=0;
full=0;
}
void draw();
int getfull()
{
return full;
}
void steady_one(Ball &b);
private:
int a[10][7];
int full;
};
void Holder::steady_one(Ball &b)
{
int i=0,temp=0;
if(b.getFlag()==0 && full==0)
{
temp = b.getX()-50-25;
temp=temp/50;
for(i=0;i<7;i++)
{
if(a[temp][i]==0)
{
a[temp][i]=1;
b.fixed(790-i*40-20);
break;
}

}
}
for(i=0;i<10;i++)
{
if(a[i][6]==1)
{
full=1;
break;
}
}
}
void Holder::draw()
{
int i=0,j=0,tempx=100,tempy=460;
line(50,790,550,790);
for(i=0;i<11;i++)
{
line(50+i*50,470,50+i*50,790);
}
for(i=9;i>0;i--,tempx += 25,tempy -= 50)
for(j=0;j<i;j++)
{
line(tempx+j*50,tempy,tempx+j*50,tempy+10);
}
line(275,60,275,20);
line(325,60,325,20);
line(275,60,50,470);
line(325,60,550,470);
}

int Ball::move(int i)
{
if(i==0)
{
if(flag==1)
{
x -= 25;
y += 50;
if(y>470)
{
flag=0;
}
}
}
else if(i==1)
{
if(flag==1)
{
x += 25;
y += 50;
if(y>470)
flag=0;
}
}
return 0;
}
void Ball::fixed(int y1)
{
y=y1;
}
int control()
{
Holder h1;
Ball b[50];
int num=1,i=0,temp,c[50];
for(i=0;i<50;i++)
c[i]=1;
while(1)
{
for(i=0;i<num;i++)
{
if(c[i]==1)
{
if(b[i].getFlag()==1)
{
temp=rand()%2;
b[i].move(temp);
}
else
{
h1.steady_one(b[i]);
num++;
c[i]=0;
}
}
}
h1.draw();
for(i=0;i<num;i++)
b[i].draw();
if(h1.getfull()==1)
break;
Sleep(300);
cleardevice();
}
return 0;
}
int main()
{
initgraph(600, 800);
setcolor(YELLOW);
setfillcolor(YELLOW);
control();
Sleep(10000);
return 0;
}