矩阵向量范数
我们说行列式是对矩阵变换的整体一个度量,比如他等于特征值的乘积(特征空间的体积)等等性质都能表明他确实是一个度量。我们还需要其他的度量诸如矩阵非方阵时,这种整体“大小”的度量有利于描述扰动的大小和灵敏度的分析参见《数值分析》。也有利于在优化和机器学习中起到正则化约束的作用,可以看作是矩阵或者向量距离的测度,这就是【范数】
用记号||.||表示范数。
向量范数
自然,我们会想到怎样定义范数?我们先给出他应当满足的性质:
- 正定,即 ∣ ∣ x ∣ ∣ > = 0 ||x||>=0 ∣∣x∣∣>=0当且仅当x=0等号成立
- 齐次, ∣ k x ⃗ ∣ = ∣ k ∣ ∣ x ⃗ ∣ |kvec{x}|=|k||vec{x}| ∣kx∣=∣k∣∣x∣
- 三角不等(几何属性),
∣
x
+
y
∣
<
=
∣
x
∣
+
∣
y
∣
|x+y|<=|x|+|y|
∣x+y∣<=∣x∣+∣y∣
其中,一个常用的p范数(holder范数)就是一个满足的例子:
∣ x ∣ p = ( ∣ x 1 ∣ p + ∣ x 2 ∣ p + . . . ∣ x n ∣ p ) 1 / p |x|_p=(|x_1|^p+|x_2|^p+...|x_n|^p)^{1/p} ∣x∣p=(∣x1∣p+∣x2∣p+...∣xn∣p)1/p
特别的对于p=1 2,inf说最常用的: ∣ x ∣ 1 = ∑ i n ∣ x i ∣ , ∣ x ∣ 2 = s q r t ( ∑ i n ∣ x i ∣ 2 ) , ∣ x ∣ ∞ = m a x i ∣ x i ∣ |x|_1=sum_i^n|x_i|,|x|_2=sqrt(sum_i^n|x_i|^2),|x|_{infty}=max_i|xi| ∣x∣1=∑in∣xi∣,∣x∣2=sqrt(∑in∣xi∣2),∣x∣∞=maxi∣xi∣
L1对应着绝对值求和;L2对应着平方和的平方根;Linf对应绝对值最大的分量
另外,无论我们引入了什么形式的范数,范数都满足如下两个定理:- 任意两个范数$|.|{alpha},|.|{beta}对任意x必定存在c1|x|
我们可以观察范数p取不同值时的二维图形:
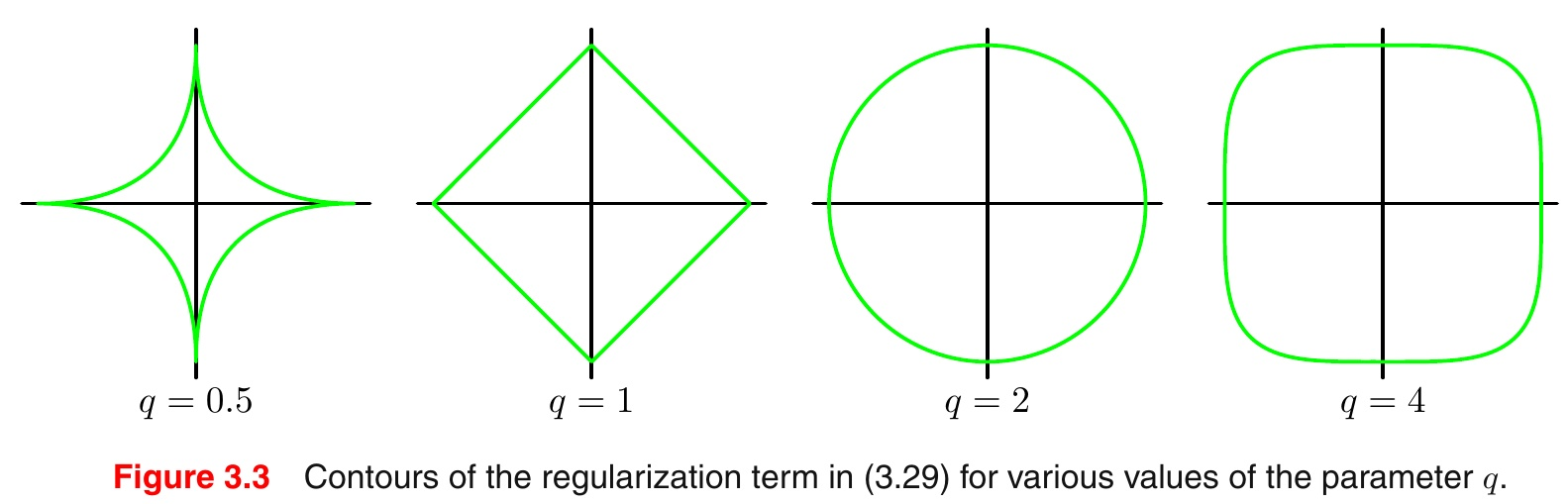
特别地:
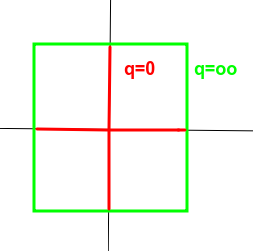
- 任意两个范数$|.|{alpha},|.|{beta}对任意x必定存在c1|x|
矩阵范数
同样的矩阵范数我们也应当让他满足上面三个性质,之外我们再附加一个性质:
相容性,|A||B|>=|AB|
而且有
∣
A
x
⃗
∣
<
=
∣
A
∣
∣
x
⃗
∣
|Avec{x}|<=|A||vec{x}|
∣Ax∣<=∣A∣∣x∣即矩阵范数和向量范数时相容的
那么什么样的数学形式能满足4个条件呢?
定义||A||=
m
a
x
∣
A
x
⃗
∣
,
∣
x
∣
=
1
max|Avec{x}|,|x|=1
max∣Ax∣,∣x∣=1就是满足条件的一个矩阵范数(证明略去)
上面的矩阵范数定义称之为从属于向量范数的矩阵范数,也称之为【算子范数】,对应的矩阵范数如下:
∣
A
∣
p
=
m
a
x
:
∣
A
x
⃗
∣
p
,
∣
x
∣
=
1
∣
|A|_p=max:|Avec{x}|_p,|x|=1|
∣A∣p=max:∣Ax∣p,∣x∣=1∣
特别的对于p=1,2,inf,分别对应着,列绝对值和最大,行绝对值和最大,
A
T
A
A^TA
ATA最大特征值的平方根也叫【谱范数】
显然还有其他满足我们性质的范数定义和性质,这里就不列出来了,这不是我写的目的。包括什么【谱半径】之类的,很明显就是矩阵最大特征值的绝对值,显然谱半径类似于无穷级数的半径其远大于1表明了某种矩阵幂的不收敛。这会在之后的数值分析和矩阵算法详细讨论。
机器学习中的几个向量范数[1,2]
知乎给出了机器学习正则约束的一篇简单介绍见[1]另外一篇有些冗长的[2]。
机器学习中有很多关于欠拟合与过拟合,模型简单还是复杂等的讨论,这里不多言,直接看一个加了正则项惩罚项的处理例子。
首先看常见的一个拟合例子:
m
i
n
:
1
N
∑
i
N
l
o
s
s
(
y
i
,
f
(
x
i
)
)
+
λ
J
(
θ
)
min:frac{1}{N}sum_i^Nloss(yi,f(xi))+lambda J(theta)
min:N1i∑Nloss(yi,f(xi))+λJ(θ)
简单情况就是线性拟合:
f
=
θ
T
x
f=theta^Tbm{x}
f=θTx且loss采用均方误差。
0. 当没有后面的正则约束项时结果为
θ
=
(
X
T
X
)
−
1
X
T
y
=
X
+
y
theta=(X^TX)^{-1}X^Ty=X^+y
θ=(XTX)−1XTy=X+y
- 当惩罚函数J取L2范数时(最小二乘)
θ = ( X T X + λ I ) − 1 X T y theta=(X^TX+lambda I)^{-1}X^Ty θ=(XTX+λI)−1XTy
当数据比样本维度还高时,XTX也未必可逆,即他是【病态的】,【条件数很大】此时我们可以用近似的方法如SGD迭代
求近似的逆,但更多的时候我们是加入了二范数的正则项如上式,可以看到速度会比SGD更快,而且正则项在控制方差与
偏差,过拟合,模型是否简单上的权衡更好,泛华能力更强。他也是等价于GPR的贝叶斯回归。这里还能看到这个形式和
高斯过程回归的方差矩阵很想,这里的lambda和那里的噪声都sigma是等效的,起到保证可逆的数值稳定作用,同时又防
止了过拟合,还起到平滑的作用。
由于二次型惩罚函数像一个岭故这就是【岭回归】 - 当惩罚函数J为L1范数时
即 J ( θ ) = ∣ θ ∣ 1 J(theta)=|theta|_1 J(θ)=∣θ∣1原目标式为 m i n : ∣ y − θ T x ∣ + λ θ ∣ 1 min:|y-theta^Tx|+lambdatheta|_1 min:∣y−θTx∣+λθ∣1
这也对应称之为【lasso回归】 - 两者比较
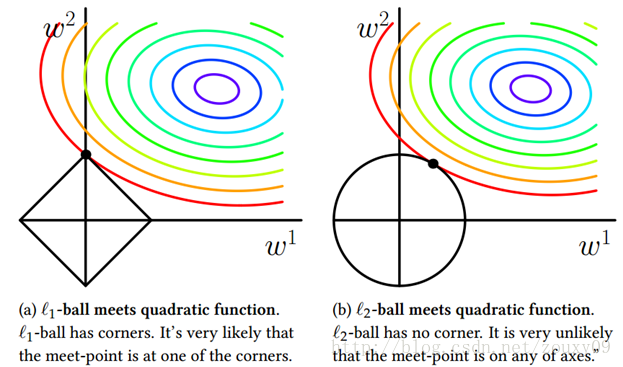
图中等高线圈表示可行的解范围,黑线表示范数约束。显然最优的解是两者刚好相切(PRML)。可以看到L1范数的切点解能在坐标轴上,L2范数不行。这意味着L1范数代表着【稀疏化】,即参数w或者说是 θ theta θ的很多分量会为0.这样纸就表明求解出来的参数结果会很简单而且自带特征提取和降维的效果,更好的解释性(即向客户解释哪些是主要因素主要特征),因为他把一些不重要的维度0了。二范式L2显然不行,他只会让整个参数W接近于0但不会平衡各个分量。
因此也就等效的得出岭回归和lasso回归的优劣:lasso回归有特征选取倾向于减少特征但是计算复杂不便于求解,L1不可连续导;岭回归倾向于选择更多的特征,预测解释性不强 - L0范数
那有人会问,既然范数越接近坐标轴越稀疏为什么不选L0呢这个更接近坐标更稀疏,因为这更难求解是NP问题
范数与特征选取[3]
前面说到范数具有稀疏化和特征选取的作用,有NIPS一篇论文就是基于此做的特征值的选取可以参考
[3]Feiping Nie, Heng Huang, Xiao Cai, Chris H. Q. Ding. Efficient and Robust Feature Selection via Joint L2,1-Norms Minimization,NIPS,pp.1813-1821, 2010
迹
目前没有想到很好地几何等直观解释,只能说这种对角和等于特征值和很奇妙。也表明了某种度量。tr()有很多性质所以在机器学习里面尤其是矩阵求导里特别有用,很多技巧在程序中也很有用。
一篇较简单的知乎讨论[1]https://www.zhihu.com/question/20473040
一篇稍显冗长的小白贴[2]https://blog.csdn.net/zouxy09/article/details/24971995
[3]一篇中文的解读https://blog.csdn.net/lqzdreamer/article/details/79678875有时间再来补充下本篇博文,博文不是讲数学而是重新认识数学,解读数学意义作用!
最后
以上就是痴情画笔最近收集整理的关于2.2 范数 迹矩阵向量范数迹的全部内容,更多相关2.2内容请搜索靠谱客的其他文章。








发表评论 取消回复