1. 高斯模型与高维高斯模型介绍
高斯模型也就是正态分布模型,该模型最早可见于我们的高中数学教材中。闻其名知其意,正态分布是自然界中普遍存在的一种分布。比如,考试成绩,人的智力水平等等。都是大致呈现为正态分布。其概率密度函数为
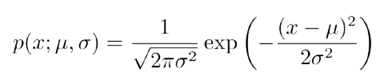
其中参数为μ,σ2 ,都是一维标量。
对于高维高斯模型,与一维类似,只是自变量变成了多维,是一个向量。其概率密度函数为
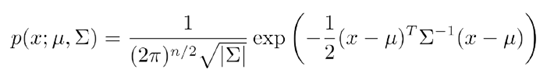
其中参数为μ,Σ , μ是向量,Σ是协方差矩阵,是个对称阵。
2. 高斯混合模型
高斯混合模型简单的说就是多个高斯模型的叠加。比如在某一个班级中,将男生和女生分成两个高斯模型来分别表示男生和女生的身高,将这个两个模型叠加到一起就是整个班级的高斯混合模型。然后此时,班上突然新来了一位同学,但是不知道ta是男生还是女生。这时首先就要对ta性别进行估计,假设有0.6的概率是男生,那么就是0.4的概率为女生。那么,对该同学的身高估计=0.6 班上男生(其中一个高斯分布)身高期望+0.4
班上女生(其中另一个高斯分布)身高期望。对于这个0.6是我们随意假设的,但是在大多数实际情况中,我们是不能直接得到其具体值的,也就是所谓的隐变量(latent variable)。而人的身高,是我们可以观察到的样本,也就是可观察变量(observed variable)。
下面用具体符号来说明。假设一共有K个高斯分布,获得每一个高斯分布的概率为,那么高斯混合分布模型如下
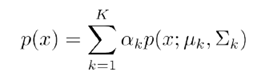
现在我们已知的是很多可观察样本(也就是一群人的身高,但是不知道性别),我们要来估计(也就是来估计属于男生和女生概率,男生高斯分布的两个参数和女生高斯分布的两个参数)。
我们用极大似然估计来估计模型参数,似然函数为
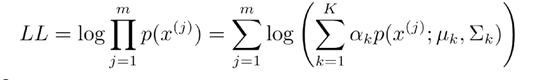
其中,一共有m个样本,![]() 表示第j个样本。我们的目标是求似然函数LL最大时的参数,一般情况下在这里直接对似然函数对参数求偏导即可。但是由于这里log里是一个求和式子,使得求导不能直接算出对应的参数取值。我们需要使用下面的方法来求解参数。
表示第j个样本。我们的目标是求似然函数LL最大时的参数,一般情况下在这里直接对似然函数对参数求偏导即可。但是由于这里log里是一个求和式子,使得求导不能直接算出对应的参数取值。我们需要使用下面的方法来求解参数。
3. EM算法来估计高斯混合模型的参数
EM算法的大致流程是这样的,先随机初始化原模型参数,由于不能通过求导算出对应的解析解,所以我们先得到某个LL函数的下界函数H,使得LL>=H,然后通过对相应变量求偏导算出使得H最大的相应参数值,将模型的参数更新为新求得的参数。此时模型参数改变,LL函数也改变,LL的下界H也需要改变,从新计算H函数后,又求导算出使得新的H最大的对应的参数值,又将参数更新,继续上述过程,直到收敛。
根据初始化的模型参数,我们可以根据贝叶斯公式求得第j个样本![]() 是来自第k个高斯分布产生的后验概率
是来自第k个高斯分布产生的后验概率
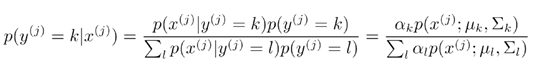
![]()
根据初始化参数算出的![]() 是已知的概率值,没有任何参数。根据上式可得
是已知的概率值,没有任何参数。根据上式可得
然后我们对LL函数作如下推导
由于log函数是上凸函数,根据Jensen不等式可以求出其下界。这里log函数里是一些项的乘积形式,求导求解比较方便。我们令
,然后分别对
求导,并令结果为0,分别解出
的相应的值。(PS. 在H函数中只有
是变量,其余都已知)。其中特别一点的是,求
时,由于
是有限制的,
,需要使用拉格朗日乘数法来计算。这里直接给出求解结果,具体求解步骤见附录。
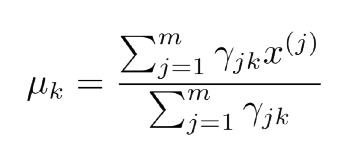
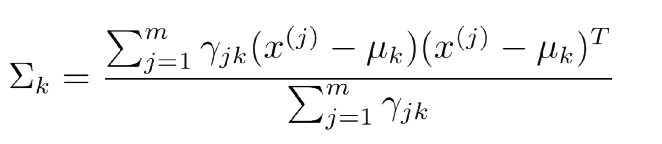
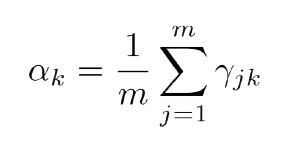
总结一下,完整的算法过程如下

4 代码
def Expectation(data, mu, sigma, alpha, K):
"""
EM算法的E步
:param data:数据集
:param mu:均值向量
:param sigma:协方差矩阵
:param alpha:混合系数
:return:各混合成分生成的后验概率gamma
"""
m = data.shape[0] #m为样本数量
#初始化后验概率矩阵gamma
gamma = np.zeros((m, K))
#计算各模型中所有样本出现的概率,行对应样本,列对应模型
prob = np.zeros((m, K))
for k in range(K):
prob[:, k] = alpha[k] * mul_normal(data, mu[k], sigma[k])
gamma = prob / np.sum(prob, axis=1, keepdims=True)
return gamma
def Maximization(data, gamma, K):
"""
更新模型参数
:param data:数据集
:param gamma:各混合成分生成的后验概率
:return:更新后的模型参数
"""
m, n = data.shape #m为样本数,n为特征数
#初始化高斯混合分布的模型参数值,因为要更新它们
mu = np.zeros((K, n))
sigma = []
mk = np.sum(gamma, axis=0)
#更新每个高斯混合成分的模型参数
for k in range(K):
#更新mu
mu[k, :] = gamma[:, k].reshape(1, m) * data / mk[k]
#更新sigma
sigma_k = (data - mu[k]).T * np.multiply((data - mu[k]), gamma[:, k].reshape(m, 1)) / mk[k]
sigma.append(sigma_k)
#更新alpha
alpha = mk / m
sigma = np.array(sigma) #为了保持一致,还需将sigma转回array
return mu, sigma, alpha
def GMM_EM(data, K, iterations):
"""
高斯混合聚类算法
:param data:数据集
:param K:簇数量
:param iterations:迭代次数
:return:
"""
mu, sigma, alpha = init_parameters(data, K)
for i in range(iterations):
gamma = Expectation(data, mu, sigma, alpha, K)
mu, sigma, alpha = Maximization(data, gamma, K)
#用最终的模型参数来计算所有样本对于各混合成分的后验概率,以此作为最终簇划分的依据
gamma = Expectation(data, mu, sigma, alpha, K)
print('mu',mu)
return gamma
附 求导过程

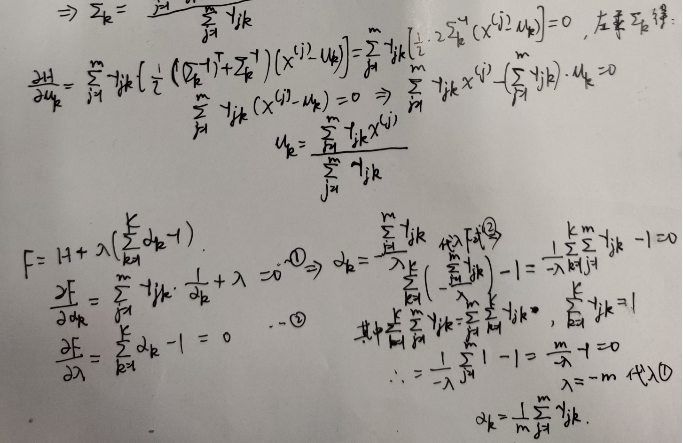
最后
以上就是粗暴云朵最近收集整理的关于GMM 模型与EM算法求解详细推导1. 高斯模型与高维高斯模型介绍2. 高斯混合模型3. EM算法来估计高斯混合模型的参数 4 代码附 求导过程 的全部内容,更多相关GMM内容请搜索靠谱客的其他文章。








发表评论 取消回复