1,先修知识
微积分,线性代数,概率论

参考教材,其中第一本的中译版非常值得一读.
2,课程的五大理念,也可以说是整个学习的五大理念.

建议读书时候将推算符号,抄下来.
另外清华大学张颢老师的随机过程导论部分,讲的非常好.可以看看顶尖的人是如何看这个世界的.
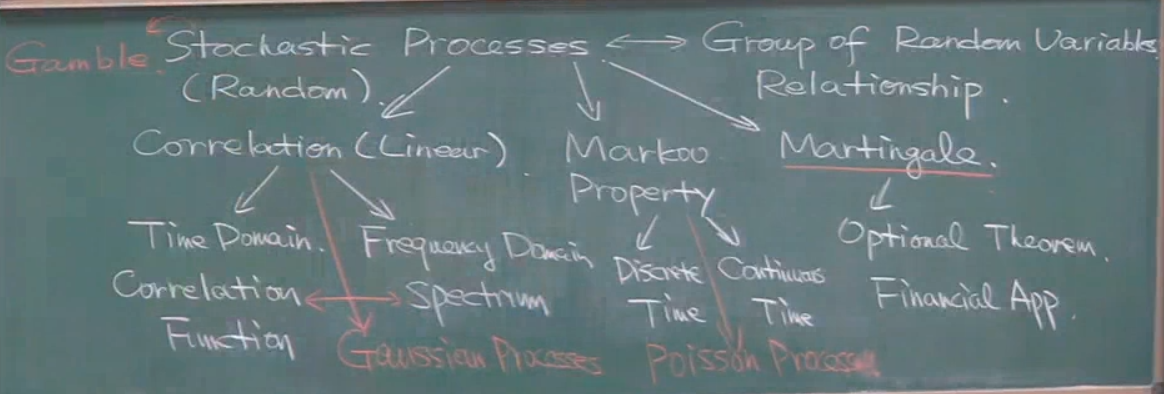
3,随机过程
stochastic processes 通俗来说就是一组随机变量之间的相互关系.
目前认知的三种相互关系:
(1),相关,线性
主要分为时域上(相关函数)
频域上为功率谱密度
并且相关函数与功率谱密度存在密切联系.
典型的线性随机过程:高斯随机过程
(2),马尔可夫过程
马尔可夫链也可以分为连续过程与离散过程.
马尔可夫性非常符合人类习惯所以应用广泛.
马尔可夫性就是你未来的状态仅仅取决于现在,而与过去没有关系.
典型的马尔可夫过程就是泊松过程.
(3),martingale过程(鞅过程)
4,

所以F为联合分布函数,f为联合概率密度函数

通俗理解分布函数

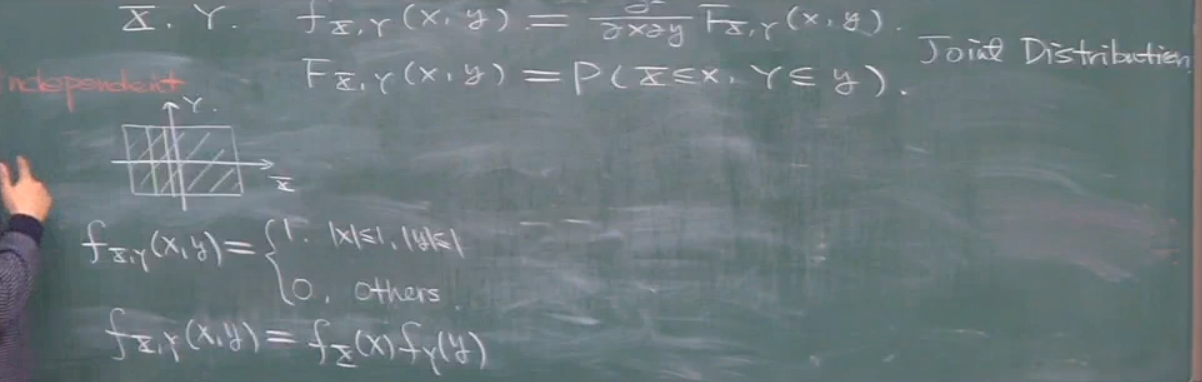
对于上图有两个注意的点,
第一个就是分布函数与密度函数.并且概率密度函数的在一个区间内的积分就是函数落在这个区间内的概率.

对于分布函数来说,某一个区间内的概率为F(b)-F(a)=P(a<x<=b)
第二个就是如上图的均匀分布的概率密度函数为面积的倒数,所以说,图片中的概率密度可能是错的,应该是1/4.并且对于x,y独立,其联合密度函数可以写成两个边缘密度函数相乘.
如何看出x,y独立,因为在图中,随着x的变化,y的分布都是从-1到1是不变的,所以独立.
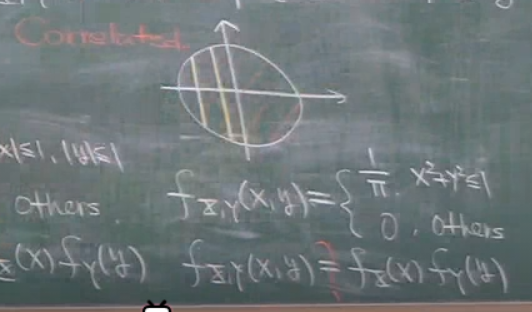
在这个例子中,概率密度函数依然是面积的倒数,但是x,y相关联了.
为什么?因为x变化可以造成y分布的变化,在图上变现为两条直线不同.
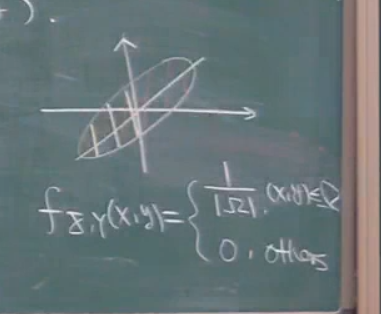
第三个例子,x,y依然是相关的,并且随着x的增大,y的分布也在一定程度上增大.(y的每个取值的均值在增大),所以就可以说是,x,y有线性关系.但是,可以看到y的分布是有宽度的,所以x,y的线性关系并不严格,这样就产生了
相关系数来描述这一相关性.通俗来说,相关系数描述的就是这个纺锤的胖瘦.
如果相关系数越大,就说明x,y越相关,纺锤越瘦.
极端情况下就是一条线,严格的线性关系.
这样我们就在两个随机变量之间,定义出了线性关系.如何理解呢?
原来的线性是对应一个具体的值,但是在随机变量中,对应一个范围,另一个变量在其中随机选取值.
注意均值与数学期望是没有关系的,他们只有通过大数定理产生关联.
另外,方差可以用期望来表示
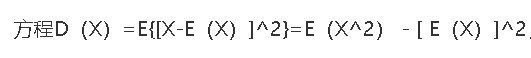
顺着思路,y与x成线性
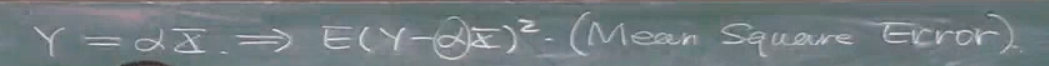
注意后面的E的式子就是y随机变量的方差,也就是我们常用到的均方误差.这里也就可以看出来,αx就是y的期望.上面说的y的均值,也是广义上的均值,再者说连续函数如何求均值?,所以其实就表示期望.
其中α反应的是直线的斜率,并且方差也就表示了纺锤的胖瘦.
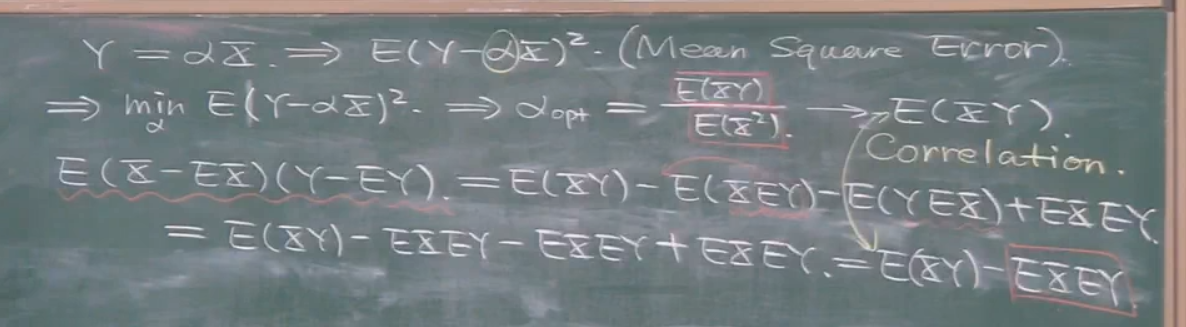
以上是最熟悉的调优过程,并且从概率的角度,得到了最优参数的公式.其中
E(XY)就可以说是反映了x,y的相关性.相关函数还有另一种表示,经过推导发现两个结果,只相差一个常数项,也可以说是,第二个结果进行了中心化.其中E(XEY)中的EY为什么可以提出去?因为EY就是一个常数,期望E进行的是随机变量的操作,而EY没有随机性.
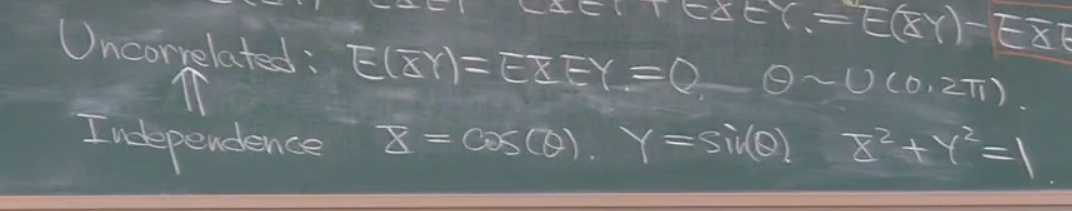
不相关就表示E(XY)=0,用第二个定义就等于一个常数,并且一般假定均值为0,所以一般也等于0.
注意独立不等于不相关,独立的条件更强.
如例子:对于(0,2pi)上的均匀分布,显然sin与cos不独立,因为存在关系是一个圆.
下面来计算x,y是否相关
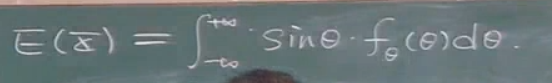
有x的期望等于x乘以参数的概率密度函数在无穷上的积分.
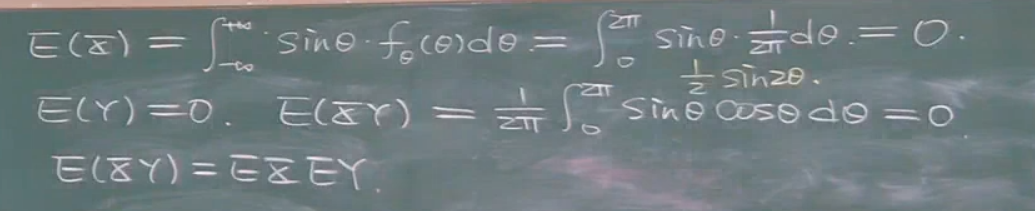
得到x,y不相关,但是不独立.x,y有关联,但是关联没有体现在相关这一层面上.
所以说,相关性描述随机变量关系的时候有局限性.并不能得到独立.
有相关,一定不独立.独立一定不相关.
从几何上理解相关
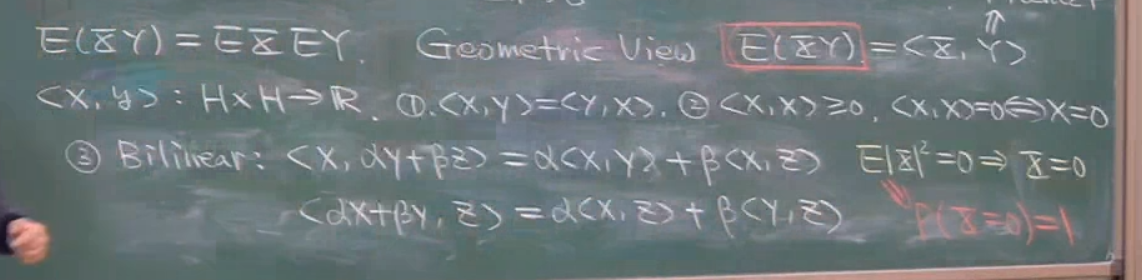
E(XY)在一定程度上可以理解为线性代数中的内积.
这里我们只要证明E(XY)满足内积的三条性质即可,其中第二条有些许偏差.这里注意是x平方的期望.这就可以推出x=0的概率为1.
这样我们把相关看成了内积.
而内积拥有几何含义,代表两个向量之间的角度.算式如下:
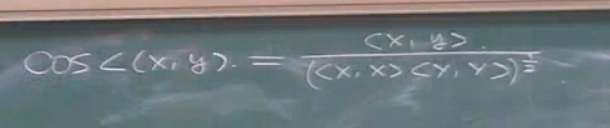
并且x,y的内积就是相关系数.
这样就从几何角度上描述相关,并且可以把随机变量x,y看成是矢量.所以对于相关性,对于两个随机变量我们可以算夹角.式子如下:
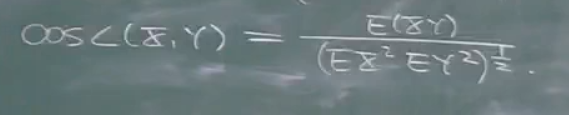
夹角的余弦就是相关系数.
那么如何保证上面等式的结果在-1到1之间呢?
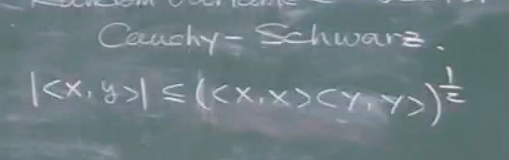
用柯西需瓦茨不等式即可证明.
证明该不等式非常容易
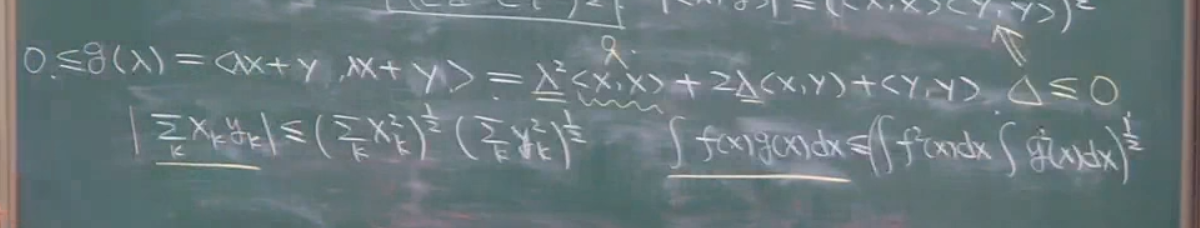
如上,定义一个g(λ)函数的内积,那么内积一定>=0,将式子展开得λ的一个二次函数,并且开口向上,所以函数一定只有1个或0个根,那么判别式一定<=0,这样讲判别式写成就得以证明.
下面是柯西需瓦茨不等式的其他形式,区别就是内积定义的不同,可能内积的点多就成了积分,离散的点就成了第一种形式.

这样我们从向量角度再次看寻找最优参数,就是在x方向上找一点,使得y与x的距离最短.
并且根据长度×方向写出了参数α,经过化简(注意其中穿插了期望与模长的转化,也就可以说(E(x的平方))再开方就表示x的模长),最后得到了与前面概率中相同的公式.(代数角度)
不禁想到线性代数中的解释,将b向量投影到a的列空间中(一条线),中间的线表示的就是误差,在垂直的时候误差最小.上面只是将垂直影藏于直角三角形中.
那么为什么都要取距离最小,就因为y-αx需要期望最小.看作矢量的话,期望就是中间线的模长.
所以之后,我们可以从几何角度得到结果,与代数角度得到的是相同的.
5,下面引入相关函数的概念
首先要了解随机过程,简单来说就是一堆随机变量.
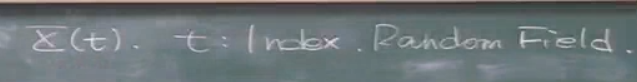
t表示随机变量的索引,一般为时间,如果t是二维的,那么随机过程就变成了随机场.
那么相关函数定义如下,
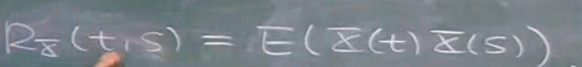
我们给定一个t就可以确定一组随机变量中的一个,那么x(t)与x(s)就对应于不同的随机变量,像前面的x,y.只不过现在可能表示两个时间点之间随机变量的相关性.这里的t,s可不代表二维变量.只是两个变量,称为自相关函数.反映同一函数在两个不同时间上的相关性.
相关研究的是两两之间的关系,我们就从两两开始,之后拓展到多个.
其中自相关函数有如下性质:
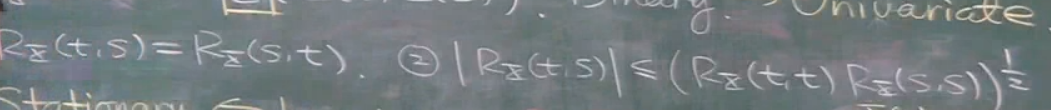
其实就是相关系数的性质.自相关函数是二元函数,那么如何将二元函数变为一元呢?就需要用到宽平稳的概念.
平稳性:指的是随机过程的某一类统计性质,随着时间的变化,不发生变化.
其中一种情况是宽平稳,它需要符合
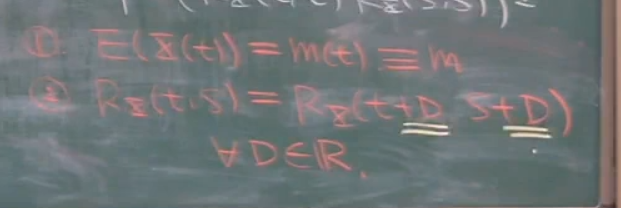
(1)随着时间的变化,随机过程的各个随机变量的均值保持不变,是一个常数
(2)其自相关函数,时间同时平移D,结果保持不变.
其中第二条更为重要,因为第一条我们用随机过程减去其均值,就可以符合第一条性质,而第二条不可以用一个确定性操作得到.
如果有第二条性质就说明,这个随机过程的相关函数只依赖于两个时刻的差值.因为同时加上任意时间D,都保持不变.对于宽平稳,也就可以将自相关函数写成如下式子.

下面是两个例子.
第一个例子,调制信号,A(t)为随机过程,cta参数是均匀分布,验证其宽平稳
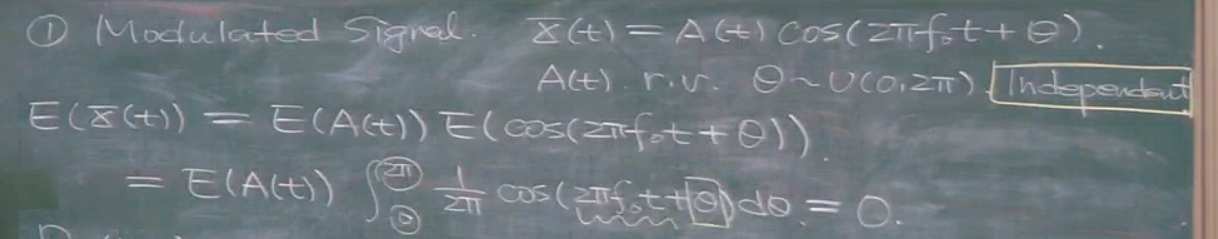
因为他们相互独立,所以他们的相关系数就等于他们期望的乘积,这里也许会有疑惑两部分都有t,怎么回独立,但是t是确定的,用确定的t来确定出两个随机变量,所以是独立的.
根据定义可以得到两个的期望表达式,第二个就是f乘以概率密度函数的积分,其中这个积分,由于是对cta积分,所以前面的一堆都是初始相位,2pi一定为其周期.积分值为0.

以上是对自相关函数的证明,这里需要补充条件,就是A(t)随机过程是宽平稳过程.第二项=0的理由和之前一样,都是在一个周期中积分.
这里也可以看到A(t)就是振幅调制.表示将调制信号放在振幅中传输
例二,随机电报信号

这个信号只有两个值1和-1,并且在时间段[s,t]之间,翻转次数k符合泊松分布.
那么求E(x(t)x(s))就用最原始的定义,值乘以其概率.P1为翻转偶数次,-1为翻转奇数次.
然后由于k从0加到无穷,P为1所以可以得到左下角的等式,这样我们将其中λ替换为-λ,就可以当k为奇数时,多项式为负,k为偶数时多项式为正.
这样当λ与-λ的两个式子相加时,得到了两倍的偶数项,奇次项相互消掉.这样就得到了P1.
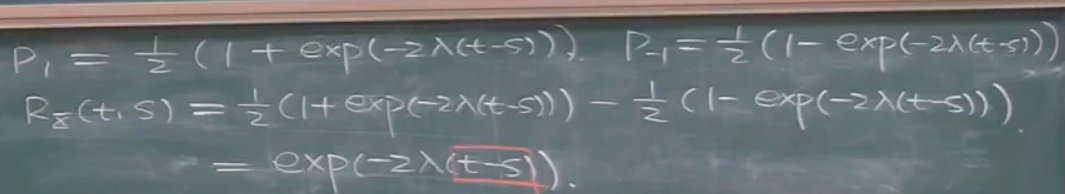
并求出自相关函数,只与时间间隔有关.这里随机电报信号的期望是个疑问.需要知道信号以多少概率取1以多少概率取-1,注意求期望的时候,t是确定的.要求t随便取一个值,均值都不变.随机信号每一个时刻,都是按同样几率取值,所以说均值应该是不变的.因为各个时刻算法都相同.
由例一中cta求期望,可以看出,这个期望就是将一个随机变量的每个分布都乘以其对应的概率,对于连续函数就是积分.cta的分布在确定时间后就是0到2pi.相当于x,其他的就是初始相位.
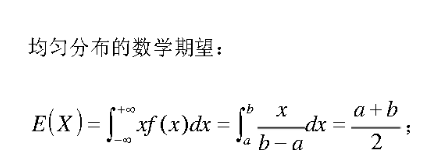
也要注意分布是没有自相关函数的,不可以说均匀分布的自相关函数.
最后
以上就是默默高跟鞋最近收集整理的关于随机过程基础1--随机过程与宽平稳的全部内容,更多相关随机过程基础1--随机过程与宽平稳内容请搜索靠谱客的其他文章。








发表评论 取消回复