概述
本次笔记从EM算法的求解目标出发，不仅进行了前提知识的介绍，而且后面还提供了保姆式的公式推导，并且在reference中给出了一系列优秀的blog，相信根据此文，再参考一点其他的blog，零基础也能够完全搞明白EM算法！
在学习EM算法之前，首先要明白以下几点内容：
①什么是隐变量？
例子一：
假设有一批样本属于三个类，每个类都服从正态分布，但是正态分布的均值、协方差等参数未知。
1，如果此时你知道这一批样本分别属于哪个类，那么就可以构造似然函数，然后求极值，求出参数。也就是最大似然估计。
2，你不知道这一批样本分别属于哪个类，那么此时无法直接使用最大似然估计，某个样本具体属于哪个类的这个变量，就是隐变量。
例子二：
比如一个学校有100人，男女各为50人。男生服从正态分布A，女生服从正态分布B。
那么就可以从这50个男生的身高中估计出
但是如果男女混在了一起，也就是只有100个身高数据，但是不知道具体是男生还是女生。
这个时候，就有点鸡生蛋还是蛋生鸡的感觉了，因为我们需要用知道精确的男女身高分布的参数，才能知道哪个样本是男是女的概率。但是我们只有知道的每个样本是男的还是女的，才能用最大似然估计精确的估计男女身高分布的参数。
这时候样本是男还是女的这个变量，也就是隐变量。
②什么是最大似然估计（存在即合理）？
可以参考下面马同学的文章，讲解的非常清晰易懂，关键就是要能够搞明白，概率和似然的区别、什么是似然函数。
马同学高等数学www.matongxue.com③jensen不等式：
若f(x)是凸函数，x是随机变量，则下面的不等式成立：
在这里E是数学期望，对于离散型随机变量，数学期望是求和，对连续型随机变量则为求定积分。如果f(x)是一个严格凸函数，当且仅当x是常数时不等式取等号：
EM算法推导：
EM算法的全称为：expectation maximization algorithm，分为两步，一步是expectation ，一步是maximization。
功能：用于求解含有隐变量（latent variable）的概率模型的参数的极大似然估计、或者极大后验估计。
用数学语言来说就是，假设我们有样本集{
对于求解参数估计
下面会对如下的公式进行详细的推导。
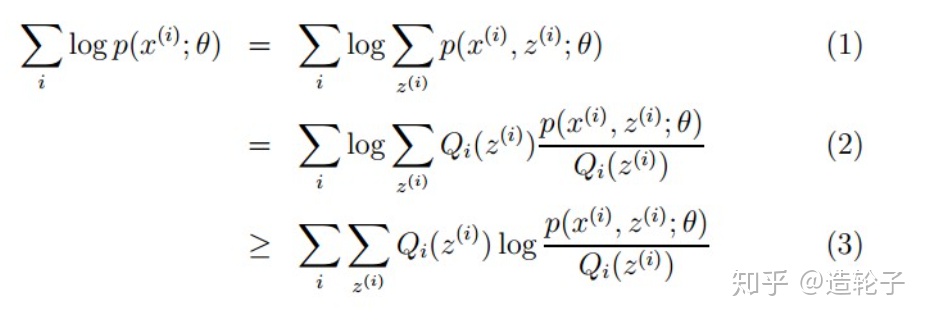
（1）中的两个式子，左边的式子代表的是似然函数，也就是我们最大化的目标，我们的目的就是为了求出似然函数的极值。右边的式子相当于在离散型变量的情形下，求出x变量的边缘概率密度。所以（1）中左右两个式子是等价的。
对于（2）和（3）来说，其实我们也可以直接对（1）进行求导求解，因为多了一个变量z，也就是多变量函数求极值而已。但是因为（1）中右边的式子是在log内求和的，求导之后函数形式过于复杂。所以这里为了解决这个求极值问题，运用jensen不等式，构造了（2）和（3）。
首先给出期望的公式（这里面的x，和上面推导中的x不同）。
在（2）中
所以
根据上面的jensen不等式，
由上面可以知道
因为最外层的
至此，上面的（1）（2）（3）公式均推导完毕！
不过到了这里有个问题，那就是咱们的目的是为了求极值啊，你这搞了半天，只是推导了一个下界而已，这有什么卵用？其实这就是“偷梁换柱”啦，因为原问题不好求解，所以求出他的一个下界来，求下界的极值，然后不断的逼近原问题的极值啦！
他的过程就像下图所示：
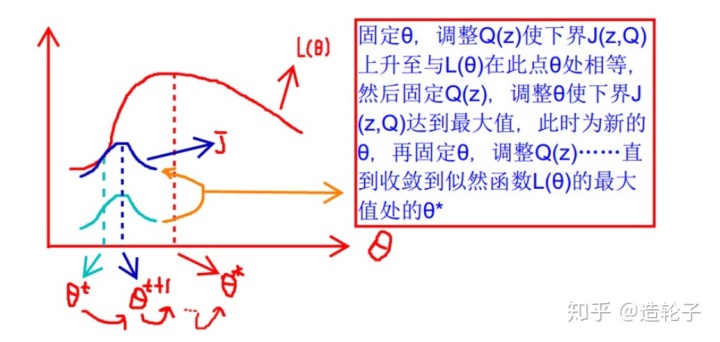
不过这里还可以再抛出来两个问题，首先①什么时候
②每次求解，为什么能保证
首先回答第一个问题，由上面的jensen不等式，我们可以知道如果f(x)是一个严格凸函数，当且仅当x是常数时不等式取等号：
所以
可以知道此时
因为c是和z等变量无关的，所以就可以假设：
也就是说，我们可以直接设定
由此①得证。
上面回答了第一个问题，其实就是解决了EM算法两个步骤中的E（expectation）步骤。
那么M步，就是在给定Q(z)的情况下，去计算最大似然估计，去不断的更新
那么这里就引出了第二个问题，每次求解，为什么能保证
我们假设
下面会分析下面的这个推导公式：
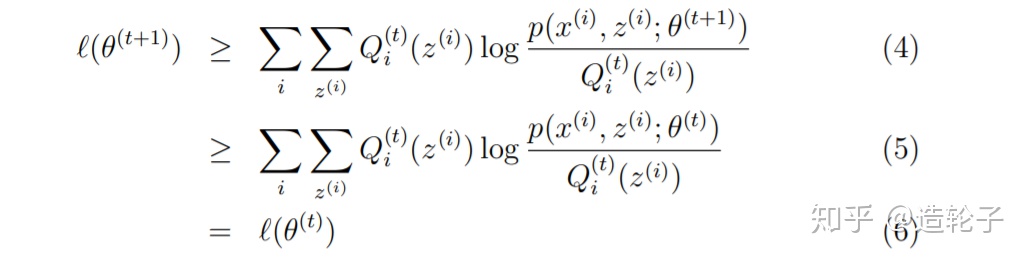
首先，我们在上面证明了如何取
也就是假设当前我们的
（4）式最好证明，因为根据前面的jensen不等式，对于任何的Q和
所以
接下来证明（5）：
（5）相当于运用了M步的定义，在M步就是为了将
就是求解如下公式：
所以（5）式肯定成立。
（6）式也显然是成立的。
至此，证明了②
证明了上面
当然也可以从坐标上升的角度去看待EM算法：
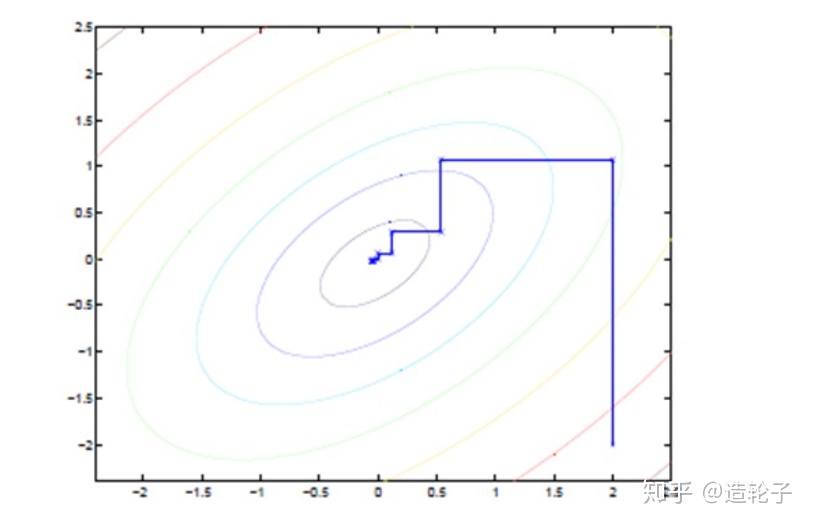
具体的讲述可以参考Andrew ng讲义里面的内容：
下面是更清晰一点的迭代图：
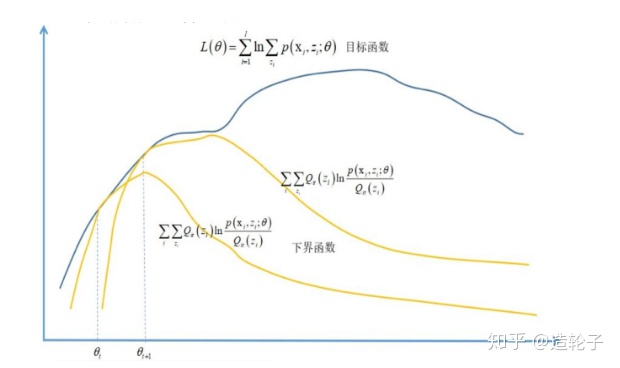
总结：
这次详细推导 了EM算法，但是应该只算是EM算法系列的第一步吧，用EM算法求解高斯混合模型、HMM、以及面试经常考的EM算法 和Kmeans的联系等内容，后续再写相关的系列文章。
参考：
理解EM算法www.tensorinfinity.com
最后
以上就是任性音响为你收集整理的em算法详细例子及推导_EM算法学习笔记（非常详细）的全部内容，希望文章能够帮你解决em算法详细例子及推导_EM算法学习笔记（非常详细）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复