随机过程（一）基础概念与随机过程基本类型

1.1 概率空间

• 随机试验
  

• 样本空间
  

• 事件
  
  $\Omega 中的元素e为样本点/基本事件。$
  $样本空间\Omega 称为必然事件，空集\varphi 称为不可能事件。$

• 事件运算
  

• 古典概率
  

• 几何概率
  

• 统计概率
  

• 概率的公理化定义
  

• 概率空间
  

• 条件概率
  

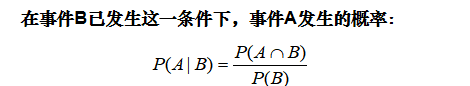
• 全概率
  

• 贝叶斯公式
  

• 独立事件
  

1.2 随机变量

• 定义
  
• 离散型随机变量

• 连续型随机变量
  
• 分布函数及其性质
  
• 离散分布列（律）
  
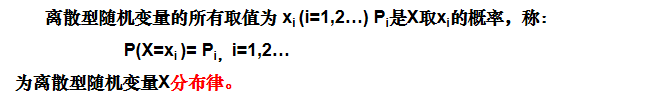
• 用分布列（律）描述离散型随机变量的概率分布
  
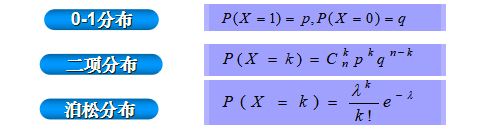
• 概率密度函数
  
• 用概率密度描述连续性随机变量的概率分布
  

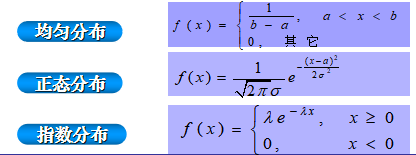
1.3随机变量函数的分布

• 定义及概率密度

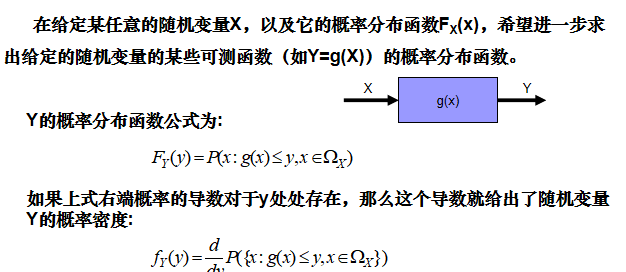
• 联合分布函数
  
• 边际分布
  
• 相互独立的随机变量
  
• 条件分布函数
  

1.4随机变量的数字特征

• 统计平均与数学期望
  
• 随机变量函数的数学期望值
  
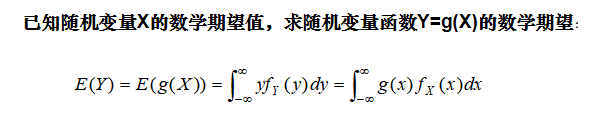
• 方差与协方差
  $K阶原点矩与K阶中心矩$
  
  
  协方差、相关系数
  
• 特征函数
  
• 独立与不相关
  
  
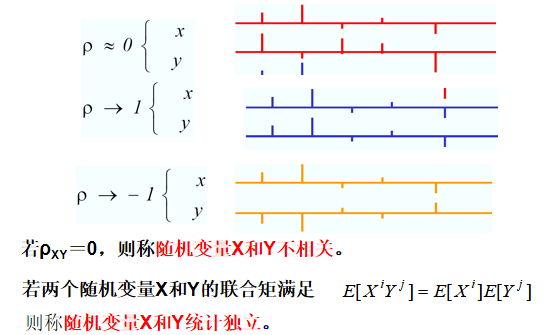
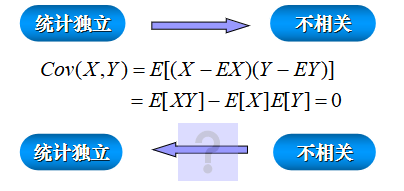
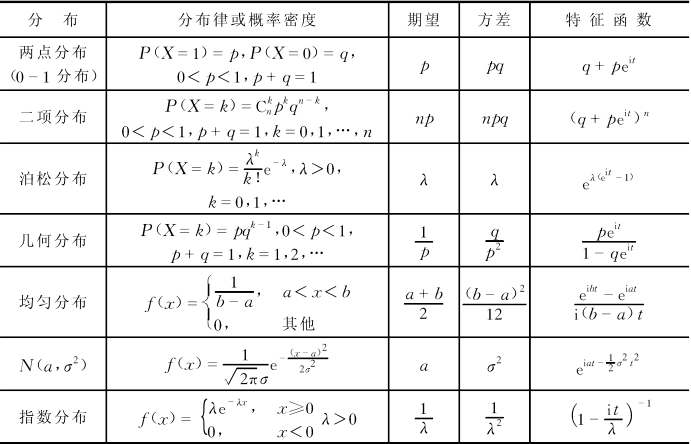
• 常见分布的期望、方差、特征函数

• 总结
  

1.5随机过程的定义和统计描述

自然界事物的变化过程分为两大类：

1. 具有确定形式的过程，可以用一个时间t的确定函数来描述。
2. 无确定的变化形式，不能用一个时间t的确定函数来描述。

• 随机过程
  我们必须对一些随机现象的变化过程进行研究,必须考虑无穷多个随机变量。针对这个问题，我们必须用一族随机变量才能刻画这种随机现象的全部统计规律。我们通常将随机变量族称为随机过程。

• 对于随机过程的理解
  
• 分类
  
  
  

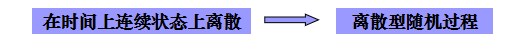
1.6 随机过程分布律和数字特征

• 随机过程的一维分布函数
  
• 随机过程的二维分布函数

• n维
  
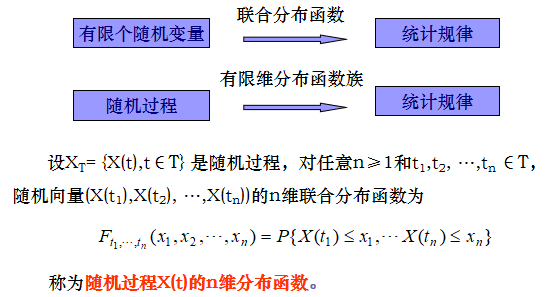
• 有限维分布函数族
  
• 有限维分布函数的性质：
  
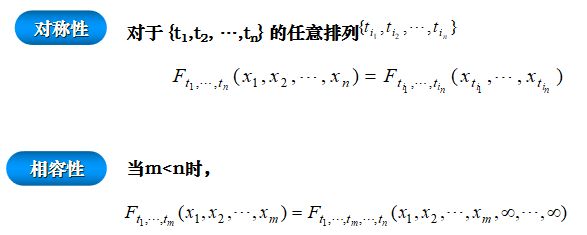
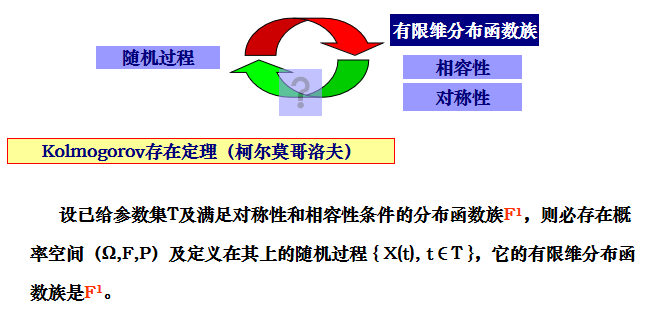
• 存在性
  
• 均值函数
  
• 均方值函数和方差函数
  
• 自相关函数
• 协方差函数
  
• 互协方差函数和互相关函数
  
• 相互独立、互不相关、相互正交
  

1.7 复随机过程

• 定义
  
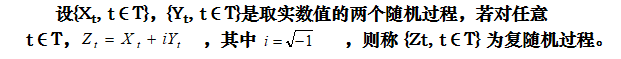
• 数字特征
  
• 复随机过程的互相关函数、互协方差函数
  

1.8 随机过程基本类型

最后

以上就是拼搏超短裙最近收集整理的关于随机过程（一）基础概念与随机过程基本类型的全部内容，更多相关随机过程（一）基础概念与随机过程基本类型内容请搜索靠谱客的其他文章。