1 梯度下降

数学解释：在微积分里面，对多元函数的参数求偏导，把求得的偏导数以向量的形式写出来，就是梯度。例如$f(x,y)$对$x,y$求偏导，求得的梯度向量就是${\left(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right)}^T$，多参数的梯度向量以此类推。从几何上讲，梯度向量所表示的含义是函数变化增加最快的地方，也就是沿着梯度的方向，更容易找到函数的最大值，反之，沿着梯度向量的反方向，更容易找到函数的最小值。

直观解释：寻找函数最小值的过程好比下山的过程，假设我们身处大山的某个位置，不知道怎么下山，这个时候我们就会走一步算一步。走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的方向向下走一步，然后继续算梯度，直到已经下不去了。这种做法存在的一个问题是也许我们到不了真正的山脚，而是到了某一个局部的山峰低处，也就是我们所说的局部最优解。

1.1 批量梯度下降法（BGD: Batch Gradient Descent）

迭代规则：每次迭代采用整个训练集数据来计算损失函数$J\left(\theta \right)$对于参数$\theta$的梯度（计算数据集上每个样本的损失之和，再对参数求偏导，进行梯度下降）。这里的batch指的就是整个数据集。每次迭代的参数更新参数如下：

优点：每一步迭代使用了全部样本，因此损失函数收敛过程比较稳定。对于凸函数可以收敛到全局最优值，对于非凸函数可以收敛到局部最小值。

缺点：每一步更新都要利用全部样本计算梯度，计算起来比较慢，遇到大量数据时比较棘手，而且不能投入新的数据实时更新模型。

1.2 随机梯度下降法（SGD: Stochastic Gradient Descent）

迭代规则：每一步迭代使用一个样本计算损失函数对$\theta$的梯度。公式如下：

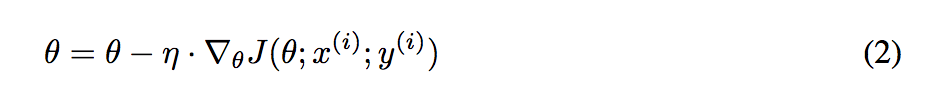
优点：每次计算一个样本，训练速度快包含一定的随机性，从期望来看，每次计算的梯度基本都是正确的导数。

缺点：更新频繁，带有随机性，会导致损失函数收敛的过程中严重震荡。

1.3 小批量梯度下降法（MBGD：Mini-Batch Gradient Descent）

迭代规则：BGD和SGD的折中，在数据集中取一小批样本计算梯度。迭代公式如下：

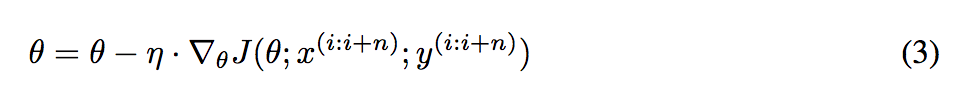
优点：降低参数更新时的方差，收敛更加稳定，另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。

缺点：不能保证很好的收敛性，learning rate 如果选择的太小，收敛速度会很慢，如果太大，损失函数就会在极小值处不停地震荡甚至偏离。（有一种措施是先设定大一点的学习率，当两次迭代之间的变化低于某个阈值后，就减小 learning rate，不过这个阈值的设定需要提前写好，这样的话就不能够适应数据集的特点。）

梯度下降的三种算法都可能会陷入鞍点和平摊底部。

2 Momentum

梯度下降存在的两个问题：

1.容易陷入局部最优，而无法达到全局最优；
2. 有时候梯度下降法的收敛速度还是很慢。

为了解决以上两个问题，提出了动量法。计算公式如下：

引入了动量项，将历史梯度进行累加，使得在梯度相同的方向上，更新速度变快，而在梯度不同的方向上，更新速度变慢，这样可以加速收敛，减小震荡。

优点：前后梯度一致时加快收敛；前后梯度不一致时能够抑制震荡，越过局部最优。（加快收敛，减少震荡）

缺点：引入了一个超参数。（一般取0.9左右）

3 Adagrad：Adaptive gradient algorithm

Adagrad算法设置一个全局学习率$\epsilon$，为了保证分母不为0，设置一个小常数$\delta$，$\odot$表示对应元素相乘，将梯度$g$的对应元素相乘累加到变量$r$上，这种按元素运算的方法使得目标函数自变量中的每个元素都分别有了自己的学习率。

优点：学习率自适应而不用手动调节。

缺点：分母不断累积，学习率不断变小，如果学习率在迭代早期降得较快且当前解依然不佳的话，AdaGrad算法在迭代后期由于学习率过小。可能较难找到一个有用的解。

4 RMSProp

为了解决Adagrad算法中存在的问题，即学习率在早期下降较快，如果在前期没有找到一个合适的解的话，后期学习率太低也不容易找到一个好的解。为此提出了RMSProp，在Adagrad算法的基础上做了一些改动。

引入一个衰减系数，让$r$每次以一定的比例衰减，衰减系数使用的是指数加权平均，消除了梯度下降中的抖动。

优点：相比于AdaGrad算法，这种方法解决了过早结束学习的问题，可直观地理解为迭代前期梯度的累加随着迭代次数的增加逐渐衰减，对往后迭代的梯度影响逐渐减少。

缺点：引入新的超参数衰减系数。

5 Adam: Adaptive Moment Estimation

Adam结合了动量法和RMSProp，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率，这里的一阶矩的估计即均值，二阶矩的估计和方差类似。然后对均值和方差进行矫正，由于二者的初始化为0，因此容易往0偏置，这样处理后会减少偏置的影响。Adam的优点主要在于经过偏置矫正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。
优点：Adam比其他适应性学习方法效果更好，更加适用于多种情况。这也是目前最常用的优化方法，适合于大多数模型的优化。
缺点：更加复杂，引入的超参数更多。

最后

以上就是酷炫路灯为你收集整理的深度学习之优化算法1 梯度下降2 Momentum3 Adagrad：Adaptive gradient algorithm4 RMSProp5 Adam: Adaptive Moment Estimation的全部内容，希望文章能够帮你解决深度学习之优化算法1 梯度下降2 Momentum3 Adagrad：Adaptive gradient algorithm4 RMSProp5 Adam: Adaptive Moment Estimation所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。