文章目录
- 第三章 多维随机变量及其分布
- 3.1二维随机变量及其分布函数
- 3.1.1 二维R.V.
- 3.1.2 二维离散型R.V.
- 3.1.3 二维连续型R.V.
- 3.2 边缘分布与R.V.独立性
- 3.2.1 边缘分布函数与R.V.独立性
- 3.2.2 离散型边缘分布
- 3.2.3 连续性边缘分布
- 3.3 条件分布与条件概率
- 3.3.1 离散型R.V.的条件分布
- 3.3.2 连续性R.V.的条件密度函数
- 3.4 二维随机变量函数的分布
第三章 多维随机变量及其分布
3.1二维随机变量及其分布函数
P ( ( X , Y ) ∈ G ) = { ∑ ( x i , y j ) ∈ G p i j , 离 散 型 ( 联 合 分 布 律 ) ∬ G ⋂ D f ( x , y ) d x d y , 连 续 型 ( 联 合 密 度 ) P((X,Y)in G)=begin{cases}begin{aligned}&sumlimits_{(x_i,y_j)in G}p_{ij},&离散型(联合分布律)\ &iintlimits_{Gbigcap D}f(x,y);dxdy,&连续型(联合密度) end{aligned}end{cases} P((X,Y)∈G)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧(xi,yj)∈G∑pij,G⋂D∬f(x,y)dxdy,离散型(联合分布律)连续型(联合密度)
3.1.1 二维R.V.
-
分布函数(联合分布函数):
-
定义: ( X , Y ) (X,Y) (X,Y) 为二维随机变量, ∀ ( x , y ) ∈ R 2 forall (x,y)in R^2 ∀(x,y)∈R2,称 F ( x , y ) = P { X ≤ x , Y ≤ y } color{red}F(x,y)=P{Xle x,Yle y } F(x,y)=P{X≤x,Y≤y} 为 ( X , Y ) (X,Y) (X,Y) 的分布函数。
-
解释:
F ( x , y ) = P ( X ≤ x , Y ≤ y ) ⏟ = P ( A ⋂ B ) = P ( A ) ⋅ P ( B ) ≠ P ( X ≤ x ) ⋅ P ( Y ≤ y ) ⏟ . 乘 积 的 概 率 乘 积 的 概 率 begin{aligned}F(x,y)=&underbrace{P(Xle x,Yle y)}=P(Abigcap B)=P(A)cdot P(B)ne &&underbrace{P(Xle x)cdot P(Yle y)}.\ &;;quad乘积的概率 &&;;qquad乘积的概率 end{aligned} F(x,y)= P(X≤x,Y≤y)=P(A⋂B)=P(A)⋅P(B)=乘积的概率 P(X≤x)⋅P(Y≤y).乘积的概率 -
矩形区域:
P { x 1 < X ≤ x 2 , y 1 < Y ≤ y 2 } = F ( x 2 , y 2 ) − F ( x 1 , y 2 ) − F ( x 2 , y 1 ) + F ( x 1 , y 1 ) . P{x_1< Xle x_2,y_1< Yle y_2 }=F(x_2,y_2)-F(x_1,y_2)-F(x_2,y_1)+F(x_1,y_1). P{x1<X≤x2,y1<Y≤y2}=F(x2,y2)−F(x1,y2)−F(x2,y1)+F(x1,y1). -
性质:
- 单调不减:当 x 1 < x 2 x_1<x_2 x1<x2,有 F ( x 1 , y ) ≤ F ( x 2 , y ) F(x_1,y)le F(x_2,y) F(x1,y)≤F(x2,y);当 y 1 < y 2 y_1<y_2 y1<y2,有 F ( x , y 1 ) ≤ F ( x , y 2 ) F(x,y_1)le F(x,y_2) F(x,y1)≤F(x,y2)
- 两侧端点: F ( − ∞ , − ∞ ) = F ( − ∞ , y ) = F ( x , ∞ ) = 0 , F ( + ∞ , − ∞ ) = 1 F(-infty,-infty)=F(-infty,y)=F(x,infty)=0,F(+infty,-infty)=1 F(−∞,−∞)=F(−∞,y)=F(x,∞)=0,F(+∞,−∞)=1
- 左右连续:对 ∀ x , y ∈ R forall x,yin R ∀x,y∈R,有 F ( x + 0 , y ) = F ( x , y + 0 ) = F ( x , y ) F(x+0,y)=F(x,y+0)=F(x,y) F(x+0,y)=F(x,y+0)=F(x,y)
- 非负性:对 ∀ x 1 < x 2 , y 1 < y 2 ∈ R forall x_1<x_2,y_1<y_2in R ∀x1<x2,y1<y2∈R,有 F ( x 2 , y 2 ) − F ( x 1 , y 2 ) − F ( x 2 , y 1 ) + F ( x 1 , y 1 ) ≥ 0 F(x_2,y_2)-F(x_1,y_2)-F(x_2,y_1)+F(x_1,y_1)ge 0 F(x2,y2)−F(x1,y2)−F(x2,y1)+F(x1,y1)≥0
-
3.1.2 二维离散型R.V.
离散型:取有限个或可数无穷个点对 ( x i , y i ) (x_i,y_i) (xi,yi)
-
分布律(联合分布律):
- 定义: P ( X = x i , Y = y i ) = p i j , i , j = 1 , 2 , . . . color{red}P(X=x_i,Y=y_i)=p_{ij},qquad i,j=1,2,... P(X=xi,Y=yi)=pij,i,j=1,2,...
- 性质:
- p i j ≤ 0 , i , j = 1 , 2 , . . . p_{ij}le 0,qquad i,j=1,2,... pij≤0,i,j=1,2,...
- ∑ i , j p i j = 1 sumlimits_{i,j}p_{ij}=1 i,j∑pij=1
-
二维分布函数: F ( x , y ) = ∑ x i ≤ x ∑ y i ≤ y p i j F(x,y)=sumlimits_{x_ile x}sumlimits_{y_ile y}p_{ij} F(x,y)=xi≤x∑yi≤y∑pij
3.1.3 二维连续型R.V.
-
密度(联合密度):
-
定义:
F ( x , y ) = ∫ − ∞ x ∫ − ∞ y f ( u , v ) d u d v f ( x , y ) = ∂ 2 F ( x , y ) ∂ x ∂ y color{red}F(x,y)=int_{-infty}^xint_{-infty}^yf(u,v);dudv\ color{red}f(x,y)=dfrac{partial^2 F(x,y)}{partial xpartial y} F(x,y)=∫−∞x∫−∞yf(u,v)dudvf(x,y)=∂x∂y∂2F(x,y)
密度函数 f ( x , y ) > 0 f(x,y)>0 f(x,y)>0 的区域为连续性 R . V . ( X , Y ) R.V.(X,Y) R.V.(X,Y) 的取值区域 -
性质:
- f ( x , y ) ≥ 0 , ( x , y ) ∈ R 2 f(x,y)ge 0,(x,y)in R^2 f(x,y)≥0,(x,y)∈R2
- ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d x d y = 1 int_{-infty}^{+infty}int_{-infty}^{+infty}f(x,y);dxdy=1 ∫−∞+∞∫−∞+∞f(x,y)dxdy=1
-
-
知识点:已知联合密度 f ( x , y ) f(x,y) f(x,y) 求概率 P ( ( X , Y ) ∈ G ) P((X,Y)in G) P((X,Y)∈G) —— 本质是曲顶柱体体积 V = ∬ D ⋂ G f ( x , y ) d x d y V=iintlimits_{Dbigcap G} f(x,y);dxdy V=D⋂G∬f(x,y)dxdy
- ⨀ color{red}bigodot ⨀ 1. 先画 D D D,再画 G G G
- ⨀ color{red}bigodot ⨀ 2. 画箭头,选择 x / y x/y x/y 积分方向
- ⨀ color{red}bigodot ⨀ 3. 解释积分上下限
例题 color{White}colorbox{Fuchsia}{例题} 例题:有密度函数 f ( x , y ) = { A y , 0 < y < x < 1 0 , o t h e r s f(x,y)=begin{cases}begin{aligned}&Ay,&0<y<x<1 \&0,&others end{aligned}end{cases} f(x,y)={Ay,0,0<y<x<1others
-
求 A A A
解:
1 = ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d x d y = ∫ 0 1 d x ∫ 0 x A y d y = A 6 ∴ A = 6 1=int_{-infty}^{+infty}int_{-infty}^{+infty} f(x,y);dxdy=int_0^1dxint_0^x Ay;dy=dfrac{A}{6}\ therefore A=6 1=∫−∞+∞∫−∞+∞f(x,y)dxdy=∫01dx∫0xAydy=6A∴A=6 -
求 P ( X ≤ 1 2 , Y ≤ 1 4 ) P(Xle dfrac{1}{2},Yle dfrac{1}{4}) P(X≤21,Y≤41)
解:
P ( X ≤ 1 2 , Y ≤ 1 4 ) = ∫ − ∞ 1 2 d x ∫ − ∞ 1 4 f ( x , y ) d y = ∫ 0 1 4 d y ∫ y 1 2 6 y d y = 1 16 P(Xle dfrac{1}{2},Yle dfrac{1}{4})=int_{-infty}^{1over 2}dxint_{-infty}^{1over 4} f(x,y);dy=int_0^{1over 4}dyint_y^{1over 2} 6y;dy=dfrac{1}{16} P(X≤21,Y≤41)=∫−∞21dx∫−∞41f(x,y)dy=∫041dy∫y216ydy=161 -
求 P ( X + Y ≤ 1 2 ) , P ( X + Y ≤ 3 2 ) P(X+Yle dfrac{1}{2}),P(X+Yle dfrac{3}{2}) P(X+Y≤21),P(X+Y≤23)
解:
P ( X + Y ≤ 1 2 ) = ∫ 0 1 4 d y ∫ y 1 2 − y 6 y d x = ∫ 0 1 4 6 y ( 1 2 − 2 y ) d y = 1 32 注意对x积分时内部是对y的函数 P ( X + Y ≤ 3 2 ) = ∫ 0 3 4 d x ∫ 0 x 6 y d y + ∫ 3 4 1 d x ∫ 0 3 2 − x 6 y d y = 23 32 begin{aligned}&P(X+Yle dfrac{1}{2})=int_0^{1over 4}dyint_y^{{1over 2}-y} 6y;dx= int_0^{1over 4}6y({1over 2}-2y);dy =dfrac{1}{32} color{red}text{ 注意对x积分时内部是对y的函数}\ &P(X+Yle dfrac{3}{2})= int_0^{3over 4}dxint_0^x 6y;dy+int_{3over 4}^1dxint_0^{{3over 2}-x}6y;dy=dfrac{23}{32} end{aligned} P(X+Y≤21)=∫041dy∫y21−y6ydx=∫0416y(21−2y)dy=321 注意对x积分时内部是对y的函数P(X+Y≤23)=∫043dx∫0x6ydy+∫431dx∫023−x6ydy=3223

-
二维均匀分布:
- 解释:等可能的落入区域 G G G 的随机点。
- 定义: f ( x , y ) = { 1 S ( G ) , ( x , y ) ∈ G 0 , o t h e r s . f(x,y)=begin{cases}begin{aligned}&dfrac{1}{S(G)},&(x,y)in G\&0,&others. end{aligned}end{cases} f(x,y)=⎩⎪⎨⎪⎧S(G)1,0,(x,y)∈Gothers.,其中 S ( G ) S(G) S(G) 为 G G G 的面积
- 表示: ( X , Y ) ∼ U ( G ) (X,Y)sim U(G) (X,Y)∼U(G)
- 结论:若 ( X , Y ) ∼ U ( G ) (X,Y)sim U(G) (X,Y)∼U(G),则 P ( ( X , Y ) ∈ G ) = S D ⋂ G S D P((X,Y)in G)=dfrac{S_{Dbigcap G}}{S_D} P((X,Y)∈G)=SDSD⋂G
3.2 边缘分布与R.V.独立性
3.2.1 边缘分布函数与R.V.独立性
-
边缘分布函数:
F X ( x ) ≐ F ( x , + ∞ ) = P { X ≤ x , Y ≤ + ∞ } = F ( x , + ∞ ) F Y ( y ) ≐ F ( + ∞ , y ) = P { X ≤ + ∞ , Y ≤ y } = F ( + ∞ , y ) color{red}F_X(x)doteq F(x,+infty)=P{Xle x,Yle +infty }=F(x,+infty)\ color{red}F_Y(y)doteq F(+infty,y)=P{Xle +infty,Yle y}=F(+infty,y) FX(x)≐F(x,+∞)=P{X≤x,Y≤+∞}=F(x,+∞)FY(y)≐F(+∞,y)=P{X≤+∞,Y≤y}=F(+∞,y) -
独立性:
- 定义:对 ∀ x , y forall x,y ∀x,y,有 F ( x , y ) = F X ( x ) F Y ( y ) color{red}F(x,y)=F_X(x)F_Y(y) F(x,y)=FX(x)FY(y),则称 X X X 与 Y Y Y 相互独立。此时通过边缘分布可得到二位分布函数。
- 定理:设随机变量 X , Y X,Y X,Y 相互独立,且 g ( x ) , h ( y ) g(x),h(y) g(x),h(y) 分别是 x , y x,y x,y 的连续函数,则 X 1 = g ( X ) X_1=g(X) X1=g(X) 与 Y 1 = h ( Y ) Y_1=h(Y) Y1=h(Y) 也相互独立。
- 注意:
- 交事件的概率: F ( x , y ) = P ( X ≤ x , Y ≤ y ) F(x,y)=P(Xle x,Yle y) F(x,y)=P(X≤x,Y≤y)
- 概率的乘积: F X ( x ) ⋅ F Y ( y ) = P ( X ≤ x ) ⋅ P ( Y ≤ y ) F_X(x)cdot F_Y(y)=P(Xle x)cdot P(Yle y) FX(x)⋅FY(y)=P(X≤x)⋅P(Y≤y)
3.2.2 离散型边缘分布
-
边缘概率分布(边缘分布):
-
定义:
p i ⋅ = P ( X = x i ) = ∑ j p i j , i = 1 , 2 , . . . p ⋅ j = P ( Y = y j ) = ∑ i p i j , j = 1 , 2 , . . . color{red}p_{icdot}=P(X=x_i)=sumlimits_{j}p_{ij},qquad i=1,2,...\ color{red}p_{cdot j}=P(Y=y_j)=sumlimits_{i}p_{ij},qquad j=1,2,...\ pi⋅=P(X=xi)=j∑pij,i=1,2,...p⋅j=P(Y=yj)=i∑pij,j=1,2,... -
定理: X X X 与 Y Y Y 独立 ⟺ p i j = p i ⋅ ⋅ p ⋅ j {color{red}iff} p_{ij}=p_{icdot}cdot p_{cdot j} ⟺pij=pi⋅⋅p⋅j
例题 color{White}colorbox{Fuchsia}{例题} 例题:二维概率分布 ( X , Y ) (X,Y) (X,Y) 如图,若事件 ( X = 1 ) (X=1) (X=1) 与 ( X + Y = 1 ) (X+Y=1) (X+Y=1) 相互独立,求 a , b a,b a,b 并判断 X , Y X,Y X,Y 之间的独立性。
-

解:
P
(
X
=
1
)
P
(
X
+
Y
=
1
)
=
P
(
X
=
1
,
X
+
Y
=
1
)
=
P
(
X
=
1
,
Y
=
0
)
即
(
b
+
0.1
)
(
a
+
b
)
=
0.1
∵
a
+
b
=
0.5
∴
a
=
0.4
,
b
=
0.1
也
发
现
X
,
Y
独
立
P(X=1)P(X+Y=1)=P(X=1,X+Y=1)=P(X=1,Y=0)\ 即(b+0.1)(a+b)=0.1\ because a+b=0.5therefore a=0.4,b=0.1\ 也发现X,Y独立
P(X=1)P(X+Y=1)=P(X=1,X+Y=1)=P(X=1,Y=0)即(b+0.1)(a+b)=0.1∵a+b=0.5∴a=0.4,b=0.1也发现X,Y独立
3.2.3 连续性边缘分布
-
边缘密度函数:
-
定义:
f X ( x ) = ∫ − ∞ + ∞ f ( x , y ) d y , − ∞ < x < + ∞ f Y ( y ) = ∫ − ∞ + ∞ f ( x , y ) d x , − ∞ < y < + ∞ color{red}f_X(x)=int_{-infty}^{+infty} f(x,y)dy,qquad -infty<x<+infty\ color{red}f_Y(y)=int_{-infty}^{+infty} f(x,y)dx,qquad -infty<y<+infty\ fX(x)=∫−∞+∞f(x,y)dy,−∞<x<+∞fY(y)=∫−∞+∞f(x,y)dx,−∞<y<+∞ -
定理: X X X 与 Y Y Y 独立 ⟺ f ( x , y ) = f X ( x ) f Y ( y ) {color{red}iff} f(x,y)=f_X(x)f_Y(y) ⟺f(x,y)=fX(x)fY(y) 在三个密度函数的公共连续点处成立。
-
-
知识点:已知联合密度 f ( x , y ) f(x,y) f(x,y) 求边缘密度
- ⨀ color{red}bigodot ⨀ 1. 画图,画 D D D
- ⨀ color{red}bigodot ⨀ 2. 对二元函数的一元积分
- ⨀ color{red}bigodot ⨀ 3. 判断定义域
f ( x , y ) { ⟶ 对 y 积 分 f X ( x ) = { ∫ c ( x ) d ( x ) f ( x , y ) d y , x ∈ [ a , b ] 0 , o t h e r s ⟶ 对 x 积 分 f Y ( y ) = { ∫ a ( y ) b ( y ) f ( x , y ) d x , y ∈ [ c , d ] 0 , o t h e r s f(x,y)begin{cases}begin{aligned}&overset{对y积分}{longrightarrow}f_X(x)=begin{cases}&int_{c(x)}^{d(x)}f(x,y);dy,&color{red}xin[a,b]\&0,&others end{cases} \&overset{对x积分}{longrightarrow}f_Y(y)=begin{cases}&int_{a(y)}^{b(y)}f(x,y);dx,&color{red}yin[c,d]\&0,&othersend{cases} end{aligned}end{cases} f(x,y)⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧⟶对y积分fX(x)={∫c(x)d(x)f(x,y)dy,0,x∈[a,b]others⟶对x积分fY(y)={∫a(y)b(y)f(x,y)dx,0,y∈[c,d]others
3.3 条件分布与条件概率
-
条件分布函数: F X ∣ Y ( x ∣ y ) = P ( X ≤ x ∣ Y = y ) , x ∈ R {color{red}F_{X|Y}(x|y)=P(Xle x|Y=y)},qquad xin R FX∣Y(x∣y)=P(X≤x∣Y=y),x∈R 为 Y = y Y=y Y=y 条件下 X X X 的条件分布函数
当 X , Y X,Y X,Y 不独立时,条件分布函数是研究 X X X 与 Y Y Y 间相互关系的工具
3.3.1 离散型R.V.的条件分布
-
条件分布律:
- 定义:对于固定的 j j j,有 p ⋅ j > 0 p_{cdot j}>0 p⋅j>0,称 P ( X = x i ∣ Y = y i ) = p i j p ⋅ j {color{red}P(X=x_i|Y=y_i)=dfrac{p_{ij}}{p_{cdot j}}} P(X=xi∣Y=yi)=p⋅jpij 为 Y = y j Y=y_j Y=yj 的条件下 X X X 的条件分布律。 Y Y Y 的条件分布律同理。
- 性质:
- P ( X = x i ∣ Y = y i ) ≥ 0 , i = 1 , 2 , . . P(X=x_i|Y=y_i)ge 0,quad i = 1,2,.. P(X=xi∣Y=yi)≥0,i=1,2,..
- ∑ i P ( X = x i ∣ Y = y i ) = ∑ i p i j p ⋅ j = 1 sumlimits_{i} P(X=x_i|Y=y_i)=sumlimits_{i}dfrac{p_{ij}}{p_{cdot j}}=1 i∑P(X=xi∣Y=yi)=i∑p⋅jpij=1
-
三律关系:
联合分布律 边缘分布律 条件分布律 P ( X = x i , Y = y j ) = p i j P(X=x_i,Y=y_j)=p_{ij} P(X=xi,Y=yj)=pij P ( X = x i ) = ∑ j = 1 ∞ p i j = p i ⋅ P(X=x_i)=sumlimits_{j=1}^infty p_{ij}=p_{icdot} P(X=xi)=j=1∑∞pij=pi⋅ $P(Y=y_j P ( A i B j ) P(A_iB_j) P(AiBj) P ( A i ) P(A_i) P(Ai) 已知 X = x i X=x_i X=xi 时,$P(B_j -
已知联合分布律,可得到边缘分布律,进而得到条件分布律
-
通过边缘分布律和条件分布律可逆推出联合分布律
例题 color{White}colorbox{Fuchsia}{例题} 例题:从1,2,3中任意取一个数 X X X,在从1到 X X X 中任意取一个数 Y Y Y,求 Y Y Y 的分布律
解:
已 知 P ( X = x i ) = 1 3 , P ( Y = j ∣ X = i ) = 1 i 则 联 合 分 布 律 P ( X = i , Y = j ) = P ( X = i ) ⋅ P ( Y = j ∣ X = i ) = 1 3 i , ( i = 1 , 2 , 3 , j = 1 , 2 , i ) { P ( Y = 1 ) = 1 3 + 1 6 + 1 9 = 11 18 P ( Y = 2 ) = 1 6 + 1 9 = 5 18 P ( Y = 1 ) = 1 9 已知 P(X=x_i)=dfrac{1}{3},P(Y=j|X=i)=dfrac{1}{i}\ 则联合分布律P(X=i,Y=j)=P(X=i)cdot P(Y=j|X=i)=dfrac{1}{3i},qquad (i=1,2,3,j=1,2,i)\ begin{aligned}begin{cases}&P(Y=1)=dfrac{1}{3}+dfrac{1}{6}+dfrac{1}{9}=dfrac{11}{18} \ &P(Y=2)=dfrac{1}{6}+dfrac{1}{9}=dfrac{5}{18} \ &P(Y=1)=dfrac{1}{9}end{cases} end{aligned} 已知P(X=xi)=31,P(Y=j∣X=i)=i1则联合分布律P(X=i,Y=j)=P(X=i)⋅P(Y=j∣X=i)=3i1,(i=1,2,3,j=1,2,i)⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧P(Y=1)=31+61+91=1811P(Y=2)=61+91=185P(Y=1)=91
-
3.3.2 连续性R.V.的条件密度函数
-
条件分布函数:
-
定义:对任意 ϵ > 0 epsilon>0 ϵ>0,若极限 lim ϵ ⟶ 0 + P ( X ≤ x ∣ y − ϵ < Y ≤ y + ϵ ) limlimits_{epsilonlongrightarrow 0^+} P(Xle x|y-epsilon< Yle y+epsilon) ϵ⟶0+limP(X≤x∣y−ϵ<Y≤y+ϵ) 存在,则称此极限为条件 Y = y Y=y Y=y 下 X X X 的条件分布函数,记为
F X ∣ Y ( x ∣ y ) = P ( X ≤ x ∣ Y = y ) = lim ϵ ⟶ 0 + P ( X ≤ x ∣ y − ϵ < Y ≤ y + ϵ ) = lim ϵ ⟶ 0 + P ( X ≤ x , y − ϵ < Y ≤ y + ϵ ) P ( y − ϵ < Y ≤ y + ϵ ) color{red}F_{X|Y}(x|y)=P(Xle x|Y=y)=limlimits_{epsilonlongrightarrow 0^+} P(Xle x|y-epsilon< Yle y+epsilon)=limlimits_{epsilonlongrightarrow 0^+}dfrac{ P(Xle x,y-epsilon< Yle y+epsilon)}{P(y-epsilon< Yle y+epsilon)} FX∣Y(x∣y)=P(X≤x∣Y=y)=ϵ⟶0+limP(X≤x∣y−ϵ<Y≤y+ϵ)=ϵ⟶0+limP(y−ϵ<Y≤y+ϵ)P(X≤x,y−ϵ<Y≤y+ϵ) -
定理:二维随机变量 ( X , Y ) (X,Y) (X,Y) 有 f ( x , y ) f(x,y) f(x,y),则
F X ∣ Y ( x ∣ y ) = ∂ F ( x , y ) ∂ y F Y ′ ( y ) = ∫ − ∞ x f ( u , y ) f Y ( y ) d u , x ∈ R F Y ∣ X ( y ∣ x ) = ∂ F ( x , y ) ∂ x F X ′ ( x ) = ∫ − ∞ y f ( x , v ) f X ( x ) d v , y ∈ R F_{X|Y}(x|y)= dfrac{frac{partial F(x,y)}{partial y}}{F'_Y(y)} =int_{-infty}^x dfrac{f(u,y)}{f_Y(y)}du,quad xin R\ F_{Y|X}(y|x)= dfrac{frac{partial F(x,y)}{partial x}}{F'_X(x)} =int_{-infty}^y dfrac{f(x,v)}{f_X(x)}dv,quad yin R\ FX∣Y(x∣y)=FY′(y)∂y∂F(x,y)=∫−∞xfY(y)f(u,y)du,x∈RFY∣X(y∣x)=FX′(x)∂x∂F(x,y)=∫−∞yfX(x)f(x,v)dv,y∈R
-
-
条件密度:条件密度等于联合密度除以边缘密度
f X ∣ Y ( x ∣ y ) = ∂ F X ∣ Y ( x ∣ y ) ∂ x = f ( x , y ) f Y ( y ) f Y ∣ X ( y ∣ x ) = ∂ F Y ∣ X ( y ∣ x ) ∂ y = f ( x , y ) f X ( x ) color{red}f_{X|Y}(x|y)=dfrac{partial F_{X|Y}(x|y)}{partial x}=dfrac{f(x,y)}{f_Y(y)}\ color{red}f_{Y|X}(y|x)=dfrac{partial F_{Y|X}(y|x)}{partial y}=dfrac{f(x,y)}{f_X(x)}\ fX∣Y(x∣y)=∂x∂FX∣Y(x∣y)=fY(y)f(x,y)fY∣X(y∣x)=∂y∂FY∣X(y∣x)=fX(x)f(x,y) -
知识点:计算 Y = y Y=y Y=y 条件下 X X X 的概率
- ⨀ color{red}bigodot ⨀ 1. 已知 f ( x , y ) = { g ( x , y ) , ( x , y ) ∈ D 0 , o t h e r s f(x,y)=begin{cases}begin{aligned}&g(x,y),&&(x,y)in D\&0,&&others end{aligned}end{cases} f(x,y)={g(x,y),0,(x,y)∈Dothers
- ⨀ color{red}bigodot ⨀ 2. 则边缘密度 f X ( x ) = { ∫ c ( x ) d ( x ) f ( x , y ) d y , x ∈ [ a , b ] 0 , o t h e r s color{fuchsia}f_X(x)=begin{cases}begin{aligned}&int_{c(x)}^{d(x)}f(x,y)dy ,&&xin [a,b]\&0,&&others end{aligned}end{cases} fX(x)=⎩⎪⎨⎪⎧∫c(x)d(x)f(x,y)dy,0,x∈[a,b]others
- ⨀ color{red}bigodot ⨀ 3. 故得到当 y ∈ [ c , d ] yin[c,d] y∈[c,d] 时,条件密度 f X ∣ Y ( x ∣ y ) = { f ( x , y ) f Y ( y ) , x ∈ [ a ( y ) , b ( y ) ] 0 , o t h e r s color{green}f_{X|Y}(x|y)=begin{cases}begin{aligned}&dfrac{f(x,y)}{f_Y(y)} ,&&xin [a(y),b(y)]\&0,&&others end{aligned}end{cases} fX∣Y(x∣y)=⎩⎪⎨⎪⎧fY(y)f(x,y),0,x∈[a(y),b(y)]others
- ⨀ color{red}bigodot ⨀ 4. 求得概率 P ( X ∈ G ∣ Y = y 0 ) P(Xin G|Y=y_0) P(X∈G∣Y=y0),此时
X n e w ∼ f X ∣ Y ( x ∣ y ) = { f ( x , y 0 ) f Y ( y 0 ) , x ∈ [ a ( y 0 ) , b ( y 0 ) ] 0 , o t h e r s P ( X ∈ G ∣ Y = y 0 ) = ∫ G ⋂ D ( x ) f X ∣ Y ( x ∣ y 0 ) d x color{blue}X^{new}sim f_{X|Y}(x|y)=begin{cases}begin{aligned}&dfrac{f(x,y_0)}{f_Y(y_0)},&&color{red}xin [a(y_0),b(y_0)] \&0,&&others end{aligned}end{cases}\ P(Xin G|Y=y_0)=intlimits_{color{red}Gbigcap D(x)} f_{X|Y}(x|y_0)dx Xnew∼fX∣Y(x∣y)=⎩⎪⎨⎪⎧fY(y0)f(x,y0),0,x∈[a(y0),b(y0)]othersP(X∈G∣Y=y0)=G⋂D(x)∫fX∣Y(x∣y0)dx
例题 color{White}colorbox{Fuchsia}{例题} 例题:随机变量 ( X , Y ) (X,Y) (X,Y) 的概率密度为 f ( x , y ) = { 1 , ∣ y ∣ < x , 0 < x < 1 0 , o t h e r s f(x,y)=begin{cases}begin{aligned}&1,&&|y|<x,0<x<1\ &0,&&othersend{aligned}end{cases} f(x,y)={1,0,∣y∣<x,0<x<1others
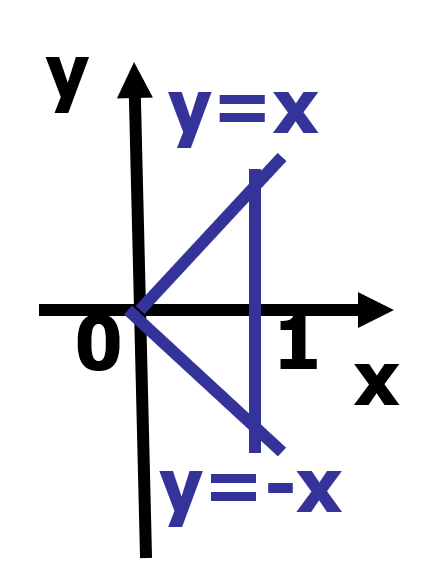
-
求 f X ( x ) , f Y ( y ) f_X(x),f_Y(y) fX(x),fY(y)
解:
f X ( x ) = ∫ − ∞ + ∞ f ( x , y ) d y = { ∫ − x x d y = 2 x , 0 < x < 1 0 , o t h e r s f_X(x)=int_{-infty}^{+infty}f(x,y)dy=begin{cases}begin{aligned}&int_{-x}^xdy=2x,&&0<x<1 \ &0,&&othersend{aligned}end{cases}\ fX(x)=∫−∞+∞f(x,y)dy=⎩⎪⎨⎪⎧∫−xxdy=2x,0,0<x<1othersf Y ( y ) = ∫ − ∞ + ∞ f ( x , y ) d x = { ∫ y 1 d x = 1 − y , 0 ≤ y < 1 ∫ − y 1 d x = 1 + y , − 1 ≤ y < 0 0 , o t h e r s = { 1 − ∣ y ∣ , ∣ y ∣ < 1 0 , o t h e r s f_Y(y)=int_{-infty}^{+infty}f(x,y)dx=begin{cases}begin{aligned}&int_{y}^1dx=1-y,&&0le y<1 \&int_{-y}^1dx=1+y,&&-1le y< 0\&0,&&othersend{aligned}end{cases}=begin{cases}1-|y|,|y|<1\0,others end{cases} fY(y)=∫−∞+∞f(x,y)dx=⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∫y1dx=1−y,∫−y1dx=1+y,0,0≤y<1−1≤y<0others={1−∣y∣,∣y∣<10,others
-
求 f X ∣ Y ( x ∣ y ) , f Y ∣ X ( y ∣ x ) f_{X|Y}(x|y),f_{Y|X}(y|x) fX∣Y(x∣y),fY∣X(y∣x)
解:
当 ∣ y ∣ < 1 时 f X ∣ Y ( x ∣ y ) = f ( x , y ) f Y ( y ) = { 1 1 − ∣ y ∣ , ∣ y ∣ < x < 1 0 , o t h e r s 当 0 < y < 1 时 f Y ∣ X ( y ∣ x ) = f ( x , y ) f X ( x ) = { 1 2 x , ∣ y ∣ < x 0 , o t h e r s begin{aligned}&当|y|<1时\ & f_{X|Y}(x|y)=dfrac{f(x,y)}{f_Y(y)}=begin{cases}&dfrac{1}{1-|y|},&|y|<x<1\&0,&others end{cases}\ &当0<y<1时\ & f_{Y|X}(y|x)=dfrac{f(x,y)}{f_X(x)}=begin{cases}&dfrac{1}{2x},&|y|<x\&0,&others end{cases}end{aligned} 当∣y∣<1时fX∣Y(x∣y)=fY(y)f(x,y)=⎩⎨⎧1−∣y∣1,0,∣y∣<x<1others当0<y<1时fY∣X(y∣x)=fX(x)f(x,y)=⎩⎨⎧2x1,0,∣y∣<xothers -
求 P { Y > 1 4 ∣ X = 1 2 } P{Y>dfrac{1}{4}|X=dfrac{1}{2}} P{Y>41∣X=21}
当 x = 1 2 时 , f Y ∣ X ( y ∣ 1 2 ) = { 1 , ∣ y ∣ < 1 2 0 , o t h e r s P { Y > 1 4 ∣ X = 1 2 } = ∫ 1 4 1 2 1 d y = 1 4 begin{aligned}&当x=dfrac{1}{2}时, f_{Y|X}(y|dfrac{1}{2})=begin{cases}1,quad|y|<dfrac{1}{2}\0,quad others end{cases}\ &P{Y>dfrac{1}{4}|X=dfrac{1}{2}}=int_{1over 4}^{1over 2}1;dy=dfrac{1}{4} end{aligned} 当x=21时,fY∣X(y∣21)=⎩⎨⎧1,∣y∣<210,othersP{Y>41∣X=21}=∫41211dy=41
3.4 二维随机变量函数的分布
-
二维离散型随机变量函数:若 P { X = x i , Y = y i } = p i j P{X=x_i,Y=y_i}=p_{ij} P{X=xi,Y=yi}=pij,则 Z = g ( X , Y ) Z=g(X,Y) Z=g(X,Y) 有分布律 P ( Z = z k ) = ∑ g ( x i , y j ) = z k p i j color{red}P(Z=z_k)=sumlimits_{g(x_i,y_j)=z_k}p_{ij} P(Z=zk)=g(xi,yj)=zk∑pij
-
二维连续型随机变量函数: Z = g ( X , Y ) Z=g(X,Y) Z=g(X,Y) 是随机变量, f ( x , y ) f(x,y) f(x,y) 一般定义域简洁(例如矩形)
-
求随机变量函数 Z = g ( X , Y ) Z=g(X,Y) Z=g(X,Y) 的密度函数的一般方法:
-
⨀ color{red}bigodot ⨀ 1.确定 Z Z Z 的取值范围 R ( Z ) R(Z) R(Z);
-
⨀ color{red}bigodot ⨀ 2.求 Z Z Z 的分布函数,对任意 z ∈ R ( Z ) zin R(Z) z∈R(Z),先求 Z Z Z 的分布函数
F Z ( z ) = P { Z ≤ z } = P { g ( X , Y ) ≤ z } = P { ( X , Y ) ∈ G ( z ) } = ∫ ( x , y ) ∈ G ( z ) ⋂ D f ( x , y ) d x d y color{red}F_Z(z)=P{Zle z}=P{g(X,Y)le z}=P{(X,Y)in G(z)}=intlimits_{(x,y)in G(z)bigcap D}f(x,y);dxdy FZ(z)=P{Z≤z}=P{g(X,Y)≤z}=P{(X,Y)∈G(z)}=(x,y)∈G(z)⋂D∫f(x,y)dxdy -
⨀ color{red}bigodot ⨀ 3.再求密度 f Z ( z ) = { F Z ′ ( z ) , z ∈ R ( Z ) 0 , z ∉ R ( Z ) f_Z(z)=begin{cases}begin{aligned}&color{red}F_Z'(z),&zin R(Z)\ &0,&znotin R(Z) end{aligned}end{cases} fZ(z)={FZ′(z),0,z∈R(Z)z∈/R(Z)
注意事项:
- 先画 ( x , y ) (x,y) (x,y) 定义域 D D D,再画 G ( z ) G(z) G(z)(一簇曲线),考虑 G ( z ) ⋂ D G(z)bigcap D G(z)⋂D 的形式
- 解释积分限,与 z z z 有关
-
-
例题 color{White}colorbox{Fuchsia}{例题} 例题:已知 ( X , Y ) (X,Y) (X,Y) 有密度函数 f ( x , y ) = { x y , 0 ≤ x ≤ 2 , 0 ≤ y ≤ 1 0 , o t h e r s f(x,y)=begin{cases}begin{aligned}&xy,&0le xle 2,0le yle 1\ &0,&others end{aligned}end{cases} f(x,y)={xy,0,0≤x≤2,0≤y≤1others,求 Z = X Y Z=XY Z=XY 的密度函数。
解:
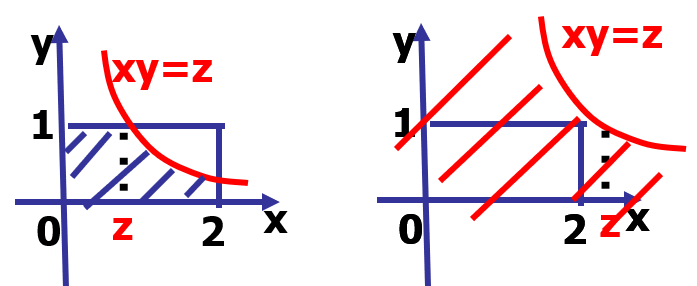
易 得 R ( Z ) = [ 0 , 2 ] ; 对 于 ∀ z ∈ [ 0 , 2 ] , 有 F Z ( z ) = P ( Z ≤ z ) = P ( X Y ≤ Z ) . 当 z ∈ [ 0 , 2 ] 时 , F Z ( z ) = ∬ D ⋂ G f ( x , y ) d x d y = ∫ 0 z d x ∫ 0 1 x y d y + ∫ z 2 d x ∫ 0 z x x y d y = z 2 4 + z 2 2 ( ln 2 − ln z ) ; 当 y ∈ ( 2 , + ∞ ) 时 , F Z ( z ) = 1 ; 当 y ∈ ( − ∞ , 0 ) 时 , F Z ( z ) = 0. 从 而 f Z ( z ) = F Z ′ ( z ) = { z ( ln 2 − ln z ) , 0 ≤ z ≤ 2 0 , o t h e r s begin{aligned}&易得R(Z)=[0,2];&&对于forall zin[0,2], 有F_Z(z)=P(Zle z)=P(XYle Z).\ &当zin[0,2]时, &&F_Z(z)=iintlimits_{Dbigcap G}f(x,y);dxdy = int_0^zdxint_0^1xydy+int_z^2dxint_0^dfrac{z}{x}xydy = dfrac{z^2}{4}+dfrac{z^2}{2}(ln2-ln z);\ &当yin(2,+infty)时, &&F_Z(z)= 1;\ &当yin(-infty,0)时, &&F_Z(z)= 0.\ end{aligned}\ 从而f_Z(z)=F_Z'(z) =begin{cases}z(ln2-ln z),0le zle2\0,others end{cases} 易得R(Z)=[0,2];当z∈[0,2]时,当y∈(2,+∞)时,当y∈(−∞,0)时,对于∀z∈[0,2],有FZ(z)=P(Z≤z)=P(XY≤Z).FZ(z)=D⋂G∬f(x,y)dxdy=∫0zdx∫01xydy+∫z2dx∫0xzxydy=4z2+2z2(ln2−lnz);FZ(z)=1;FZ(z)=0.从而fZ(z)=FZ′(z)={z(ln2−lnz),0≤z≤20,others
-
-
离散型 + 连续性: X X X 为离散型随机变量, Y Y Y 为连续型随机变量,求 Z = X Y Z=XY Z=XY 的密度
F Z ( z ) = ∑ i ∈ X P ( X i ) P ( Y ∣ X i ) color{red}F_Z(z)=sumlimits_{iin X} P(X_i)P(Y|X_i) FZ(z)=i∈X∑P(Xi)P(Y∣Xi) -
卷积公式(适用于 Z = X ± Y Z=Xpm Y Z=X±Y):二维连续性随机变量 ( X , Y ) (X,Y) (X,Y) 有联合密度 f ( x , y ) f(x,y) f(x,y),变量函数 Z = X + Y Z=X+Y Z=X+Y,则 Z Z Z 的密度函数为
f Z ( z ) = ∫ − ∞ + ∞ f ( x , z − x ) d x = ∫ − ∞ + ∞ f ( z − y , y ) d y color{red}f_Z(z)=int_{-infty}^{+infty} f(x,z-x);dx=int_{-infty}^{+infty} f(z-y,y);dy fZ(z)=∫−∞+∞f(x,z−x)dx=∫−∞+∞f(z−y,y)dy
特别地,当 X X X 与 Y Y Y 相互独立时,有
f Z ( z ) = ∫ − ∞ + ∞ f X ( x ) f Y ( z − x ) d x = ∫ − ∞ + ∞ f X ( z − y ) f Y ( y ) d y color{red}f_Z(z)=int_{-infty}^{+infty} f_X(x)f_Y(z-x);dx=int_{-infty}^{+infty} f_X(z-y)f_Y(y);dy fZ(z)=∫−∞+∞fX(x)fY(z−x)dx=∫−∞+∞fX(z−y)fY(y)dy- 证明:
F Z ( z ) = P { Z ≤ z } = P { X + Y ≤ z } = ∬ x + y ≤ z f ( x , y ) d x d y = ∫ − ∞ + ∞ d x ∫ − ∞ z − x f ( x , y ) d y 令 u = y + x , 则 d y = d u , 故 F Z ( z ) = ∫ − ∞ + ∞ d x ∫ − ∞ z f ( x , u − x ) d u = ∫ − ∞ z [ ∫ − ∞ + ∞ f ( x , u − x ) d x ] d u 从 而 f Z ( z ) = F Z ′ ( z ) = ∫ − ∞ + ∞ f ( x , z − x ) d x begin{aligned}&F_Z(z)=P{Zle z}=P{X+Yle z}=iintlimits_{x+yle z}f(x,y);dxdy=int_{-infty}^{+infty}dxint_{-infty}^{z-x}f(x,y);dy\ &令u=y+x,则dy=du,故 \ &F_Z(z)=int_{-infty}^{+infty}dxint_{-infty}^{z}f(x,u-x);du=int_{-infty}^zleft[int_{-infty}^{+infty}f(x,u-x)dx right]du \ &从而f_Z(z)=F'_Z(z)=int_{-infty}^{+infty} f(x,z-x)dx end{aligned} FZ(z)=P{Z≤z}=P{X+Y≤z}=x+y≤z∬f(x,y)dxdy=∫−∞+∞dx∫−∞z−xf(x,y)dy令u=y+x,则dy=du,故FZ(z)=∫−∞+∞dx∫−∞zf(x,u−x)du=∫−∞z[∫−∞+∞f(x,u−x)dx]du从而fZ(z)=FZ′(z)=∫−∞+∞f(x,z−x)dx
-
例题 color{White}colorbox{Fuchsia}{例题} 例题:已知 ( X , Y ) (X,Y) (X,Y) 有密度函数 f ( x , y ) = { 2 − x − y , 0 < x , y < 1 0 , o t h e r s f(x,y)=begin{cases}begin{aligned}&2-x-y,&0<x,y< 1\ &0,&others end{aligned}end{cases} f(x,y)={2−x−y,0,0<x,y<1others,求 Z = X + Y Z=X+Y Z=X+Y 的密度函数。
解:
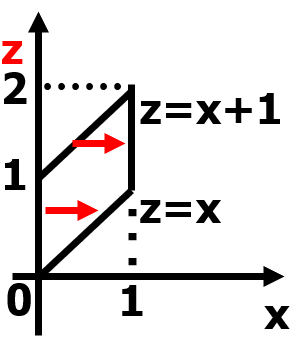
R ( Z ) = ( 0 , 2 ) , 对 ∀ 0 < z < 2 , 有 f Z ( z ) = ∫ ∞ + ∞ f ( x , z − x ) d x . 使 被 积 函 数 f ( x , z − x ) 非 零 , 需 满 足 { 0 < x < 1 0 < z − x < 1 , 即 { 0 < x < 1 x < z < 1 + x 当 0 < z < 1 时 , f Z ( z ) = ∫ 0 z ( 2 − z ) d x = z ( 2 − z ) 当 1 < z < 2 时 , f Z ( z ) = ∫ z − 1 1 ( 2 − z ) d x = ( 2 − z ) 2 f Z ( z ) = { z ( 2 − z ) , 0 < z < 1 ( 2 − z ) 2 , 1 < z < 2 0 , o t h e r s begin{aligned}&R(Z)=(0,2),对forall 0<z<2,有f_Z(z)=int_{infty}^{+infty}f(x,z-x);dx.\ &使被积函数f(x,z-x)非零,需满足color{red}begin{cases}0<x<1\0<z-x<1end{cases},即begin{cases}0<x<1\x<z<1+xend{cases}\ &当0<z<1时,f_Z(z)=int_0^z(2-z)dx=z(2-z)\ &当1<z<2时,f_Z(z)=int_{z-1}^1 (2-z)dx=(2-z)^2\ &f_Z(z)=begin{cases}z(2-z),0<z<1 \(2-z)^2,1<z<2\0,othersend{cases} end{aligned} R(Z)=(0,2),对∀0<z<2,有fZ(z)=∫∞+∞f(x,z−x)dx.使被积函数f(x,z−x)非零,需满足{0<x<10<z−x<1,即{0<x<1x<z<1+x当0<z<1时,fZ(z)=∫0z(2−z)dx=z(2−z)当1<z<2时,fZ(z)=∫z−11(2−z)dx=(2−z)2fZ(z)=⎩⎪⎨⎪⎧z(2−z),0<z<1(2−z)2,1<z<20,others
-
常见分布可加性( n n n 维随机变量):
-
二项分布:若 X i X_i Xi 之间相互独立,且 X i ∼ B ( n i , p ) , i = 1 , 2 , . . . , n X_isim B(n_i,p),i=1,2,...,n Xi∼B(ni,p),i=1,2,...,n,则 X 1 + X 2 + . . . X n ∼ B ( ∑ i = 1 n n i , p ) color{red}X_1+X_2+...X_nsim B(sumlimits_{i=1}^n n_i,p) X1+X2+...Xn∼B(i=1∑nni,p)
证明:离散型 Z = X + Y Z=X+Y Z=X+Y 有 P ( Z = k ) = ∑ i = 0 k P ( X = i , Y = k − i ) = ∑ i = 0 k P ( X = i ) P ( Y = k − i ) P(Z=k)=sumlimits_{i=0}^k P(X=i,Y=k-i)=sumlimits_{i=0}^k P(X=i)P(Y=k-i) P(Z=k)=i=0∑kP(X=i,Y=k−i)=i=0∑kP(X=i)P(Y=k−i)
-
泊松分布:若 X i X_i Xi 之间相互独立,且 X i ∼ P ( λ i ) , i = 1 , 2 , . . . , n X_isim P(lambda_i),i=1,2,...,n Xi∼P(λi),i=1,2,...,n,则 X 1 + X 2 + . . . X n ∼ P ( ∑ i = 1 n λ i ) color{red}X_1+X_2+...X_nsim P(sumlimits_{i=1}^n lambda_i) X1+X2+...Xn∼P(i=1∑nλi)
-
Γ Gamma Γ 分布:若 X i X_i Xi 之间相互独立,且 X i ∼ Γ ( α i , β ) , i = 1 , 2 , . . . , n X_isim Gamma(alpha_i,beta),i=1,2,...,n Xi∼Γ(αi,β),i=1,2,...,n,则 X 1 + X 2 + . . . X n ∼ Γ ( ∑ i = 1 n α i , β ) color{red}X_1+X_2+...X_nsim Gamma(sumlimits_{i=1}^n alpha_i,beta) X1+X2+...Xn∼Γ(i=1∑nαi,β)
-
-
极大值极小值分布( n n n 维随机变量):若 X i X_i Xi 之间相互独立,且 X i X_i Xi 有分布函数 F i ( x i ) , i = 1 , 2 , . . . , n F_i(x_i),i=1,2,...,n Fi(xi),i=1,2,...,n。令 M = max { X i , X 2 , . . . , X n } , N = min { X i , X 2 , . . . , X n } M=max{X_i,X_2,...,X_n},N=min{X_i,X_2,...,X_n} M=max{Xi,X2,...,Xn},N=min{Xi,X2,...,Xn},则 M , N M,N M,N 的分布函数为
F M ( x ) = P ( max i = 1 n { X i } ≤ x ) = P ( ⋂ i = 1 n X i ≤ x ) = ∏ i = 1 n P ( X i ≤ x ) = ∏ i = 1 n F i ( x ) F N ( x ) = P ( min i = 1 n { X i } ≤ x ) = 1 − P ( min i = 1 n { X i } > x ) = 1 − P ( ⋂ i = 1 n X i > x ) = 1 − ∏ i = 1 n P ( X i > x ) = 1 − ( ∏ i = 1 n 1 − F i ( x ) ) begin{aligned}F_M(x)&=P(maxlimits_{i=1}^n {X_i}le x)\ &=P(bigcaplimits_{i=1}^n X_ile x)\ &=prodlimits_{i=1}^n P(X_ile x)\ &=color{red}prodlimits_{i=1}^n F_i(x)\ F_N(x)&=P(minlimits_{i=1}^n {X_i}le x)\ &=1-P(minlimits_{i=1}^n {X_i}> x)\ &=1-P(bigcaplimits_{i=1}^n X_i>x)\ &=1-prodlimits_{i=1}^n P(X_i> x)\ &=color{red}1-left(prodlimits_{i=1}^n 1-F_i(x)right)\ end{aligned} FM(x)FN(x)=P(i=1maxn{Xi}≤x)=P(i=1⋂nXi≤x)=i=1∏nP(Xi≤x)=i=1∏nFi(x)=P(i=1minn{Xi}≤x)=1−P(i=1minn{Xi}>x)=1−P(i=1⋂nXi>x)=1−i=1∏nP(Xi>x)=1−(i=1∏n1−Fi(x))
特别地,若 X i X_i Xi 之间独立同分布 i.i.d., 则
{ F M ( x ) = F n ( x ) F N ( x ) = 1 − [ 1 − F ( x ) ] n { f M ( x ) = [ F n ( x ) ] ′ = n F n − 1 ( x ) f ( x ) f N ( x ) = [ 1 − [ 1 − F ( x ) ] n ] ′ = n [ 1 − F ( X ) ] n − 1 f ( x ) begin{cases}F_M(x)=color{red}F^n(x)\ F_N(x)=color{red}1-[1-F(x)]^nend{cases}qquad begin{cases}f_M(x)=[F^n(x)]'=color{red}nF^{n-1}(x)f(x)\ f_N(x)=[1-[1-F(x)]^n]'=color{red}n[1-F(X)]^{n-1}f(x) end{cases} {FM(x)=Fn(x)FN(x)=1−[1−F(x)]n{fM(x)=[Fn(x)]′=nFn−1(x)f(x)fN(x)=[1−[1−F(x)]n]′=n[1−F(X)]n−1f(x)例如:并联系统为极大值分布,串联系统为极小值分布
最后
以上就是健忘皮皮虾最近收集整理的关于第三章 多维随机变量及其分布(概率论)第三章 多维随机变量及其分布的全部内容,更多相关第三章内容请搜索靠谱客的其他文章。








发表评论 取消回复