哈夫曼压缩与解压缩
目录
哈夫曼压缩与解压缩
一:引言
二:主要技术点
三:过程介绍
1、压缩:
2、解压缩
四:详细分析
一:准备过程
二:压缩
三:解压缩
五:结果演示
六:总结
七:源码地址
一:引言
之前的两个贪吃蛇和巨大数的练习,总体来说难度不大,有好的算法和比较新颖的微译码补码。但是,哈夫曼压缩与解压缩可以说难度比前两个大得多,涉及的知识面更加广。做完这个,是对自己基本功的检测,更能提升自己的编程能力。
hffman编码的思想对文件进行压缩,主要原理是通过huffman编码来重新表示字符,使得出现频率高的字符编码短,出现少的字符编码长。整体下来的话,所需的总的bit位是减少的。但是要注意当大部分字符出现的频率都差不多时,huffman压缩的压缩效率会很低。
编程环境:
UE(或sublime),TDM-GCC。
二:主要技术点
- 文件的各种操作
- 递归思想构造哈夫曼编码。
- 位运算思想进行压缩与解压缩。
- 自定义目标压缩文件头部元数据。
- 主函数带参,命令行参数。
三:过程介绍
1、压缩:
1、统计字符种类及频度:ASCII码值当下标,字符频度当对应下标的值。
2、构建哈夫曼树:在没有访问过的节点中,找最小字符频度下标来构建哈夫曼树。
3、构建哈夫曼编码:递归思想构建。
4、生成压缩文件(.ycyHuf后缀名):把字符的哈夫曼编码以二进制形式写入目标文件中。给压缩文件头部写入元数据,解压缩时需使用这些数据。
注意事项:给目标文件写二进制数据时,最后一个字节如果不满八位,会产生垃圾数据,如果不进行处理,在解压后,就不能完整的还原。所以,需计算最后一个字节中的有效位数。
2、解压缩
1、根据压缩文件的头部元数据,得到字符种类和频度。
2、构建哈夫曼树:在没有访问过的节点中,找最小字符频度下标来构建哈夫曼树。
3、构建哈夫曼编码:递归思想构建。
4、生成解压缩的文件(后缀名和源文件后缀名一样 )即可:一位一位的从压缩文件中读取信息,'1'向左子树走,'0'向右子树走。
注意事项:压缩文件头部有元数据,所以,解压时需要把文件指针定位到真正的信息处。当碰到最后一字节的垃圾位时,应结束,否则解压出的信息和源文件会不匹配。
四:详细分析
一:准备过程
三个关于位运算的宏

1、取出index位,若取出的index位为0,则GET_BYTE值为假,否则为真
#define GET_BYTE(vbyte, index) (((vbyte) & (1 << ((index) ^ 7))) != 0)
2、把index位设置为‘1’
#define SET_BYTE(vbyte, index) ((vbyte) |= (1 << ((index) ^ 7)))
3、把index位设置为‘0’
#define CLR_BYTE(vbyte, index) ((vbyte) &= (~(1 << ((index) ^ 7))))
二:压缩
1、统计字符种类和频度
结构体定义:
typedef struct ALPHA_FREQ {
unsigned char alpha; //字符,考虑到文件中有汉字,所以定义成unsigned char
int freq; //字符出现的频度
} ALPHA_FREQ;代码分析:
ALPHA_FREQ *getAlphaFreq(char *sourceFileName, int *alphaVariety) {
int freq[256] = {0};
int i;
int index;
ALPHA_FREQ *alphaFreq = NULL;
FILE *fpIn;
int ch;
fpIn = fopen(sourceFileName, "rb");
/*统计所有字符的频度*/
ch = fgetc(fpIn);
while(!feof(fpIn)) {
freq[ch]++;
ch = fgetc(fpIn);
}
fclose(fpIn);
/*统计所有字符的种类*/
for(i = 0; i < 256; i++) {
if(freq[i]) {
(*alphaVariety)++;
}
}
alphaFreq = (ALPHA_FREQ *) calloc(sizeof(ALPHA_FREQ), *alphaVariety);
for(i = index = 0; i < 256; i++) {
if(freq[i]) {
alphaFreq[index].alpha = i;
alphaFreq[index].freq = freq[i];
index++;
}
}
return alphaFreq;
}统计字符及其频度,开始想到了一个笨办法。 如下:
AlPHA_FREQ freq[256]
count = 0;
i = 0;
while(str[i]) {
index = 0;
while(index < count) {
if(freq[index].alpha == str[i]) {
break;
}
index++
}
if(index < count) {
freq[count].freq++;
} else {
freq[count].alpha = str[i];
freq[count].freq = 1;
count++;
}
}但是,这样做有一个很大的缺点:随着字符串的增多,查找次数就会越来越多,极端情况下,没有重复的字符,那么就要执行n-1次,光一个统计字符的函数,其时间复杂度就达到了O(n^2);这显然是不合理的。因此,有一个更好的算法:构建一个大的数组,以字符的ASCII码值当下标,字符频度当对应下标的值,实现用空间,换时间的目的。例如'A'的频度,永远存放在下标为65的元素中。这样做,其时间复杂度达到了O(n)。
2、初始化哈夫曼表
结构体定义:
typedef struct HUFFMAN_TAB {
ALPHA_FREQ alphaFreq;
int leftChild;
int rightChild;
boolean visited;
char *code;
} HUFFMAN_TAB;HUFFMAN_TAB *initHuffmanTab(ALPHA_FREQ *alphaFreq, int alphaVariety, int *hufIndex) {
int i;
HUFFMAN_TAB *huffmanTab = NULL;
huffmanTab = (HUFFMAN_TAB *) calloc(sizeof(HUFFMAN_TAB), 2 * alphaVariety - 1);
//huffmanTab申请了 2 * alphaVariety - 1大小的空间,在这只用了 alphaVariety个,还剩alphaVariety - 1个
for(i = 0; i < alphaVariety; i++) {
hufIndex[alphaFreq[i].alpha] = i; //把哈夫曼表中的字符和其对应的下标形成键值对,存到hufIndex中
huffmanTab[i].alphaFreq = alphaFreq[i];
huffmanTab[i].leftChild = huffmanTab[i].rightChild = -1;
huffmanTab[i].visited = FALSE;
huffmanTab[i].code = (char *) calloc(sizeof(char), alphaVariety);
}
return huffmanTab;
}字符种类个数即为哈夫曼树的叶子结点个数,那么,根据完全二叉树的性质,这个哈夫曼树的总结点数为叶子节点数加度为2的节点数,所以,n总 = 2 * n0 - 1。先构建出哈夫曼表,为后面构建哈夫曼树做准备。注意,需设置一个visited成员来表示结点有没有被访问过。
例如:字符串为“siytweusitweusitweusitwesitesitesitesieieieeeeee”,那么,统计出的结果为这样:
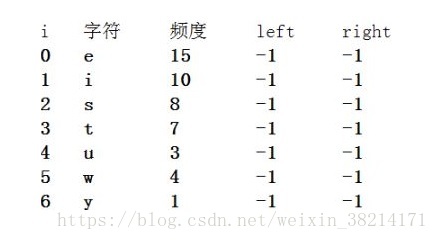
根据这个哈夫曼表,可以画出哈夫曼树的结构了,如下:
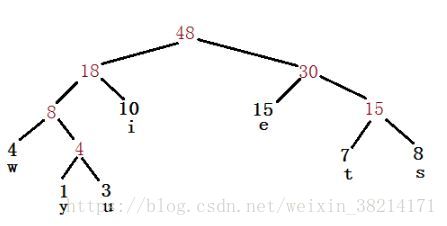
3、生成哈夫曼树
生成哈夫曼树,我们需要把频度大的节点放在离根近的地方,频度小的节点放在离根远的地方。所以,需要进行最小字符频度的查找。
int getMinFreq(HUFFMAN_TAB *huffmanTab, int count) {
int index;
int minIndex = NOT_INIT;
for(index = 0; index < count; index++) {
if(FALSE == huffmanTab[index].visited) {
if(NOT_INIT == minIndex || huffmanTab[index].alphaFreq.freq < huffmanTab[minIndex].alphaFreq.freq) {
minIndex = index;
}
}
}
huffmanTab[minIndex].visited = TRUE;
return minIndex;
}void creatHuffmanTree(HUFFMAN_TAB *huffmanTab, int alphaVariety) {
int i;
int leftChild;
int rightChild;
//huffmanTab使用剩下的 alphaVariety - 1个空间
for(i = 0; i < alphaVariety - 1; i++) {
leftChild = getMinFreq(huffmanTab, alphaVariety + i);
rightChild = getMinFreq(huffmanTab, alphaVariety + i);
huffmanTab[alphaVariety + i].alphaFreq.alpha = '#';
huffmanTab[alphaVariety + i].alphaFreq.freq = huffmanTab[leftChild].alphaFreq.freq
+ huffmanTab[rightChild].alphaFreq.freq;
huffmanTab[alphaVariety + i].leftChild = leftChild;
huffmanTab[alphaVariety + i].rightChild = rightChild;
huffmanTab[alphaVariety + i].visited = FALSE;
}
}生成的哈夫曼树的表格形式如下
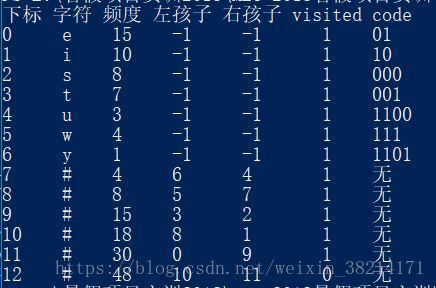
4、生成哈夫曼编码
哈夫曼树都已经生成,那么就需要生成哈夫曼编码了。
思路:需要把哈夫曼树从根节点除法,进行遍历,向左子树为‘1’,右子树为‘0’;若碰到叶子结点,需要把编码存给对应的字符。若没有碰到叶子结点,则需要继续向下遍历。所以,这需要一个递归程序完成。
void makeHuffmanCode(HUFFMAN_TAB *huffmanTab, int root, int index, char *code) {
if(huffmanTab[root].leftChild != -1 && huffmanTab[root].rightChild != -1) {
code[index] = '1';
makeHuffmanCode(huffmanTab, huffmanTab[root].leftChild, index + 1, code);
code[index] = '0';
makeHuffmanCode(huffmanTab, huffmanTab[root].rightChild, index + 1, code);
} else {
code[index] = 0;
strcpy(huffmanTab[root].code, code);
}
}5、把哈夫曼编码以二进制位形式写入目标文件中
此时,我们需要考虑一个问题。如果,光把“siytweusitweusitweusitwesitesitesitesieieieeeeee”这个字符串的哈夫曼编码以二进制形式写入目标文件,形成的目标文件中全是0101这种二进制代码,那如何解密呢?没有人能看懂这种二进制代码,所以,我们需要给目标文件的头部写入元数据(解释数据的数据),这些元数据主要包括源文件字符种类,字符频度。有了元数据,那么,就可以在解压缩程序中再构造一个完全相同的哈夫曼树,完成解压缩。
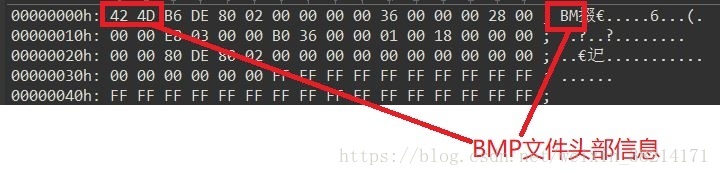
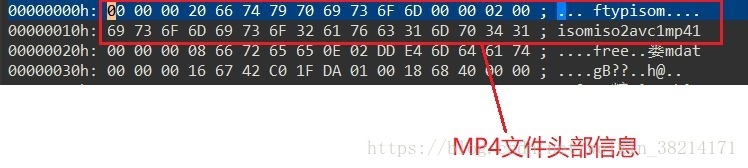
所以,我们也可以构造我们的文件头部元数据,定义一个结构体如下:
typedef struct HUF_FILE_HEAD {
unsigned char flag[3]; //压缩二进制文件头部标志 ycy
unsigned char alphaVariety; //字符种类
unsigned char lastValidBit; //最后一个字节的有效位数
unsigned char unused[11]; //待用空间
} HUF_FILE_HEAD; //这个结构体总共占用16个字节的空间依次给文件头部写入头部标志“ycy”, 字符种类alphaVariety, 最后一字节的有效位数lastValidBit。
HUF_FILE_HEAD fileHead = {'y', 'c', 'y'};
fileHead.alphaVariety = (unsigned char) alphaVariety;
fileHead.lastValidBit = getlastValidBit(huffmanTab, alphaVariety);
fwrite(&fileHead, sizeof(HUF_FILE_HEAD), 1, fpOut);
fwrite(alphaFreq, sizeof(ALPHA_FREQ), alphaVariety, fpOut);lastValidBit计算过程:
//取最后一个字节的有效位数
int getlastValidBit(HUFFMAN_TAB *huffmanTab, int alphaVariety) {
int sum = 0;
int i;
for(i = 0; i < alphaVariety; i++) {
sum += strlen(huffmanTab[i].code) * huffmanTab[i].alphaFreq.freq;
//如果不执行这一步,当数据长度超过int的表示范围,就会出错
sum &= 0xFF; //0xFF化为二进制位1111 1111,这样做sum始终是最后一个字节,8位
}
//举例:若最后生成7位二进制,划分为一个字节,那么,这一个字节只有7位为有效位,其余都是垃圾位。
//我们只需要取出这个字节的那7个有效位,所以sum和8取余即可
//sum = sum % 8 <=> sum = sum & 0x7
//返回最后一个字节的有效位数
sum &= 0x7;
return sum == 0 ? 8 : sum;
}完后,我们的.ycyHuf文件头部就写好了:
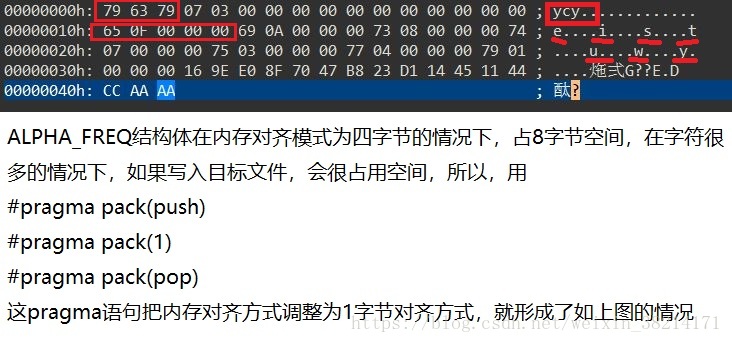
头部元数据写好后,就需要写入真正的压缩信息了。但是,如何根据字符,迅速找到其哈夫曼编码呢?有一种笨办法,就是每次都根据当前字符,在哈夫曼表中查找,如果字符匹配,就找到了哈夫曼编码。
for(i = 0; i < alphaVariety; i++) {
if(str[index] == huffmanTab[i]) {
hufCode = huffmanTab[i].code;
}
}但是,这样每次查找进行的比较次数平均为n / 2,若字符串长度为len,则时间复杂度为O(len * n / 2)。所以,这样做不是很好,有一种方法,可以不进行“查找”,就能“查找到”,时间复杂度为O(1); 这样,需要构造出一个“字符”:“下标”的键值对关系,字符可以直接定位,就完成了这个“迅速查找”的任务。所以,我在初始化哈夫曼表initHuffmanTab()函数中,构造了这个键值对关系。
//构造键值对
hufIndex[alphaFreq[i].alpha] = i; //把哈夫曼表中的字符和其对应的下标形成键值对,存到hufIndex中
//查找
hufCode = huffmanTab[hufIndex[ch]].code;下来,就可以正式的给目标压缩文件中写数据了。
ch = fgetc(fpIn);
while(!feof(fpIn)) {
hufCode = huffmanTab[hufIndex[ch]].code;
//把每个字符的哈夫曼编码一个一个过。
//如果是字符'0',就转换为二进制的0
//如果是字符'1',就转换为二进制的1
for(i = 0; hufCode[i]; i++) {
if('0' == hufCode[i]) {
//value为一个字节
//从第1位依次赋值,若大于八位(一个字节)了,就写入文件中
CLR_BYTE(value, bitIndex);
} else {
SET_BYTE(value, bitIndex);
}
bitIndex++;
if(bitIndex >= 8) {
bitIndex = 0;
fwrite(&value, sizeof(unsigned char), 1, fpOut);
}
}
ch = fgetc(fpIn);
}
//如果最后一次不满一个字节,依然需要写到文件中,注意:写入的最后一个字节可能会存在垃圾位
if(bitIndex) {
fwrite(&value, sizeof(unsigned char), 1, fpOut);
}如果遇到了字符‘0’,就利用位运算转换为二进制0,否则,为二进制1。 如果最后一次不满一个字节,依然需要写到文件中,注意:写入的最后一个字节可能会存在垃圾位。
三:解压缩
1、统计字符种类和频度
直接从压缩的文件中的头部读取。先匹配是不是自定义的格式:
fileHead = readFileHead(sourceFileName);
if(!(fileHead.flag[0] == 'y' && fileHead.flag[1] == 'c' && fileHead.flag[2] == 'y')) {
printf("不可识别的文件格式n");
}如果是“ycy”,那么再统计字符种类和频度:
ALPHA_FREQ *getAlphaFreq(char *sourceFileName, int *alphaVariety, HUF_FILE_HEAD fileHead) {
int freq[256] = {0};
int i;
int index;
ALPHA_FREQ *alphaFreq = NULL;
FILE *fpIn;
int ch;
*alphaVariety = fileHead.alphaVariety;
alphaFreq = (ALPHA_FREQ *) calloc(sizeof(ALPHA_FREQ), *alphaVariety);
fpIn = fopen(sourceFileName, "rb");
//略过前16个字节的元数据
fseek(fpIn, 16, SEEK_SET);
fread(alphaFreq, sizeof(ALPHA_FREQ), *alphaVariety, fpIn);
fclose(fpIn);
return alphaFreq;
}2、初始化哈夫曼表
和压缩过程一样。
3、生成哈夫曼树
和压缩过程一样。
4、生成哈夫曼编码
和压缩过程一样。
5、从压缩文件中读取二进制信息,还原文件
应该先利用fseek()函数把文件指针跳过前面的元数据和字符种类及频度,定位到真正需要还原的地方。一位一位的进行判断,'1'向左子树走,'0'向右子树走;若到达叶子结点,向文件中写入叶子结点下标对应的字符。再回到根结点继续;若超过一个字节,8位,则需要读取下一个字节。
void huffmanDecoding(HUFFMAN_TAB *huffmanTab, char *sourceFileName, char *targetFileName, int alphaVariety, HUF_FILE_HEAD fileHead) {
int root = 2 * alphaVariety - 2;
FILE *fpIn;
FILE *fpOut;
boolean finished = FALSE;
unsigned char value;
unsigned char outValue;
int index = 0;
long fileSize;
long curLocation;
fpIn = fopen(sourceFileName, "rb");
fpOut = fopen(targetFileName, "wb");
fseek(fpIn, 0L, SEEK_END);
fileSize = ftell(fpIn); //文件总长度fileSize
fseek(fpIn, 16 + 5 * fileHead.alphaVariety, SEEK_SET); //略过前面16个字节的元数据,5字节的字符种类和频度
curLocation = ftell(fpIn);
//从根出发,'1'向左子树走,'0'向右子树走,若到达叶子结点,输出叶子结点下标对应的字符。再回到根结点继续。
fread(&value, sizeof(unsigned char), 1, fpIn);
while(!finished) {
if(huffmanTab[root].leftChild == -1 && huffmanTab[root].rightChild == -1) {
outValue = huffmanTab[root].alphaFreq.alpha;
fwrite(&outValue, sizeof(unsigned char), 1, fpOut);
if(curLocation >= fileSize && index >= fileHead.lastValidBit) {
break;
}
root = 2 * alphaVariety - 2;
}
//取出的一个字节从第一位开始看,'1'向左子树走,'0'向右子树走
//若超过一个字节,8位,则需要读取下一个字节
if(GET_BYTE(value, index)) {
root = huffmanTab[root].leftChild;
} else {
root = huffmanTab[root].rightChild;
}
if(++index >= 8) {
index = 0;
fread(&value, sizeof(unsigned char), 1, fpIn);
curLocation = ftell(fpIn);
}
}
fclose(fpIn);
fclose(fpOut);
}五:结果演示
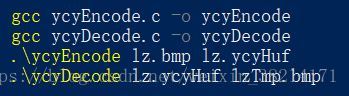
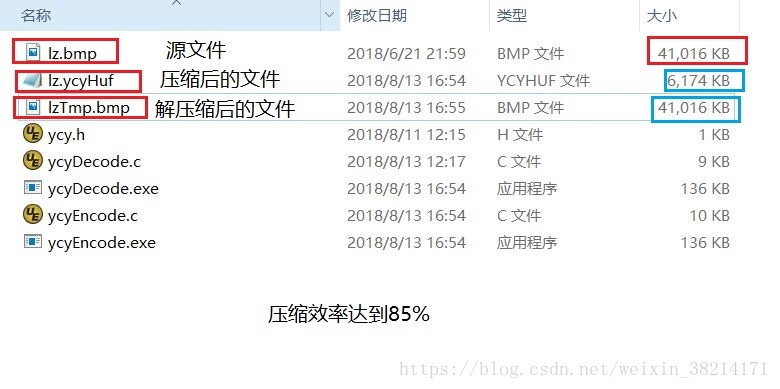
六:总结
哈夫曼压缩与解压缩的项目完成了(以后还会继续完善,优化)。这个项目涉及了C语言里更加高级的操作(文件,位运算,主函数带参······)。哈夫曼压缩与解压缩涉及的知识是我目前以来接触的项目里最多,最广的,收获很多。经过这个练习,还是觉得写程序前,一定一定要认真,仔细的进行手工过程的分析,一定要分析的很到位,否则,程序的逻辑就会出错,酿成大错。最后,不要忘记free申请的空间,以免造成内存泄漏。
七:源码地址
https://github.com/yangchaoy259189888/Huffman-compress/
纠错:
感谢下面这位前辈指出的这两个问题,经过测试,确实,当初测试了一个bmp文件,成功压缩和解压缩之后,以为大功告成。其实,还有很多极端情况没有考虑到。比如:一个全是a的txt文件就会失败。
本人能力有限,毕竟这个代码不是我一个人从头到尾完成的,其中的很多思想都来自教主。
还请看到的大神和我沟通,争取把这个错误解决······
最后
以上就是凶狠眼神最近收集整理的关于哈夫曼压缩与解压缩哈夫曼压缩与解压缩的全部内容,更多相关哈夫曼压缩与解压缩哈夫曼压缩与解压缩内容请搜索靠谱客的其他文章。





![[小项目]手把手教你C语言哈夫曼压缩/解压缩](https://www.shuijiaxian.com/files_image/reation/bcimg1.png)


发表评论 取消回复