LSTM解决梯度消失和爆炸情况

59 阅读 0 评论 39 点赞

我是靠谱客的博主心灵美薯片，最近开发中收集的这篇文章主要介绍LSTM解决梯度消失和爆炸情况，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

- - - - 1. LSTM避免RNN的梯度消失（gradient vanishing）
      - 2. LSTM避免RNN的梯度爆炸
      - 3. GRU 与 LSTM 比较
      - 4 Batch Normalization 到 Group Normalization
        Batch Normalization
        Group Normalization

1. LSTM避免RNN的梯度消失（gradient vanishing）

RNN的本质是在网络内部维护了一个状态 StSt，其中 tt 表示时间且 StSt 可递归计算。

传统的RNN总是用“覆写”的方式计算状态：St=f(St−1,xt)St=f(St−1,xt)，其中f(·)f(·)表示仿射变换外面在套一个Sigmoid， StSt 表示输入序列在时刻 tt的值。根据求导的链式法则，这种形式直接导致梯度被表示为连成积的形式，以致于造成梯度消失——粗略的说, 很多个小于1的项连乘就很快的逼近零。
现代的RNN（包括但不限于使用LSTM单元的RNN）使用“累加”的形式计算状态：
St=∑tτ=1ΔSτSt=∑τ=1tΔSτ，其中的 ΔΔ 显示依赖序列输入xtxt 稍加推导即可发现，这种累加形式导致导数也是累加形式，因此避免了梯度消失。
如长短期记忆（LSTM）与门控已经提出复发单元（GRU）来解决梯度问题。然而，双曲正切的使用Sigmoid函数作为激活函数这些变体导致在层上的梯度衰减。因此，深LSTM或GRU的建设与训练基于RNN的网络实际上是困难的。相比之下，IndRNN 使用非饱和激活函数等CNNsRelu可以被堆叠到非常深的网络中。使用基本卷积层和100层以上的层

2. LSTM避免RNN的梯度爆炸

设定阈值和使用正则化减少权重
爆炸梯度问题相对容易。

通过简单地收缩其规范超过的梯度来处理阈值，一种被称为梯度裁剪的技术。
如果一个巨大的因素减少了梯度，就会受到影响。过于频繁的裁剪是非常有效的。

3. GRU 与 LSTM 比较

GRU (Gated Recurrent Unit)

GRU与LSTM单元相似，GRU具有调节信息流动的门单元，但是，没有一个单独的记忆单元（memory cells）。
GRU在时刻 tt 的 激励 hjthtj 是一个线性的修改：hjt=(1−zjt)hjt−1+zjth̃ jthtj=(1−ztj)ht−1j+ztjh~tj

更新门的计算为 : zjt=σ(Wzxt+Uzht−1)jztj=σ(Wzxt+Uzht−1)j

这个过程是把现在的状态和新的状态求和，和LSTM的单元类似。GRU没有采取任何机制去控制那个状态暴露出来，而是每次所有状态都会暴露。

LSTM ( Long Short-Term Memory Unit)

一般的循环单元只是简单的计算输入信号的权重和一个非线性函数。

而LSTM每一个在t时刻的LSTM单元 jj 有一个记忆 cjtctj ,LSTM的输出或者激励是: hjt=ojttanh(cjt)htj=otjtanh(ctj)

GRC把LSTM的 input gate 和 forget gate 整合成一个update gate，也是通过gate机制来控制梯度。
除语言建模外，GRU（门控重复单元）在所有任务上都优于LSTM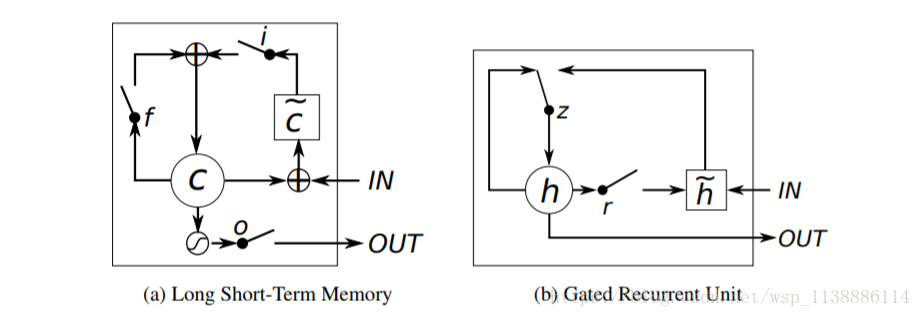
这里写图片描述

MUT1与GRU在语言建模方面的表现相匹配，在所有其他任务上均优于GRU
允许丢失时，LSTM在PTB上的性能明显优于其他体系结构
增加大忘记栅极偏置可大大提高LSTM性能
LSTM的遗忘门是最重要的，而输出门相对不重要一般初始化bais=0.5

4 Batch Normalization 到 Group Normalization

现在我们已经知道：

激活函数对梯度也有很大的影响，大部分激活函数只在某个区域内梯度比较好。
在后向传播的时候，我们需要进行链式求导，如果网络层很深，激活函数如果权重很小，会导致梯度消失；如果权重很大，又会导致梯度爆炸。

那么解决梯度消失可以从这几方面入手：
1）换激活函数；2）调整激活函数的输入；3）调整网络结构

事实上，我们有一个好东西可以解决梯度问题，叫做Normalization，就是从第二方面入手同时解决梯度消失和爆炸，而且也可以加快训练速度。

Batch Normalization

假设对于一个batch内某个维度的特征 x1,x2,...,xmx1,x2,...,xm，
BN需要将其转化成 y1,y2,...,ymy1,y2,...,ym，
首先对节点的线性组合值进行归一化，使其均值是0，方差是1。（也就是，对节点的输入进行归一化，而不是对输出进行归一化）（归一化后使梯度稳定,快速收敛）

x′i=xi−μσ2+ε‾‾‾‾‾‾√xi′=xi−μσ2+ε

其中 μμ 是均值，σ2σ2 是标准差，εε 是用来控制分母为正。

但是数据本来不是这样子的啊！我们强行对数据进行缩放，可能是有问题的，所以BN又加了一个scale的操作，使得数据有可能会恢复回原来的样子：

yi=γx′i+βyi=γxi′+β

加了scale可以提升模型的容纳能力。

既然是Batch归一化，那么BN就会受到batch size的影响：

如果size太小，算出的均值和方差就会不准确，影响归一化，导致性能下降，
如果太大，内存可能不够用。

Group Normalization

因此上个月提出的GN，就是为了避免batch size带来的影响。乍一看标题以为做了啥大改革，BN要退出舞台了，其实只是归一化的方向不一样，不再沿batch方向归一化，他们的不同点就在于归一化的方向不一样：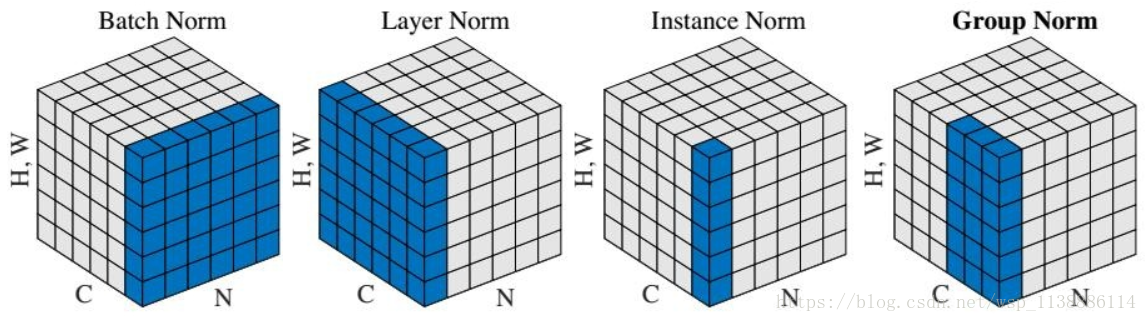
这里写图片描述
BN：批量归一化，往batch方向做归一化，归一化维度是[N，H，W]
LN：层次归一化，往channel方向做归一化，归一化维度为[C，H，W]
IN：实例归一化，只在一个channel内做归一化，归一化维度为[H，W]
GN：介于LN和IN之间，在channel方向分group来做归一化，归一化的维度为[C//G , H, W]