概述
LSTM缓解梯度消失的原因
本文主要是对LSTM缓解梯度消失的原因，从公式上进行推导理解。
对于LSTM的结构如下：
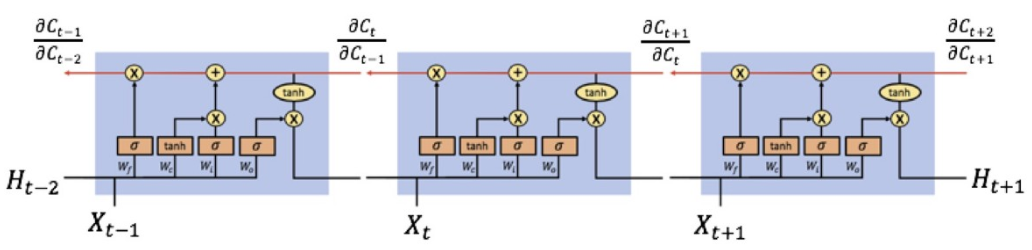
c t = c t − 1 ⊗ σ ( W f ⋅ [ H t − 1 , X t ] ) ⊕ tanh ( W c ⋅ [ H t − 1 , X t ] ) ⊗ σ ( W i ⋅ [ H t − 1 , X t ] ) c_{t}=c_{t-1} otimes sigmaleft(W_{f} cdotleft[H_{t-1}, X_{t}right]right) oplus tanh left(W_{c} cdotleft[H_{t-1}, X_{t}right]right) otimes sigmaleft(W_{i} cdotleft[H_{t-1}, X_{t}right]right) ct=ct−1⊗σ(Wf⋅[Ht−1,Xt])⊕tanh(Wc⋅[Ht−1,Xt])⊗σ(Wi⋅[Ht−1,Xt])
反向传播公式：
∂ E k ∂ W = ∂ E k ∂ H k ∂ H k ∂ C k ∂ C k ∂ C k − 1 … ∂ C 2 ∂ C 1 ∂ C 1 ∂ W = ∂ E k ∂ H k ∂ H k ∂ C k ( ∏ t = 2 k ∂ C t ∂ C t − 1 ) ∂ C 1 ∂ W begin{aligned} frac{partial E_{k}}{partial W}=& frac{partial E_{k}}{partial H_{k}} frac{partial H_{k}}{partial C_{k}} frac{partial C_{k}}{partial C_{k-1}} ldots frac{partial C_{2}}{partial C_{1}} frac{partial C_{1}}{partial W}=\ & frac{partial E_{k}}{partial H_{k}} frac{partial H_{k}}{partial C_{k}}left(prod_{t=2}^{k} frac{partial C_{t}}{partial C_{t-1}}right) frac{partial C_{1}}{partial W} end{aligned} ∂W∂Ek=∂Hk∂Ek∂Ck∂Hk∂Ck−1∂Ck…∂C1∂C2∂W∂C1=∂Hk∂Ek∂Ck∂Hk(t=2∏k∂Ct−1∂Ct)∂W∂C1
括号中的部分是累乘项：
∂ c t ∂ c t − 1 = σ ( W f ⋅ [ H t − 1 , X t ] ) + d d C t − 1 ( tanh ( W c ⋅ [ H t − 1 , X t ] ) ⊗ σ ( W i ⋅ [ H t − 1 , X t ] ) ) frac{partial c_{t}}{partial c_{t-1}}=sigmaleft(W_{f} cdotleft[H_{t-1}, X_{t}right]right) + frac{d}{d mathcal{C}_{t-1}}left(tanh left(W_{c} cdotleft[H_{t-1}, X_{t}right]right) otimes sigmaleft(W_{i} cdotleft[H_{t-1}, X_{t}right]right)right) ∂ct−1∂ct=σ(Wf⋅[Ht−1,Xt])+dCt−1d(tanh(Wc⋅[Ht−1,Xt])⊗σ(Wi⋅[Ht−1,Xt]))
也就是说，这里的累乘单元是两项和形式，其中前部分是遗忘门的值。遗忘门决定了上一个细胞状态的保留比例，其取值可以接近于1，也就是说可以把遗忘门看成： σ ( W f ⋅ [ H t − 1 , X t ] ) ≈ 1 → sigmaleft(W_{f} cdotleft[H_{t-1}, X_{t}right]right) approx overrightarrow{1} σ(Wf⋅[Ht−1,Xt])≈1，所以LSTM中：
∂ E k ∂ W ≈ ∂ E k ∂ H k ∂ H k ∂ c k ( Π t = 2 k σ ( W f ⋅ [ H t − 1 , X t ] ) ) ∂ C 1 ∂ w ↛ 0 frac{partial E_{k}}{partial W} approx frac{partial E_{k}}{partial H_{k}} frac{partial H_{k}}{partial c_{k}}left(Pi_{t=2}^{k} sigmaleft(W_{f} cdotleft[H_{t-1}, X_{t}right]right)right) frac{partial C_{1}}{partial w} nrightarrow 0 ∂W∂Ek≈∂Hk∂Ek∂ck∂Hk(Πt=2kσ(Wf⋅[Ht−1,Xt]))∂w∂C1↛0
所以，LSTM能缓解梯度消失。
最后
以上就是慈祥小鸽子为你收集整理的LSTM缓解梯度消失的原因的全部内容，希望文章能够帮你解决LSTM缓解梯度消失的原因所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复