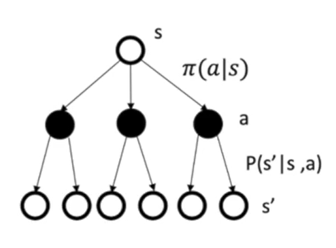
由图(1),在马尔科夫决策过程中:

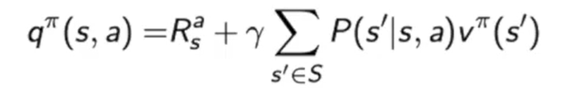
由公式(1)和公式(2),可以简写成v(s) = E[q(s, a)],q(s, a) = E[r + v(s’)],合并得到v(s) = E[r + v(s’)]和q(s, a) = E[r + E[q(s’, a’)]], 即q值的更新是根据下个状态q值的均值来更新的,并不是通过下个状态最大的q值来更新的。
再来看Q-Learning更新Q值的公式:
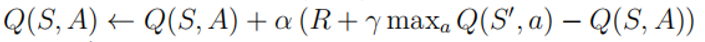
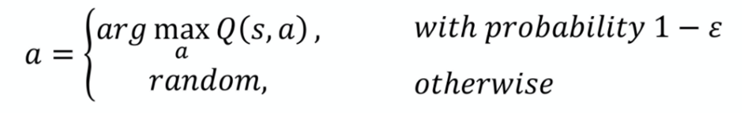
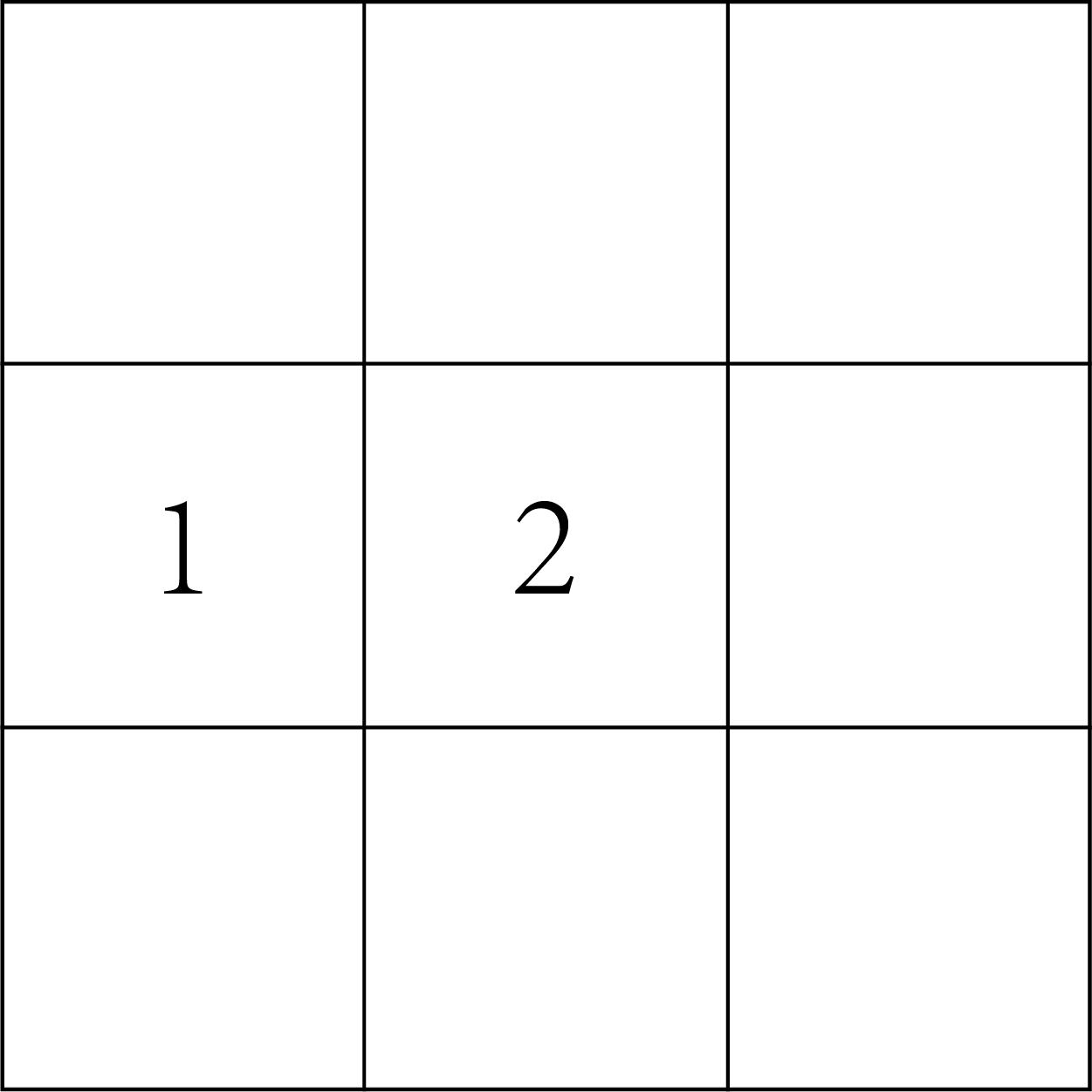
对于一个3x3大小的地图,Q表格的维度是9x4,即9个状态,每个状态又有4个Q值,共36个Q值。Q-Learning算法的过程即不断更新Q表格中的Q值。
由上述公式(3)可知,假设从方格1向右走一步到达方格2,则可以写成:
Q(1, 右) <- Q(1, 右) + α(R(1, 右) + γmaxQ(2, a))
其中maxQ(2, a)就是在Q(2, 上)、Q(2, 下)、Q(2, 左)、Q(2, 右)4个值中选一个最大的。这就出现了问题,因为Q(2, 上)、Q(2, 下)、Q(2, 左)、Q(2, 右)中的每个值也是通过公式(3)更新得到的,也就是说每个值都被过估计了。
如果这4个值被过估计了相同的幅度,即过估计量是均匀的,这样的话从4个值中选出的值函数还是最大的值函数,在通过公式(4)用贪心策略选取方格2这一状态的最优动作没有影响,并且对更新Q(1, 右)没有影响。但是,在实际情况下,过估计量并不是均匀的,从而导致从4个值中选出的值函数不一定是最大的值函数,导致在通过公式(4)用贪心策略选取方格2这一状态的最优动作非优,并且影响了Q(1, 右)的更新。
以上仅为个人理解,若发现有不对的地方欢迎大家批评指正。
最后
以上就是微笑纸飞机最近收集整理的关于Q-Learning中的Q值为何会被过估计?(即Double-DQN解决了什么问题)的全部内容,更多相关Q-Learning中内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复