Verilog语言生成4位伪随机码

78 阅读 0 评论 52 点赞

我是靠谱客的博主孤独帅哥，最近开发中收集的这篇文章主要介绍Verilog语言生成4位伪随机码，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Verilog语言生成4位伪随机码

- 关于伪随机码的定义及基本特性
- 本原多项式
- 代码

关于伪随机码的定义及基本特性

伪随机码又称伪随机序列，它是具有类似于随机序列基本特性的确定序列。通常广泛应用二进制序列，因此我们仅限于研究二进制序列。二进制独立随机序列在概率论中一般称为贝努利(Bernoulli)序列，它由两个元素(符号)0, 1或1, -1组成。序列中不同位置的元素取值相互独立取0取1的概率相等等于1/2：我们简称此种系列为随机系列。

随机序列具有以下三个基本特性：

1)在序列中“0”和“1”出现的相对频率各为1/2。

2)序列中连0或连1称为游程连0或连1的个数称为游程的长度，序列中长度为1的游程数占游程总数的1/2；长度为2的游程数占游程总数的1/4；长度为3的游程数占游程总数的1/8；长度为n的游程数占游程总数的1/2n(对于所有有限的n)。此性质我们简称为随机序列的游程特性。

3)如果将给定的随机序列位移任何个元素，则所得序列的和原序列的对应的元素有一半相同，一半不同。

如果确定序列近似满足以上三个特性则称此确定序列为伪随机序列。
————————————————
原文链接：https://blog.csdn.net/qq_40532956/article/details/80109534

本原多项式

在设计伪随机码前要确定码长，从而确定本原多项式，常用的本原多项式见下表所示：
常用本原多项式
m序列周期为2ⁿ-1，由移位寄存器和异或门构成，n表示移位寄存器的个数。

另外，在查阅资料的过程中还了解到移位寄存器的相关知识，可以参考如下的博客：
https://blog.csdn.net/qq_23947237/article/details/90238787

其中对于伪随机码、m序列、移位寄存器和仿真内容进行了较为详细的梳理和总结。

代码

Verilog语言和通信相关的伪随机码知识都是笔者第一次接触，在长时间的查阅相关资料学习基础知识和应用方法后决定首先选择码长为4的编码进行练习。

m序列是最常用的伪随机序列，是最长线性反馈移位寄存器序列的简称。如果是4级的寄存器（下面都假设n=4），那么最长周期是2⁴-1=15。

m序列的特征多项式必须是4次的本原多项式。必须满足条件：

1、既约的；

2、可整除x¹⁵+1，这里15=2⁴-1；

3、不可整除x^q+1，q<15。

由上表，已知4次的本原多项式为x^4+x+1，那么反馈逻辑就是a4 = a1 + a0（mod 2）。

然后赋予初状态为0001，那么由线性反馈逻辑和初状态就能决定m序列了。

编译环境：QuartusII 15.0
仿真环境：Modelsim Altera 10.3d（与Quartus15.0适配版）

module testcode(clk,rst_n,out_data);
input clk;
input rst_n;
output reg out_data; //输出的伪随机码
reg [3:0]temp = 4’b0001;
always @(posedge clk or negedge rst_n)
begin
if(!rst_n) //复位信号无效时
out_data <= 1’b0;
else begin
temp[0] <= temp[2] + temp[3]; //t0=t2+t3
temp[3:1] <= temp[2:0]; //t3-1=t2-0,即右移一位
out_data <= temp[3]; //输出数据为t3
end
end
endmodule

仿真程序：

`timescale 1ns/1ns
module testcode_tb;
reg clk,rst_n;
wire out_data;
testcode testcode_0(.clk(clk),
.rst_n(rst_n),
.out_data(out_data));
initial clk = 1;
always #25 clk = ~clk;
initial begin
rst_n <= 1’b0;
#200;
rst_n <= 1’b1;
#5000;
$stop;
end

仿真效果：

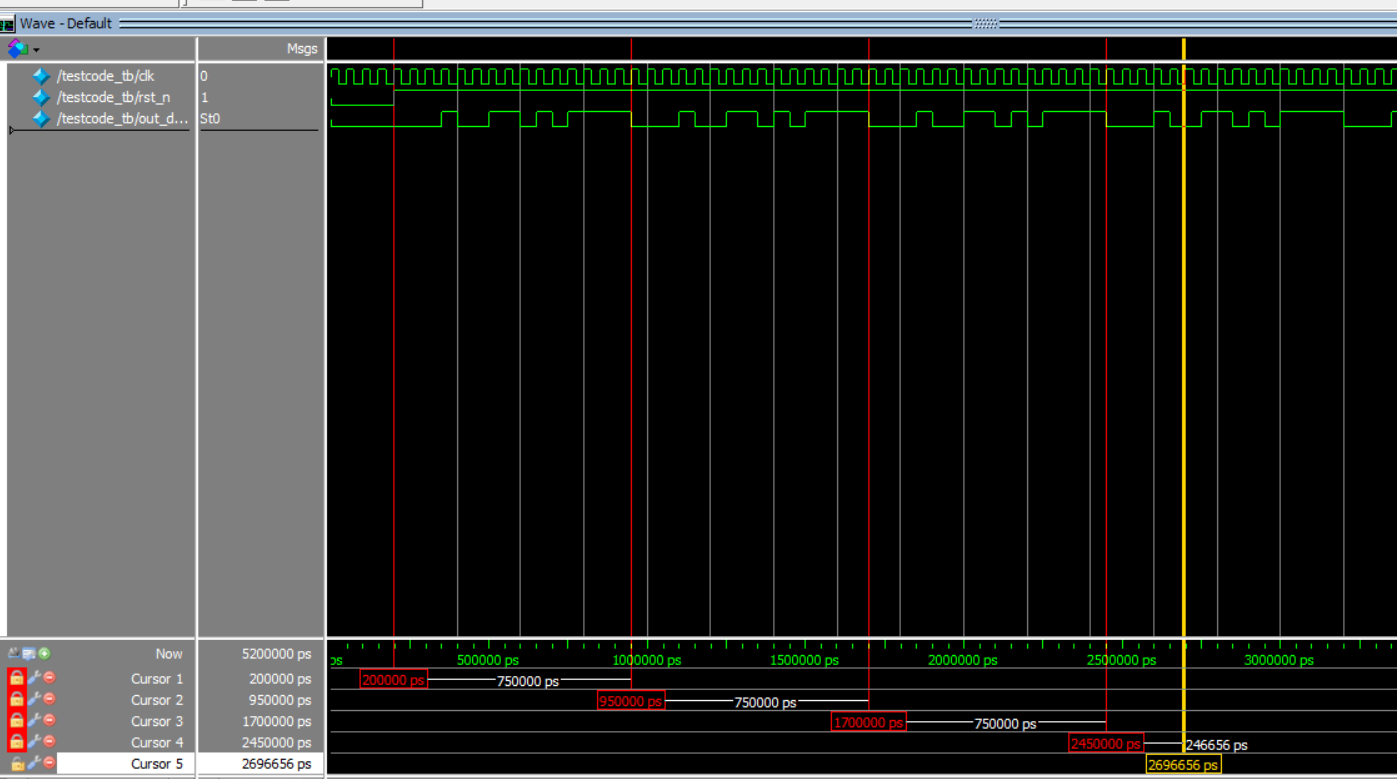
在这里插入图片描述
从仿真效果来看，基本实现了预计的效果。