matlab 正态分布

正态分布（Normal distribution）又名高斯分布（Gaussian distribution）

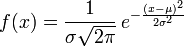
function [P,V] = initializeProbability(P0,sigma)

V = ( (P0-6*sigma):0.01:(P0+6*sigma) )';% or set themself

% normal distribution centered around P0
nd = (1/(sigma*sqrt(2*pi)))*exp(-(V-P0).^2/(2*sigma^2));
nd = nd/sum(nd);  %归一化y轴为<1
P = nd;

正态分布的一些性质:

1. 如果且a与b是实数，那么aX + b∼N(aμ + b,(aσ)²) (参见期望值和方差).
2. 如果与是统计独立的正态随机变量，那么:
   • 它们的和也满足正态分布 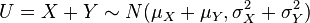(proof).
   • 它们的差也满足正态分布.
   • U与V两者是相互独立的。
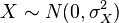3. 如果和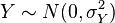是独立正态随机变量，那么:
   • 它们的积XY服从概率密度函数为p的分布

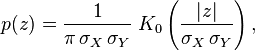     其中 K ₀是贝塞尔函数（modified Bessel function）

   • 它们的比符合柯西分布，满足X / Y∼Cauchy(0,σ_X / σ_Y).
4. 如果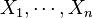为独立标准正态随机变量，那么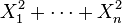服从自由度为n的卡方分布。

• 参数为n和p的二项分布，在n相当大而且p不接近1或者0时近似于正态分布（有的参考书建议仅在np与n(1 − p)至少为5时才能使用这一近似）。

近似正态分布平均数为μ = np且方差为σ² = np(1 − p).

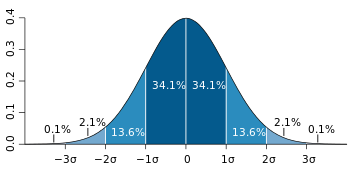
在实际应用上，常考虑一组数据具有近似于正态分布的概率分布。若其假设正确，则约68%数值分布在距离平均值有1个标准差之内的范围，约95%数值分布在距离平均值有2个标准差之内的范围，以及约99.7%数值分布在距离平均值有3个标准差之内的范围。称为"68-95-99.7法则"或"经验法则".

最后

以上就是老实星星为你收集整理的matlab 正态分布的全部内容，希望文章能够帮你解决matlab 正态分布所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。