一、 冗余机械臂基本概念与典型结构

1.1 冗余机械臂基本概念

  要研究冗余机械臂，就首先要了解什么是冗余机械臂？有什么用？下面给出相关参考资料中关于冗余机械臂的定义，参考文献可见文末
  冗余机械臂定义：假设机器人操作臂关节空间的维数为n，操作空间的维数为m，当n>m时，该机械臂即为冗余机械臂。
  冗余机械臂的优势：冗余机械臂可以增加机械臂的操作灵活性、优化关节力矩、避障碍等。

1.2 冗余机械臂典型结构

  典型的冗余机械臂如：KUKA公司的iiwa机械臂是经典的七自由度冗余机械臂，其具体结构如下图。


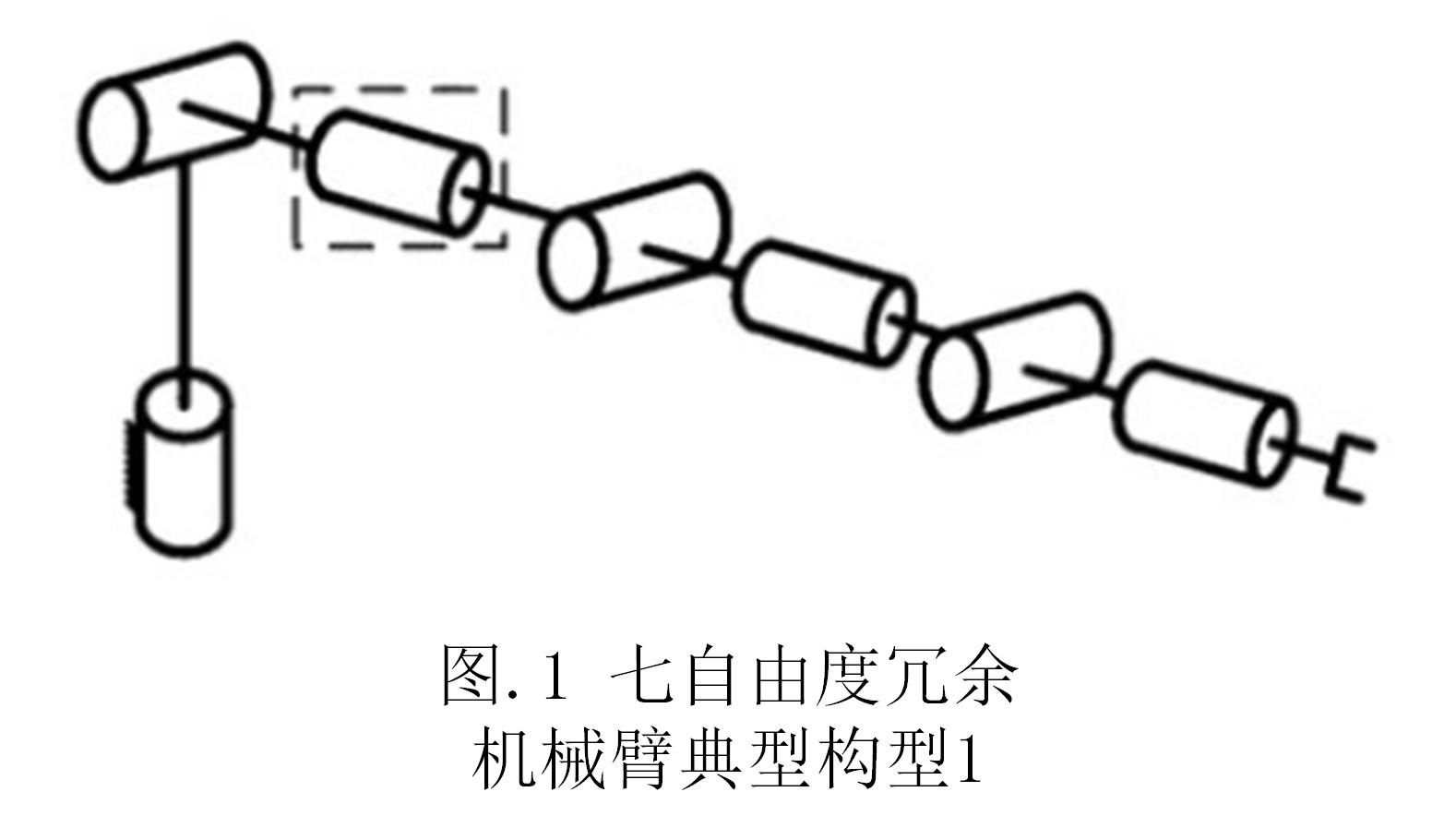
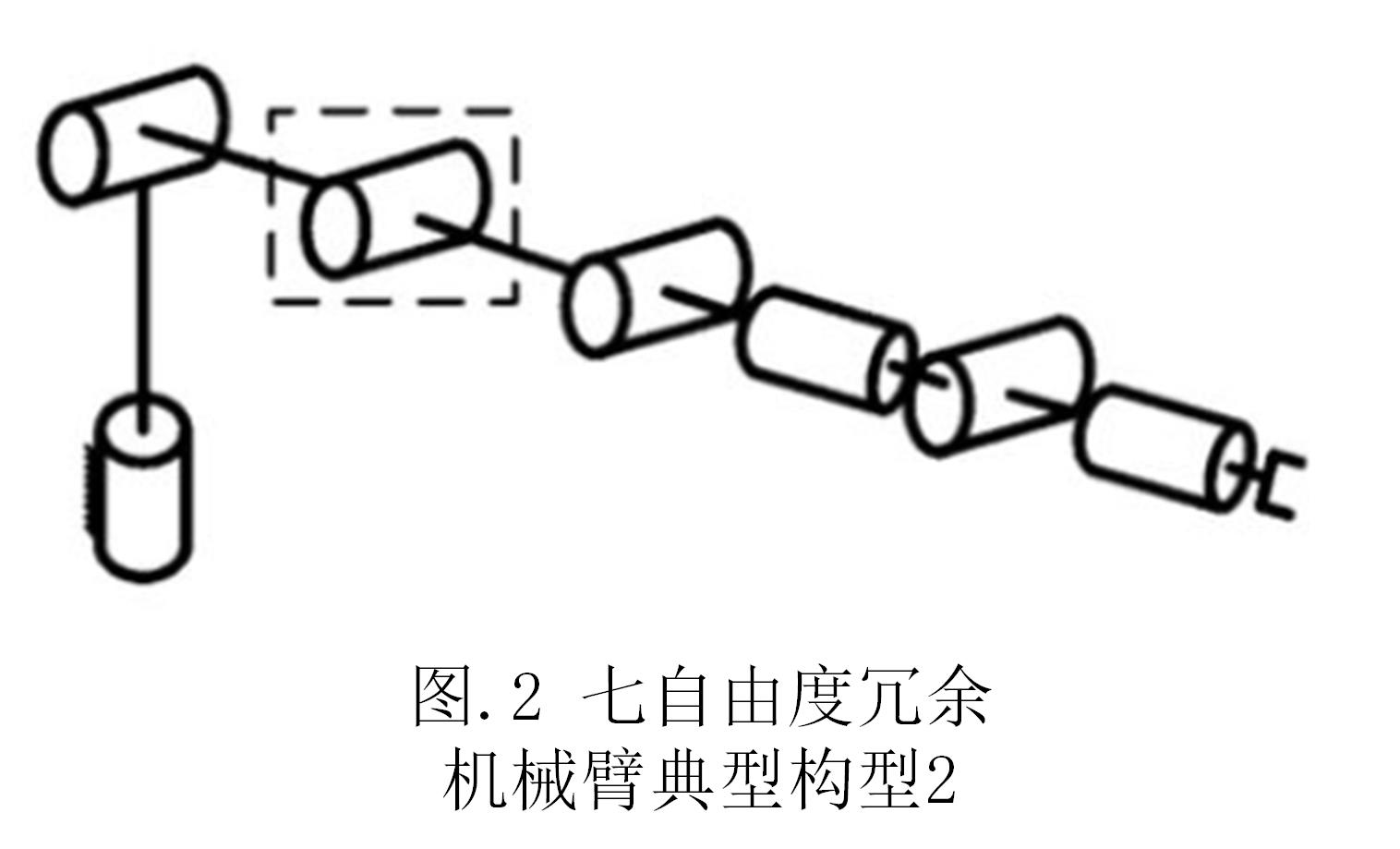
  本文主要针对构型1的七自由度冗余机械臂进行研究。

二、基于臂型角参数化解析逆运动学求解

  冗余机器人运动学逆解的主要难点是由于其冗余的特点，所以其运动学方程有无穷多组解，如何结合实际应用任务来得到合适的解是十分重要的。在进行运动学逆解分析中，只有搞清楚了困难的原因，才能找出对应的解决办法。既然冗余机器人难点在于解的无穷多，即由于自由度数与关节数的不对等造成的，那么如果能构造出自由度数与关节数相当的情况，是不是就变成了非冗余机械臂呢？基于此思想，常用的冗余机械臂解析逆解法被提出。主要有以下两种。
  基于关节角参数化解析法：其主要思想是通过人为减小待求关节角度，从而相当于减少关节待求数，这样就可以使得关节数等于操作空间数。通俗一点就是，原本待求的有七个量，现在认为的设定某个关节的角度，这样就相当于变成了六自由度机械臂运动学逆解问题。
  基于臂型角参数化解析法：既然可以人为减少关节待求数(即减小n)来达到消除冗余的效果，那也通过增加操作空间数目(即增加m)来达到消除冗余的效果，所以研究人员提出了一种基于臂型角参数化的解析法，通过臂型角来描述冗余机械臂的冗余性，通俗点将就是把冗余机械臂的冗余从某种程度来说也看作一个描述机械臂的自由度。而且，这个臂型角是可以结合实际应用场景来人为给定的。

2.1 基于臂型角参数化的冗余参数描述

  臂型机械臂运动特点：如图2.1所示，冗余机械臂在运动时，同时存在一个零空间自运动，该运动并不影响末端工具的运动。而描述这个自运动的参数就是臂型角，如下图∠E₁FE₀为臂型角。

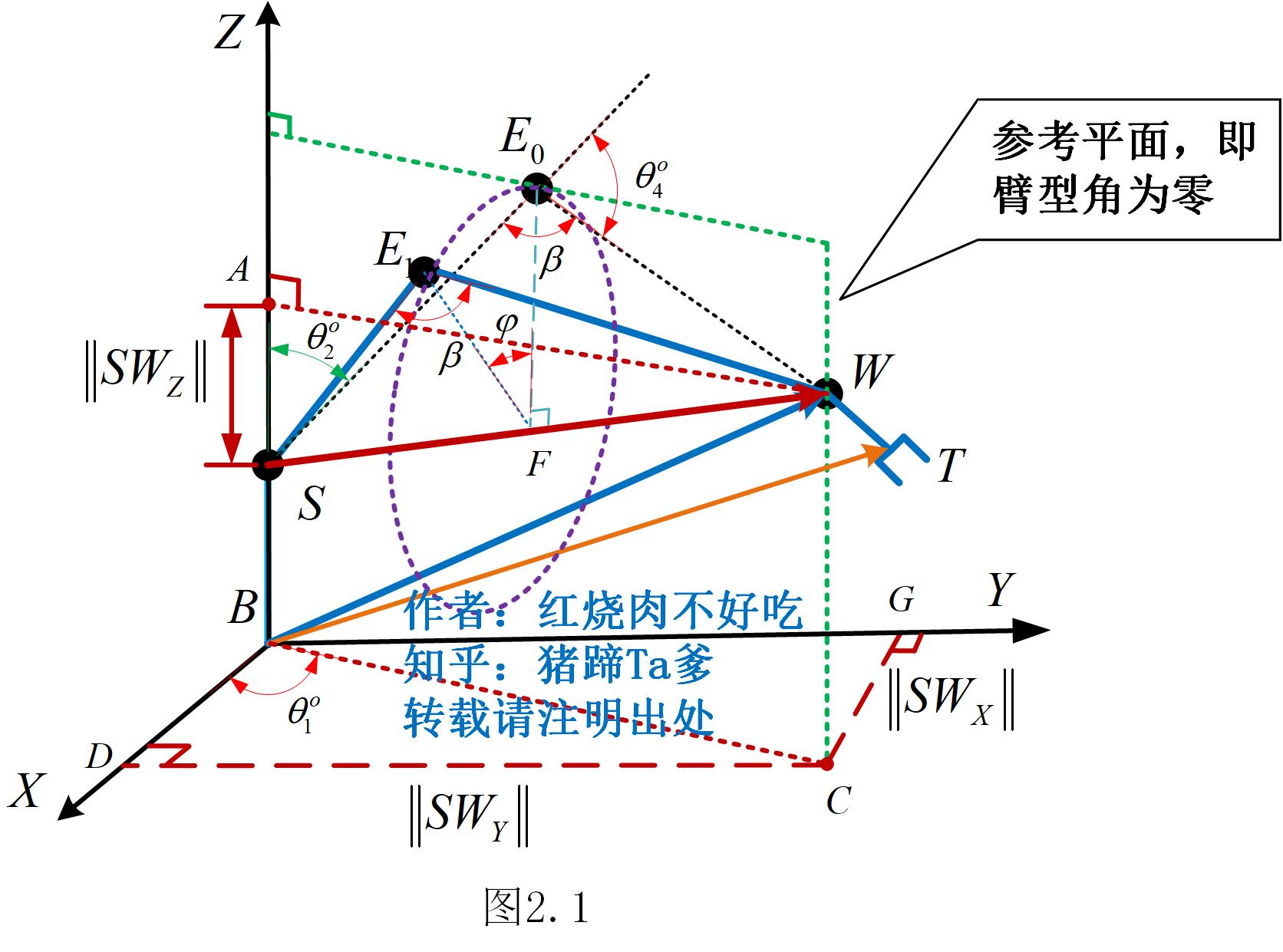
  从上图可以看出，引入臂型角来描述冗余机械臂的冗余度后，肘关节E的运动轨迹为一个圆，即图2.1中紫色虚线代表。

2.2 肘部关节角求解

  由图2.1可以看出，肘关节的角度与臂型角无关，只跟线段SE,EW,SW的长度有关。在三角形SEW中，根据余弦定理，可知：

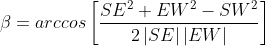
  根据肘关节处转角的描述可知，关节四的角度为：

其中正负号分别表示肘关节在上或者在下两种结构。

2.3 参考平面姿态矩阵求解

2.3.1 参考平面的定义与求解其姿态矩阵的原因

  参考平面：向量BS与SW所决定的平面。
  在进行参考平面姿态矩阵求解前，首先需要搞清楚一个问题，为什么需要求解参考平面下的姿态矩阵？作者在查阅相关文献和书籍的时候，这部分的原因都没有进行解释，可能觉得是基础常识，所以就没有说明。由此造成作者在进行该方法的学习时，不得要领，花费了大量不必要的时间。此处，为了让大家更加清楚的理解基于臂型角参数化的冗余机械臂运动学逆解的核心，进一步帮助大家节约时间，作者将针对这一部分，结合自己的理解来进行阐述，不足之处敬请指正。
  在很多参考文献中可以看到，在进行七自由度冗余机械臂运动学逆解时，参考平面的求取十分重要，它直接关系到除关节四之外的其余六个关节角的求解。相关的文献作者会在文末给出，需要的可以进一步查阅。从相关论文中可以看出，参考平面处的姿态矩阵往往与关节1到3，和关节5到7的旋转矩阵有关。为什么呢？此处就需要引入罗德里格斯旋转公式来进行解释了。罗德里格斯旋转公式的具体推导可见相关博客，此处不进一步证明。作者只说明其在冗余机械臂运动学逆解时的作用。罗德里格斯旋转公式的一大作用就是已知某向量绕某轴进行转动，则可以根据罗德里格斯旋转公式求得旋转后的向量在坐标系中的位置，其作用可推广到矩阵。从图2.1中可以看出，参考平面是绕向量SW进行旋转的，如果知道了参考平面的姿态，在指定一个臂型角之后，就可以求解出参考平面的姿态矩阵绕SW转动臂型角大小后的姿态矩阵R03。利用该矩阵，可以实现对冗余机械臂的运动学逆解。
  罗德里格斯旋转公式的证明过程可见：罗德里格斯旋转方程推导

2.3.1 参考平面姿态矩阵求解原理

  参考平面的求取是整个逆解过程中最为核心的环节，因为其直接关系到后面关节1致3，关节5致7的求解。
  根据上文给出的参考平面的几何关系，本节不加证明的给出参考平面下对应的前三个关节角的求解：





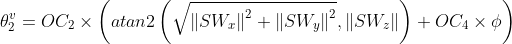
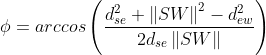
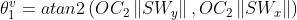
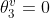
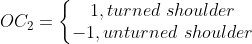
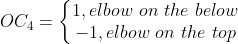
  根据关节四的大小不受臂型角影响的原理，可知在参考平面时关节四的角度与前文相等，基于此，给出参考平面时的姿态矩阵计算公式如下：

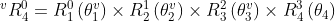
  求出了参考平面的姿态矩阵后，利用罗德里格斯旋转公式，可以得到在指定臂型角下实际位置的姿态矩阵，其计算公式如下：

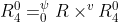
其中：罗德里格斯旋转公式如下：

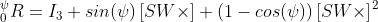
2.4 肩部关节角求解

2.5 腕部关节角求解

2.6 求解流程

三、冗余机械臂奇异性分析与关节极限位置避免

3.1 冗余机械臂奇异性分析

3.2 关节极限位置下的可行解

最后

以上就是愉快口红为你收集整理的七自由度冗余机械臂运动学逆解与工作空间分析MATLAB实现一、 冗余机械臂基本概念与典型结构二、基于臂型角参数化解析逆运动学求解三、冗余机械臂奇异性分析与关节极限位置避免的全部内容，希望文章能够帮你解决七自由度冗余机械臂运动学逆解与工作空间分析MATLAB实现一、 冗余机械臂基本概念与典型结构二、基于臂型角参数化解析逆运动学求解三、冗余机械臂奇异性分析与关节极限位置避免所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。