机械臂——六轴机械臂逆解

95 阅读 0 评论 63 点赞

我是靠谱客的博主风中冰淇淋，最近开发中收集的这篇文章主要介绍机械臂——六轴机械臂逆解，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

环境：MATLAB 2017B+Robotics Toolbox 9.10.0

前期准备：完成机械臂数学模型的建立+计算机械臂工作空间

https://blog.csdn.net/Kalenee/article/details/81990130

注意：这里采用几何法计算机械臂逆解，因此不一定适用于其他六轴机械臂构型。

一、运动学分析

连杆变换是机器人进行运动学分析的基础，其建立主要涉及到坐标变换，其中包括坐标旋转和坐标平移。

坐标旋转变换为绕坐标系的X、Y和Z轴的旋转变换，一般情况下一个旋转变换为几个基本旋转变换的合成。下面式1为绕X轴旋转的基本旋转矩阵，式2为绕Y轴旋转的基本旋转矩阵，式3为绕Z轴旋转的基本旋转矩阵。

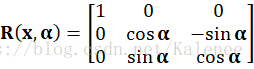
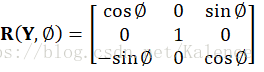
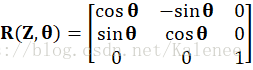
坐标平移变换为坐标系沿坐标轴X、Y和Z轴进行平移转换，平移转换后的两个坐标系的原点不同，但坐标轴相对平行。式3-4为基本平移矩阵， $p_x$ 、 $p_y$ 和 $p_z$ 为平移后的矩阵相对于原矩阵平移的距离。

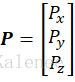
为在进行运动学分析过程中，简化计算，一般将坐标转换矩阵进行齐次变换，转变为齐次变换矩阵。

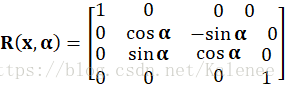
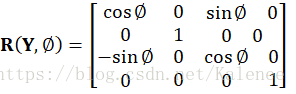
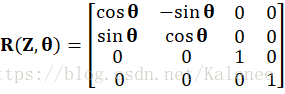
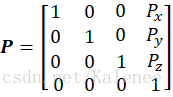
通常情况下所有的连杆变换都可以通过坐标旋转和坐标平移获得，即可通过坐标旋转变换和坐标平移变换的复合变换获得连杆变换矩阵。如图1为两个坐标系的变换，其变换公式为下式

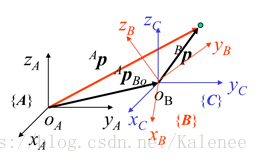
图1 旋转和平移复合的一般坐标变换

根据前面博文建立的机械臂数学模型，按照各关节坐标系的旋转和平移分别建立对应的齐次连杆变换矩阵：

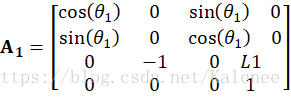
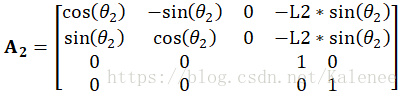
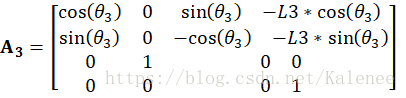
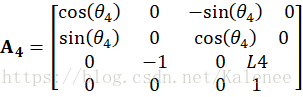
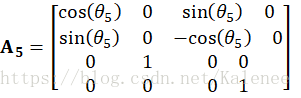
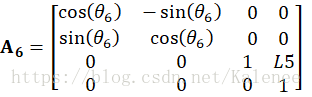
根据各关节的齐次变换矩阵可计算机器人的位置方程，通过位置方程可以获取关节变量对机械臂末端姿态的影响。在本课题中，将矩阵 $A_1$ 到 $A_6$ 按顺序进行相乘可获得设计机械臂的位置方程，同时得到机械臂末端相对于基座坐标系的位置与姿态。

关节机器人的逆运动学是根据末端位置及姿态求解机器人各关节的角度。与正运动学一组关节角度对应一个末端位姿不同，逆运动学有概率存在机器人末端的某一位姿对应多组关节角度，因此在进行求解的过程中需加入约束条件。

二、逆解计算

图2 机械臂计算逆解流程图

上图为机械臂计算逆解流程图，逆解计算首先获取需要机械臂末端执行器到达的位置的坐标及其姿态，判断其位置坐标是否在机械臂的工作空间中，如果是才开始进行逆解的计算。

然后将六个关节角度分为两组，先使用几何法计算关节角度一、二和三，因为这三个角度可在不涉及角度四、五和六的情况下进行求解。角度一主要控制机械臂整体的旋转，可投影到XOY坐标系进行计算，角度二和角度三与机械臂整体旋转无关，可投影到坐标系XOZ或者YOZ进行计算。此处单纯采用几何法完成关节角的计算，所以受机械臂构型影响较大，无法通用，对其余构型机械臂参考价值不大，因此此处不列出计算具体流程。完成角度一、二和三计算后，将其结果代入机械臂的DH矩阵中，为后续计算做准备。

接着，计算 $A_4$ 和 $A_5$ 的乘积，并在代入角度一、二和三后计算 $A^-^1_1$ 、 $A^-^1_2$ 、 $A^-^1_3$ 和 $T_5$ 的乘积，两次计算所获得的结果应该是相等的，因此，根据计算所获得的矩阵，比较两边矩阵内部的各元素，获取一边为常数，另一边为单个未知数的两个元素，通过求解该单一未知数分别求解角度四、五和六。

因所获得的解有可能并不唯一，所以最后根据约束条件，对所获得的解进行筛选，排除不在约束条件内部的解，并根据路径最短原则选取最优解作为最终的结果。

三、程序实现

%六轴机械臂几何法反解计算
%流程：输入末端点坐标，检查是否在工作空间范围内，计算反解，正解验证
clc;
clear;
format short;%保留精度

%角度转换
du=pi/180;     %度
radian=180/pi; %弧度

%% 模型导入
robot_hand;

%% 工作空间计算
figurews;

%% DH参数矩阵
R=[0;0;0];
syms theta1 theta2 theta3 theta4 theta5 theta6
%  theta    d   a      alpha
L=[0      L1   0      -pi/2 ;
   pi/2   0    -L2    0     ;
   0      0    -L3    pi/2  ;
   0      L4   0      -pi/2 ;
   pi/2   0    0      pi/2  ;    
   0      L5   0      0     ];
T_start=six_link.fkine([0 0 0 0 0 0]);
q_test=[pi/4 pi/3 pi/3 pi/6 pi/3 pi/4];
T_test_end=six_link.fkine(q_test);
  
A{1}=trotz(theta1)*transl(0,0,L(1,2))*trotx(L(1,4))*transl(L(1,3),0,0);
A{2}=trotz(theta2)*transl(0,0,L(2,2))*trotx(L(2,4))*transl(L(2,3),0,0);
A{3}=trotz(theta3)*transl(0,0,L(3,2))*trotx(L(3,4))*transl(L(3,3),0,0);
A{4}=trotz(theta4)*transl(0,0,L(4,2))*trotx(L(4,4))*transl(L(4,3),0,0);
A{5}=trotz(theta5)*transl(0,0,L(5,2))*trotx(L(5,4))*transl(L(5,3),0,0);
A{6}=trotz(theta6)*transl(0,0,L(6,2))*trotx(L(6,4))*transl(L(6,3),0,0);

 T6=A{1}*A{2}*A{3}*A{4}*A{5}*A{6};

% 输入末端点坐标, 末端姿态默认与初始状态一致
 point_xyz=inputdlg({'X','Y','Z'},'末端点坐标',1,{'52.7','0','48.75'});
 point_x=str2double(point_xyz{1});
 point_y=str2double(point_xyz{2});
 point_z=str2double(point_xyz{3});

%% target point
X=point_x;
Y=point_y;
Z=point_z;
Judge_Point_in_WS=0;

if (X<X_max)&&(X>X_min)
    if (Y<Y_max)&&(Y>Y_min)
        if (Z<Z_max)&&(Z>Z_min)
            if (X^2+Y^2+Z^2)<R_max_squre
                Judge_Point_in_WS=1;
            end
        end
    end
end

    %% ikine
if Judge_Point_in_WS==1
   T06=[T_start(1:3,1:3) [X;Y;Z];
        0    0    0  1] 
  T5=T06*inv(A{6});
  X_t=double(T5(1,4));
  Y_t=double(T5(2,4));
  Z_t=double(T5(3,4));
  %T45=A{3}*A{4};
  %double(T45(3,4));
  
  r_squre=X_t^2+Y_t^2;
  r_gen=sqrt(r_squre);
  S=Z_t-L1;
  R_squre=S^2+r_squre;
  R_gen=sqrt(R_squre);
  
  %% solve theta1
  theta11=atan2(Y_t,X_t);
  theta11=double(real(theta11));
  
  %% solve theta3
  a33=sqrt(L3^2+L4^2);
  a33_angle=atan(L4/L3);
  cos_theta3_bu=(L2^2+a33^2-R_squre)/(2*L2*a33);
  theta33=pi-acos(cos_theta3_bu)-a33_angle;
  theta33=double(theta33);

  %% solve theta2
  cos_theta2_bu=(L2^2+R_squre-a33^2)/(2*L2*R_gen);
  if S>0
     theta22=pi/2-acos(cos_theta2_bu)-atan(S/r_gen);
  else
     theta22=pi/2-acos(cos_theta2_bu)+atan(-S/r_gen);
  end
  theta22=double(theta22);
% end 
% 
  %% solve to theta4 theta5 theta6
  %% 赋值
  A11=trotz(L(1,1)+theta11)*transl(0,0,L(1,2))*trotx(L(1,4))*transl(L(1,3),0,0);
  A22=trotz(L(2,1)+theta22)*transl(0,0,L(2,2))*trotx(L(2,4))*transl(L(2,3),0,0);
  A33=trotz(L(3,1)+theta33)*transl(0,0,L(3,2))*trotx(L(3,4))*transl(L(3,3),0,0);
       
 %% solve theta4 theta5 theta6
  T321=inv(A11*A22*A33);
  T45=simplify(A{4}*A{5});
  kimejer=simplify(T321*T5);
  
      %%  solve theta6
      str_solve=kimejer(3,2);%解出theta6 的方程式,if theta6 is right, theta45 then will right
      AA=double(subs(str_solve,[cos(theta6),sin(theta6)],[1,0]));
      BB=double(subs(str_solve,[cos(theta6),sin(theta6)],[0,1]));
      theta66=atan(-AA/BB);

      %% solve theta4 and theta5
      kimejer2=simplify(subs(kimejer,theta6,theta66));
          %% solve theta4 
          theta441=double(atan(kimejer2(2,1)/kimejer2(1,1)));
          if (theta441*radian)<q4_end&&(theta441*radian)>q4_s
              theta44=theta441;
          end

          %% solve theta5
          theta551=double(atan2(-kimejer2(3,1),kimejer2(3,3))-pi/2);
          if (theta551*radian)<q5_end&&(theta551*radian)>q5_s
              theta55=theta551;
          end

  %% check
  theta_ikine=[theta11,theta22,theta33,theta44,theta55,theta66]*radian 
  T_check=six_link.fkine([theta11 theta22 theta33 theta44 theta55 theta66])
  figure (2)
  hold on 
      six_link.plot([theta11,theta22,theta33,theta44,theta55,theta66], plotopt{:});
  hold off
end

参考：

宋金华. 六轴工业机器人的轨迹规划与控制系统研究[D].哈尔滨工业大学,2013.

邢婷婷. 上下料机械手的运动学及动力学分析与仿真[D].青岛科技大学,2012.

李洪波. 冗余七自由度串并联拟人手臂的设计研究[D].河北工业大学,2003.