数模算法 — 蒙特卡罗算法及Matlab案例

53 阅读 0 评论 35 点赞

我是靠谱客的博主欣慰毛巾，最近开发中收集的这篇文章主要介绍数模算法 — 蒙特卡罗算法及Matlab案例，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

本文为博主编写文章，未经博主允许转载，转载请注明出处：https://blog.csdn.net/weixin_42604241/article/details/97382158

蒙特卡罗算法（方法）定义

蒙特卡罗方法又称统计模拟法、随机抽样技术，是一种概率算法（随机模拟方法），以概率和统计理论方法为基础的一种计算方法，是使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。为象征性地表明这一方法的概率统计特征，故借用赌城蒙特卡罗命名。

该方法在金融工程学，宏观经济学，计算物理学（如粒子输运计算、量子热力学计算、空气动力学计算）等领域应用广泛。

 蒙特卡罗算法：采样越多，越近似最优解；
 拉斯维加斯算法：采样越多，越有机会找到最优解。

举个例子，假如筐里有100个苹果，让我每次闭眼拿1个，挑出最大的。于是我随机拿1个，再随机拿1个跟它比，留下大的，再随机拿1个……我每拿一次，留下的苹果都至少不比上次的小。拿的次数越多，挑出的苹果就越大，但我除非拿100次，否则无法肯定挑出了最大的。这个挑苹果的算法，就属于蒙特卡罗算法——尽量找好的，但不保证是最好的。
而拉斯维加斯算法，则是另一种情况。假如有一把锁，给我100把钥匙，只有1把是对的。于是我每次随机拿1把钥匙去试，打不开就再换1把。我试的次数越多，打开（最优解）的机会就越大，但在打开之前，那些错的钥匙都是没有用的。这个试钥匙的算法，就是拉斯维加斯算法——尽量找最好的，但不保证能找到。
所以你看，这两个词并不深奥，它只是概括了随机算法的特性，算法本身可能复杂，也可能简单。这两个词本身是两座著名赌城，因为赌博中体现了许多随机算法，所以借过来命名。这两类随机算法之间的选择，往往受到问题的局限。如果问题要求在有限采样内，必须给出一个解，但不要求是最优解，那就要用蒙特卡罗算法。反之，如果问题要求必须给出最优解，但对采样没有限制，那就要用拉斯维加斯算法。

如下图，例如我们想要计算二维空间的阴影图形的面积，就可以使用蒙特卡罗算法。
我们在x属于[0,2]，y属于[0,4]之间，任取1000个随机点，结果如下：

我们计算落在图中阴影图形中的点（其y<=x^2）的个数与1000做比，这个值就近似认为是图形与[0,2]和[0,4]围成矩形的面积的比，矩形的面积为8是已知，可以用刚才算的比值乘以8就得到图中图形的近似解。
蒙特卡罗算法思想就是上述例子使用的想法，上述问题可以直接通过积分求得，但一些现实问题，比如我们玩过的用圈套娃娃游戏，为什么套种我们想要的娃娃这么难呢？这个问题就不能直接用积分求解，因为里面有圈的半径和娃娃的半径，此时我们可以通过蒙特卡罗算法进行模拟。

蒙特卡罗算法案例Matlab求解:

【例】用蒙特卡洛模拟法求圆周率PI（希腊字母 π：实际上约等于3.141592654）
如图，红色线条为平面上圆心在原点的单位圆，圆的面积为PI，黑色线条构成边长为2的正方形。
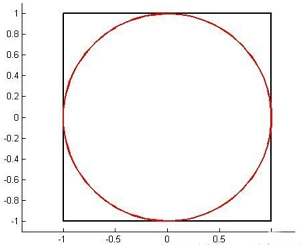
在这里插入图片描述
设相互独立的随机变量x,y均服从[-1,1]上的均匀分布，则(x，y)服从{-1≤x≤1, -1≤y≤1}上的二元均匀分布（即图中正方形区域上的二元均匀分布），记作：事件A = {x^2 + y^2 ≤ 1}，则事件A发生的概率等于单位圆面积除以边长为2的正方形的面积，即P(A) = PI/4。
可得圆周率PI = 4P(A)。而P(A)可以通过蒙特卡洛模拟法求得，在图1中正方形内随机投点（即横坐标X和纵坐标Y都是[-1,1]上均匀分布的随机数），落在单位圆内的点的个数m与点的总数n的比值m/n可以作为A事件的概率P(A)的近似，随着投点总数的增加，m/n会越来越接近于P(A)，从而可以得到逐渐接近于PI的模拟值。

MATLAB代码：

%P(A) = PI/4 => 圆周率PI = 4P(A)
%总的实验次数  
n = input('请输入实验次数 n:');  
%落在圆中点的次数 
m = 0;  
%循环实验  
for i = 1:n  
    x = 2 * rand-1;  %产生-1至1的随机数
    if (x^2 + y^2 <= 1) 
        m = m + 1;  
    end  
end  
%显示结果  
pa=m/n;     %事件A的概率
PI=4*pa;    %计算得到的圆周率
fprintf('事件A的概率pa=%dn',pa);
fprintf('计算得到的圆周率PI = %dn',PI); 

%X = rand 返回一个在区间 (0,1) 内均匀分布的随机数。
%随机数是由随机种子根据一定的计算方法计算出来的数值。
%所以，只要计算方法一定，随机种子一定，那么产生的随机数就不会变。

运行结果：
在这里插入图片描述
可得：
实验次数 n:10000000000
事件A的概率pa=7.853945e-01
计算得到的圆周率PI = 3.141578e+00（约等于3.141592654）

命令行窗口运行结果：

PI_test
请输入实验次数 n:10000
事件A的概率pa=7.855000e-01
计算得到的圆周率PI = 3.142000e+00

PI_test
请输入实验次数 n:100000
事件A的概率pa=7.850300e-01
计算得到的圆周率PI = 3.140120e+00

PI_test
请输入实验次数 n:1000000
事件A的概率pa=7.854980e-01
计算得到的圆周率PI = 3.141992e+00

PI_test
请输入实验次数 n:10000000
事件A的概率pa=7.854455e-01
计算得到的圆周率PI = 3.141782e+00

PI_test
请输入实验次数 n:100000000
事件A的概率pa=7.854134e-01
计算得到的圆周率PI = 3.141654e+00

PI_test
请输入实验次数 n:1000000000
事件A的概率pa=7.854160e-01
计算得到的圆周率PI = 3.141664e+00

PI_test
请输入实验次数 n:10000000000
事件A的概率pa=7.853945e-01
计算得到的圆周率PI = 3.141578e+00
注：最后一次的总运行时间较长，电脑配置高的话运行时间不会超过30min。