超前进位加法器

         随着操作数位数的增加，电路中进位的速度对运算时间的影响也越来越大，为了提高运算速度，需要对进位过程进行分析设计快速进位链。

1 串行进位链

        串行进位链是指并行加法器中的进位信号采用串行传递。

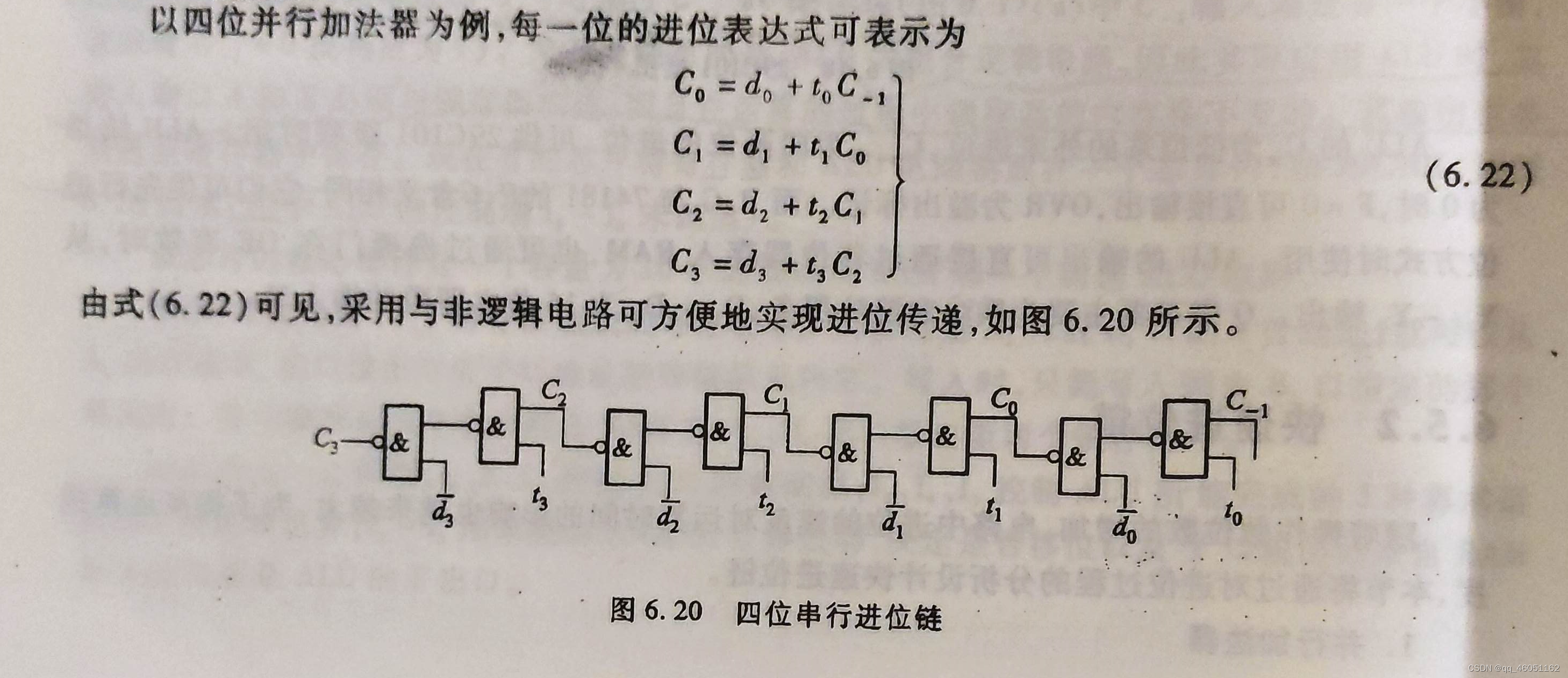
         如上图所示，给出了进位的门级传递过程。假设本地仅为di和传递进位ti都已经产生，且假设与非门的门级延迟为ty，那么每增加一位全加器，进位时间就会增加2ty。n位全加器的最长进位时间为2nty。为了解决这种时间代价线性增加的缺点，设计了并行进位链。

2 并行进位链

        并行进位链是指并行加法器中的进位信号是同时产生的，又称为先行进位、跳跃进位等。理想的并行进位链是n位全加器同时产生，但实际实现有困难。通常并行进位链有单重分组和双重分组两种实现方案。

 先以简单的为例进行分析，以四位并行加法器为例

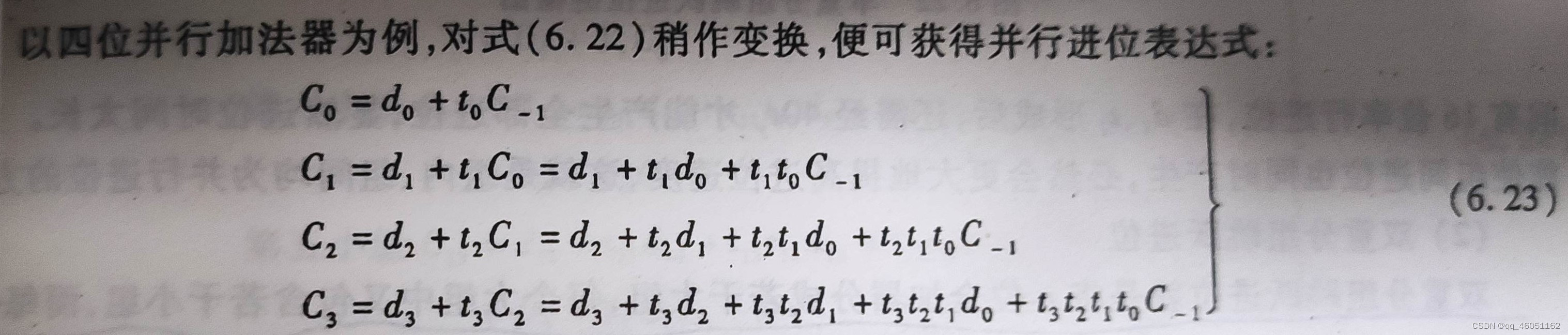
 可以发现组内的进位只与该组的C-1以及组内的一些本地进位和进位传递条件有关系。假设所有di和ti都已经产生，假设与或非门延时为1.5ty，与非门延迟为ty，那么小组的所有进位在经过2.5ty就可以全部产生。那么将这种进位链按小组串联，就可以实现更多位数的加法。以64位加法为例，采用16个这样的进位链串联，在经过40ty后就产生了所有进位。这个时间依然有点长，需要想办法改进。第一种方法是增加每个小组能够处理的位数，但这会导致整个硬件布线比较复杂，不推荐使用。第二种方法是使小组间也能够并行产生进位，这就是双重分组跳跃进位。以下图为例进行说明。

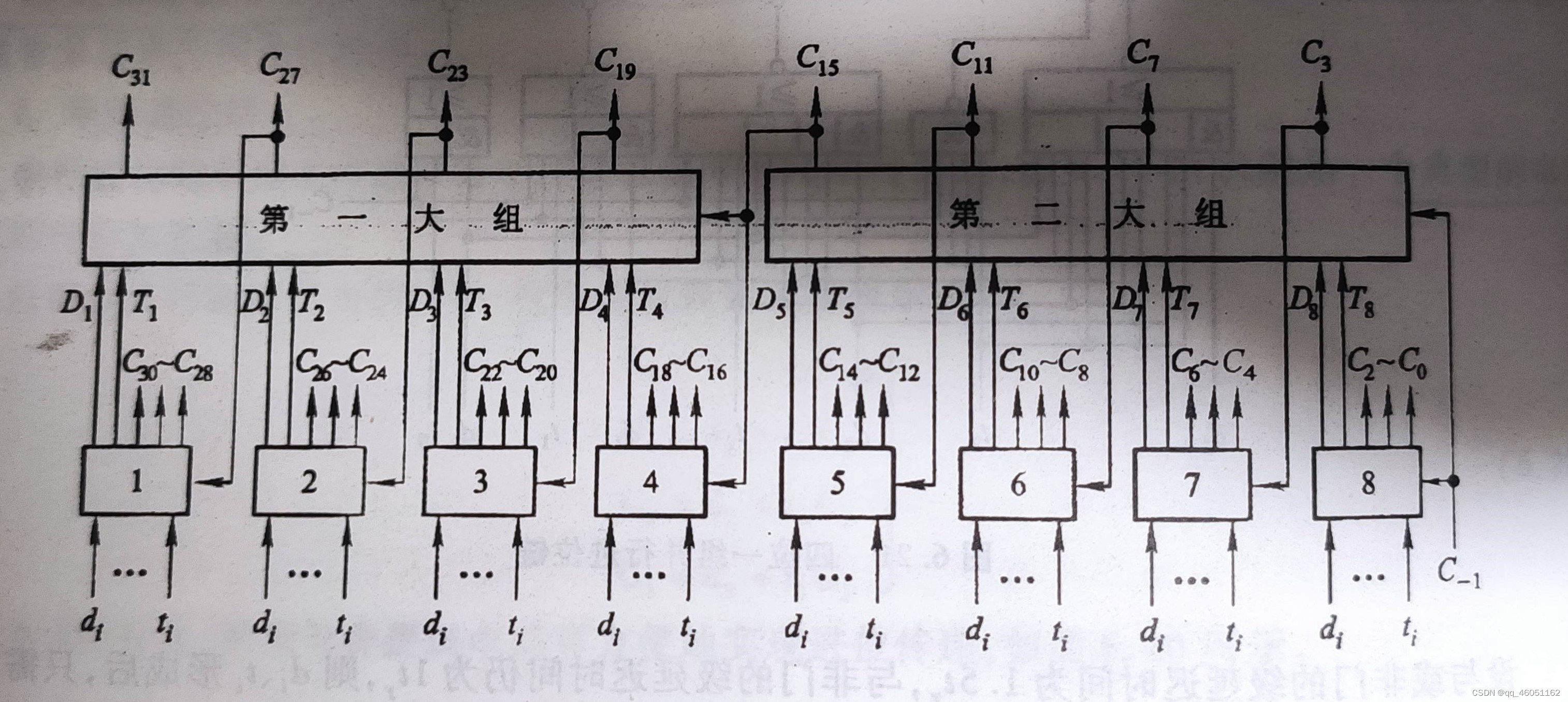
         受式6.23的影响，将每小组的最高进位进行展开。展开过程图下

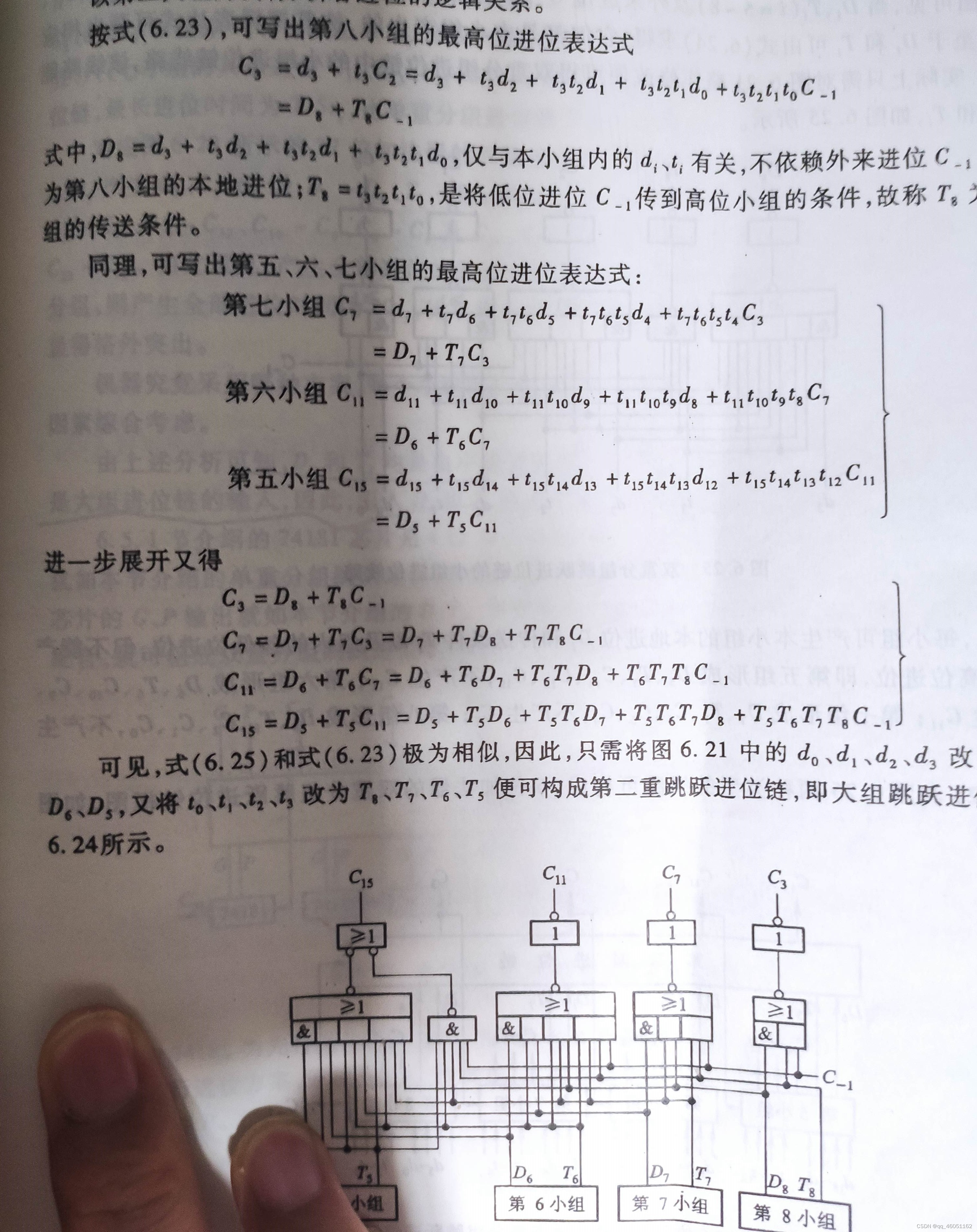
 可见，对于每个大组来说，大组中每小组的最高进位只与该组的最低进位和每小组的进位产生以及传递条件有关系，小组间没有关系，所以就可以利用这种特点来设计进位链。

下面按时间来分析每个进位的产生情况。假设所有di和ti都已经产生。

2.5ty：C2、C1、C0以及八个小组的组进位产生和传递条件。其实按照上一种方案，C3也是可以产生的，但这种方案中没有采取这种设计方法，所以此时刻没有产生。

5ty：C3、C7、C11、C15产生

7.5ty：C19、C23、C27、C31、C20、C21、C22均已产生。同时由于第二大组中每个小组的最低进位都已经产生，所以还可以形成C4、C5、C6、C8、C9、C10、C12、C13、C14均可产生。

10ty：第一大组内的所有其他进位全部产生。

所以由此可见64位加法运算时间大大减小。第一种方法的产生需要128ty，第二种方法的产生需要40ty，第三种方法的产生仅需要10ty。

个人体会： 1 把握好每个本地进位和进位传递条件的粒度。

                   2  其实这些式子的记忆也比较简单，对于某一位来说，都是改位的本地进位，以及其他地位的本地仅为是否传递到本位，传递的条件就是中间所有传递条件的与。

最后

以上就是凶狠香水为你收集整理的超前进位加法器的全部内容，希望文章能够帮你解决超前进位加法器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。