我是靠谱客的博主 标致茉莉，这篇文章主要介绍数据结构--递归遍历二叉树的c语言实现（超详细注释/实验报告）数据结构–递归遍历二叉树的c语言实现（超详细注释/实验报告），现在分享给大家，希望可以做个参考。
数据结构–递归遍历二叉树的c语言实现（超详细注释/实验报告）
知识小回顾
二叉树的遍历是指按照一定规律对二叉树中的每个结点进行访问且仅访问一次。其中的访问可知计算二叉树中结点的数据信息，打印该结点的信息们也包括对结点进行任何其他操作。
实验题目
输出二叉树的遍历结果
实验目的
- 熟悉二叉树的结点的结构
- 采用二叉链表作为存储结构建立二叉树
- 采用递归算法对其进行遍历（先序、中序、后序）
- 将遍历结果输出
实验要求
- 采用二叉链表作为存储结构建立二叉树
- 采用递归算法对其进行遍历（先序、中序、后序）
- 将遍历结果输出
实验内容和实验步骤
1.需求分析
用户输入二叉树的广义表形式，程序输出二叉树和遍历结果。
2. 概要设计
设计创建和输出二叉树的函数以及三种遍历的函数，然后再主函数中调用这几个函数来实现操作。
3. 详细设计
建立二叉树并输出二叉树的代码，之前写过了
创建并输出二叉树
下面来看看遍历的操作
因为采用了递归方法，故三种方式都差不多，只用改变一下visit的顺序即可。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33//中序遍历 void Inorder(BiTree *bt) { if(bt!=NULL) { Inorder(bt->lc); printf("%c ",bt->data); Inorder(bt->rc); } } //先序遍历 void Preorder(BiTree *bt) { if(bt!=NULL) { printf("%c ",bt->data); Preorder(bt->lc); Preorder(bt->rc); } } //后序遍历 void Postorder(BiTree *bt) { if(bt!=NULL) { Postorder(bt->lc); Postorder(bt->rc); printf("%c ",bt->data); } }
主函数部分，把程序功能打印出来，并对用户做一个引导。
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35int main()//(A(B(D,),C(,E))) (A(B(D,E),C(F,G))) ((((A),B)),(((),D),(E,F)))这个不是树 //来个波兰表达式的例子 (-(+(a,*(b,c)),/(d,e))) { BiTree *bt; char *gyb,str[MAXSIZE]; int j=1; printf("-------------------------------------------------------"); printf("n 程序功能"); printf("n 1.将按照输入的二叉广义表表示字符串 "); printf("n · 生成对应的二叉树链式结构。"); printf("n 2.输出二叉树的凹入法表示形式。"); printf("n · G--根 L--左孩子 R--右孩子"); printf("n 3.树状打印二叉树。"); printf("n · 逆时针旋转90度显示二叉树"); printf("n 4.打印出先序、中序和后续遍历的结果。"); printf("n * 输入示例：(A(B(D,),C(,E)))或(-(+(a,*(b,c)),/(d,e)))"); printf("n-------------------------------------------------------n"); printf("请输入二叉树的广义表形式：n"); gyb=str; scanf("%s",str); bt =CreatBiTreepre(gyb); printf("二叉树建立成功！n"); printf("此二叉树的凹入法表示为：n"); OutBiTree(bt); printf("树状打印二叉树：n"); PrintTree(bt,1); printf("先序遍历序列为：n"); Preorder(bt); printf("n中序遍历序列为：n"); Inorder(bt); printf("n后序遍历序列为：n"); Postorder(bt); return 0; }
4. 调试分析
遇到的问题及解决方法
- 有了前面创建和输出二叉树做铺垫，实现递归的遍历算法还是很简单的。
算法的时空分析
设二叉树有n个结点，对每个结点都要进行一次入栈和出栈的操作，即入栈和出栈各执行n次，对结点的访问也是n次。这些二叉树递归遍历算法的时间复杂度为 O ( n ) O(n) O(n)。
实验结果
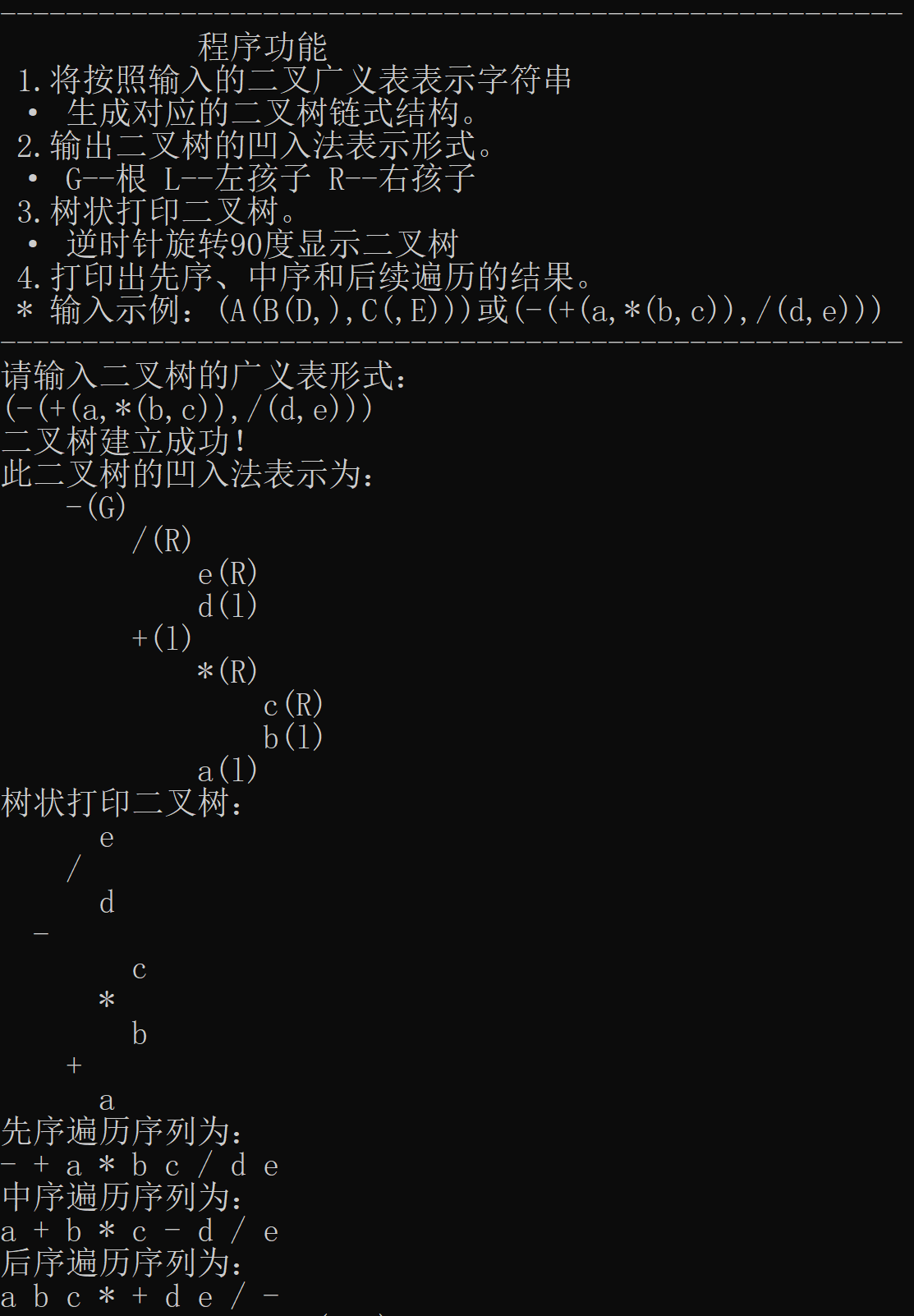
实验结果很不错，所有操作都能正常执行，用波兰表达式做例子得到了正确的输出。
这是上面分析的例子的程序给出的输出。
下面这个例子大家也可以看看。
实验总结
有了前面工作的铺垫，递归遍历就很简单了，多多重复，百炼成钢！
最后附上完整的代码
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210#include<stdio.h> #include<stdlib.h> #define MAXSIZE 255 //定义二叉树的链式存储结构，有三个域：数据域，左孩子域，右孩子域 typedef struct BiNode { char data; struct BiNode *lc; struct BiNode *rc; }BiTree; //以广义表的形式创建二叉树 BiTree *CreatBiTreepre(char *str) { BiTree *bt,*stack[MAXSIZE],*p=NULL; int top=-1,k,j=0; char ch; bt=NULL; ch=str[j]; while(ch!='') { switch(ch) { case '(': { top++; stack[top]=p; k=1; break; } case ')': { top--; break; } case ',': { k=2; break; } default: { p=(BiTree *)malloc(sizeof(BiTree)); p->data=ch; p->lc=p->rc=NULL; if(bt==NULL) { bt=p; } else { switch(k) { case 1: { stack[top]->lc=p; break; } case 2: { stack[top]->rc=p; break; } } } } } j++; ch=str[j]; } return bt;//链式存储只用知道一个，后面顺藤摸瓜就都知道了 } //采用凹入法输出二叉树 void OutBiTree(BiTree *bt) { BiTree *stack[MAXSIZE],*p; int feature[MAXSIZE][2],top,n,i,width=4; char type; if(bt!=NULL) { top=1; stack[top]=bt; feature[top][0]=width; feature[top][1]=2; while(top>0) { p=stack[top]; n=feature[top][0]; switch(feature[top][1]) { case 0: { type='l'; break; } case 1: { type='R'; break; } case 2: { type='G'; break; } } for(i=1;i<=n;i++) printf(" "); printf("%c(%c)n",p->data,type); top--; if(p->lc!=NULL) { top++; stack[top]=p->lc; feature[top][0]=n+width; feature[top][1]=0; } if(p->rc!=NULL) { top++; stack[top]=p->rc; feature[top][0]=n+width; feature[top][1]=1; } } } } void PrintTree(BiTree *bt,int nLayer) { if(bt==NULL) return ; PrintTree(bt->rc,nLayer+1); for(int i=0;i<nLayer;i++) printf(" "); printf("%cn",bt->data); PrintTree(bt->lc,nLayer+1); } //中序遍历 void Inorder(BiTree *bt) { if(bt!=NULL) { Inorder(bt->lc); printf("%c ",bt->data); Inorder(bt->rc); } } //先序遍历 void Preorder(BiTree *bt) { if(bt!=NULL) { printf("%c ",bt->data); Preorder(bt->lc); Preorder(bt->rc); } } //后序遍历 void Postorder(BiTree *bt) { if(bt!=NULL) { Postorder(bt->lc); Postorder(bt->rc); printf("%c ",bt->data); } } int main()//(A(B(D,),C(,E))) (A(B(D,E),C(F,G))) ((((A),B)),(((),D),(E,F)))这个不是树 //来个波兰表达式的例子 (-(+(a,*(b,c)),/(d,e))) { BiTree *bt; char *gyb,str[MAXSIZE]; int j=1; printf("-------------------------------------------------------"); printf("n 程序功能"); printf("n 1.将按照输入的二叉广义表表示字符串 "); printf("n · 生成对应的二叉树链式结构。"); printf("n 2.输出二叉树的凹入法表示形式。"); printf("n · G--根 L--左孩子 R--右孩子"); printf("n 3.树状打印二叉树。"); printf("n · 逆时针旋转90度显示二叉树"); printf("n 4.打印出先序、中序和后续遍历的结果。"); printf("n * 输入示例：(A(B(D,),C(,E)))或(-(+(a,*(b,c)),/(d,e)))"); printf("n-------------------------------------------------------n"); printf("请输入二叉树的广义表形式：n"); gyb=str; scanf("%s",str); bt =CreatBiTreepre(gyb); printf("二叉树建立成功！n"); printf("此二叉树的凹入法表示为：n"); OutBiTree(bt); printf("树状打印二叉树：n"); PrintTree(bt,1); printf("先序遍历序列为：n"); Preorder(bt); printf("n中序遍历序列为：n"); Inorder(bt); printf("n后序遍历序列为：n"); Postorder(bt); return 0; }
最后
以上就是标致茉莉最近收集整理的关于数据结构--递归遍历二叉树的c语言实现（超详细注释/实验报告）数据结构–递归遍历二叉树的c语言实现（超详细注释/实验报告）的全部内容，更多相关数据结构--递归遍历二叉树内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复