1.删除最大值
删除单链表中最大的元素值结点。
void DelMax(lnode *l)
{
lnode *p = l->next;
lnode *pre = l;
lnode *max = p, *maxpre = pre;
while (p)
{
if (p->data > max->data)
{
max = p;
maxpre = pre;
}
pre = p;
p = p->next;
}
maxpre->next = max->next;
delete max;
}
void main()
{
lnode *l;
l = InitList();
CreateList(l);
OutputList(l);
DelMax(l);
OutputList(l);
}
本题中需要删除最大值,故需要最大值结点及其前驱结点。因而在循环遍历中也要有前驱结点。
2.逆置链表
思路:
1.把L分为两部分:L头结点+由p指向的数据结点
2.用p遍历,利用头插法插到L。
void Reverse(lnode *l)
{
lnode *p = l->next,*q;
l->next = NULL;
while (p)
{
q = p->next;//q临时保存p之后结点
p->next = l->next;//将p插入到头结点之后
l->next = p;
p = q;
}
}
void main()
{
lnode *l = InitList();
CreateList(l);
OutputList(l);
Reverse(l);
OutputList(l);
}
3.二路并归
两个有序链表合并成一个有序链表
void Merge(lnode *a, lnode *b, lnode *&c)
{
lnode *pa = a->next, *pb = b->next;
c = a;//a的头结点用于c头结点
lnode *prec=c;//插入元素需要知道前驱结点
delete b;
while (pa&&pb)
{
if (pa->data < pb->data)
{
prec->next = pa;
prec = pa;
pa = pa->next;
}
else {
prec->next = pb;
prec = pb;
pb = pb->next;
}
}
prec->next = NULL;
if (pa)
prec->next = pa;
else
prec->next = pb;
}
void main()
{
lnode *a, *b, *c;
a = InitList();
b = InitList();//必须在这里初始化
CreateList(a);
CreateList(b);
c=InitList();
Merge(a, b, c);
OutputList(c);
}
注意:此时返回的a,b均已经作废。虽然头结点都是lnode*传递到函数中,但是由于数据结点的指针已经改变,并且都经过c头结点返回。所以,即使输出a链表,也是经过函数处理的链接方式。 为了保证不出错故而在函数删除b链表的头指针。
4.学生成绩表
其中重要的是递减排序:
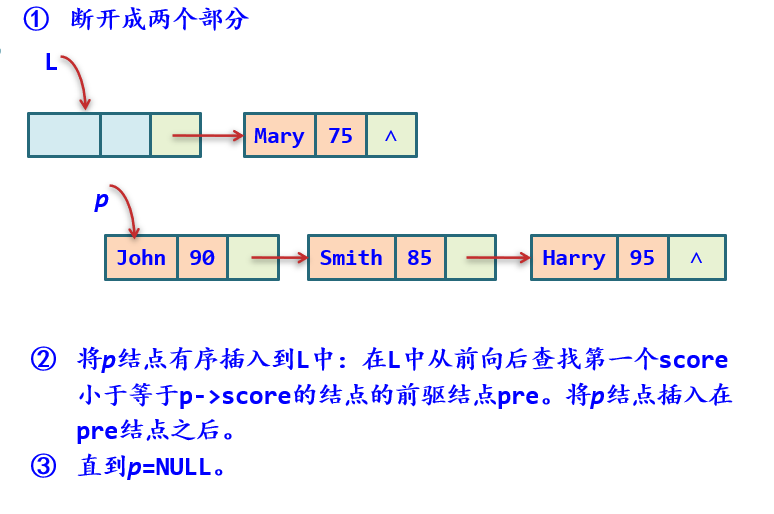
void SortList(SLink L)
{
StudList *p, *pre, *q;
p = L->next->next;
L->next->next = NULL;
while (p != NULL)
{
q = p->next;
pre = L;
while (pre->next != NULL && pre->next->score > p->score)
pre = pre->next;
p->next = pre->next;
pre->next = p;
p = q;
}
}
总代码:
#include <iostream>
#include <iomanip>
using namespace std;
typedef struct node
{
char name[10];
int score;
int Grade;
struct node *next;
}StudList, *SLink;
void DestroyList(SLink L)
{
StudList *pre = L, *p = pre->next;
while (p != NULL)
{
free(pre);
pre = p; p = p->next;
}
free(pre);
}
void DispList(SLink L)
{
StudList *p = L->next;
int i = 1;
cout << " 名次 姓 名 成绩n";
while (p != NULL)
{
cout << " " << i++ << " ";
cout << p->name;
cout << p->score;
p = p->next;
}
}
SLink CreateStudent()
{
int n, i; StudList *s, *tc;
SLink s1;
tc = (StudList *)malloc(sizeof(StudList));
s1 = tc;
cout << " 输入学生人数 : ";
cin >> n;
for (i = 0; i < n; i++)
{
s = (StudList *)malloc(sizeof(StudList));
cout << "第" << i + 1 << "个学生姓名和成绩:";
cin >> s->name;
cin >> s->score;
tc->next = s;
tc = s;
}
tc->next = NULL;
return s1;
}
void SortList(SLink L)
{
StudList *p, *pre, *q;
p = L->next->next;
L->next->next = NULL;
while (p != NULL)
{
q = p->next;
pre = L;
while (pre->next != NULL && pre->next->score > p->score)
pre = pre->next;
p->next = pre->next;
pre->next = p;
p = q;
}
}
void main()
{
SLink st;
cout << "(1)建立学生单链表n";
st = CreateStudent();
cout << "(2)按成绩递减排序n";
SortList(st);
cout << "(3)排序后的结果n"; DispList(st);
cout << "n(4)销毁学生单链表n"; DestroyList(st);
}
5.约瑟夫问题
有n个小孩围成一圈,给他们从1开始依次编号,从编号为1的小孩开始报数,数到第m个小孩出列,然后从出列的下一个小孩重新开始报数,数到第m个小孩又出列,…,如此反复直到所有的小孩全部出列为止,求整个出列序列。
如当n=6,m=5时的出列序列是5,4,6,2,3,1。
循环单链表
重点:
void Joseph(int n, int m) //求解约瑟夫序列
{
int i, j; Child *L, *p, *q;
CreateList(L, n);
for (i = 1; i <= n; i++) //出列n个小孩
{
p = L; j = 1;
while (j < m - 1) //从L结点开始报数,报到第m-1个结点
{
j++; //报数递增
p = p->next; //移到下一个结点
}
q = p->next; //q指向第m个结点
printf("%d ", q->no); //该结点出列
p->next = q->next; //删除q结点
free(q); //释放其空间
L = p->next; //从下一个结点重新开始
}
}
总代码:
#include<iostream>
#include<iomanip>
using namespace std;
typedef struct node
{
int no; //小孩编号
struct node *next; //指向下一个结点指针
} Child;
void CreateList(Child *&L, int n) //建立有n个结点的循环单链表
{
int i; Child *p, *tc; //tc指向新建循环单链表的尾结点
L = (Child *)malloc(sizeof(Child));
L->no = 1; //先建立只有一个no为1结点的单链表
tc = L;
for (i = 2; i <= n; i++)
{
p = (Child *)malloc(sizeof(Child));
p->no = i; //建立一个存放编号i的结点
tc->next = p; tc = p; //将p结点链到末尾
}
tc->next = L; //构成一个首结点为L的循环单链表
}
void Joseph(int n, int m) //求解约瑟夫序列
{
int i, j; Child *L, *p, *q;
CreateList(L, n);
for (i = 1; i <= n; i++) //出列n个小孩
{
p = L; j = 1;
while (j < m - 1) //从L结点开始报数,报到第m-1个结点
{
j++; //报数递增
p = p->next; //移到下一个结点
}
q = p->next; //q指向第m个结点
printf("%d ", q->no); //该结点出列
p->next = q->next; //删除q结点
free(q); //释放其空间
L = p->next; //从下一个结点重新开始
}
}
void main()
{
int n = 6, m = 5;
cout << n << " "<< m << "的约瑟夫序列:";
Joseph(n, m);
cout << endl;
}
最后
以上就是高高鼠标最近收集整理的关于数据结构入门系列——用链表解决实际问题(1)的全部内容,更多相关数据结构入门系列——用链表解决实际问题(1)内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复