关系代数是一种抽象的查询语言,它用对关系的运算来表达查询。
关系运算的运算对象是关系,运算结果亦是关系,关系代数的运算符包括两类:传统的集合运算和专门的关系运算两类。
传统的集合运算是从关系的水平方向,即行的角度来进行
而专门的关系代数不仅涉及行,还涉及列。

传统的集合运算
传统的集合运算是二目运算,包括并,差,交,笛卡尔积4种运算。
并(Union,表示为U):两个表或集合的联合。
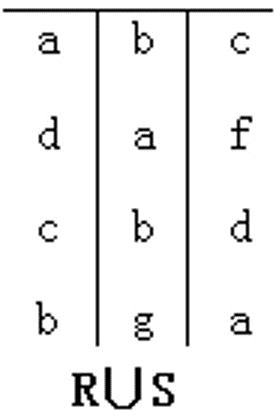
例:R1=(A,B),R2=(B,C,D)。
则R1UR2=(A,B,C,D)。
注:U集里不包含重复的属性。
差(Difference,表示位-):两个表或集合的区别。
例:R1=(A,B),R2=(B,C,D)。
则R1-R2=(A)。
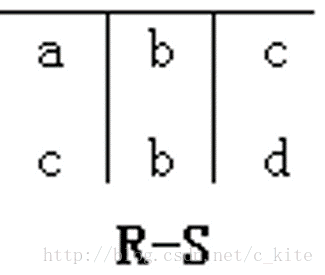
注:-集里的元素个数不能大于初始。
交(Intersection,∩):两个及以上的集合或表中具有相同属性的集合。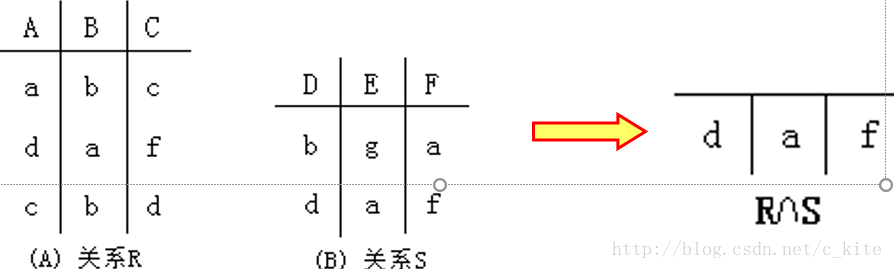
笛卡儿积(Product,表示为X):两个表或集合的组合个数。

例1:R1=(A,B),R2=(B,C,D)。
则R1xR2=(AB,AC,AD,BB,BC,BD)。
注:R1xR2集的元素个数为R1的元素个数乘R2的元素个数;
专门的关系运算
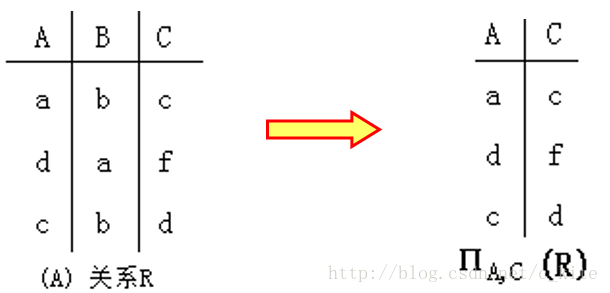
投影(Project,表示为π):从表中抽取特定的列值。
表达式:πM(R)={ t(M) |t∈R }.
释义:R表示一个关系表;
T表示R中的一条横向的记录;
M表示T中的M列的交叉属性值;
πM(R)={ t(M) |t∈R }表示在关系表R中T行M列的一个属性值;
选择(Select,表示为σ–Sigma):从表中选取与给定条件相符的行。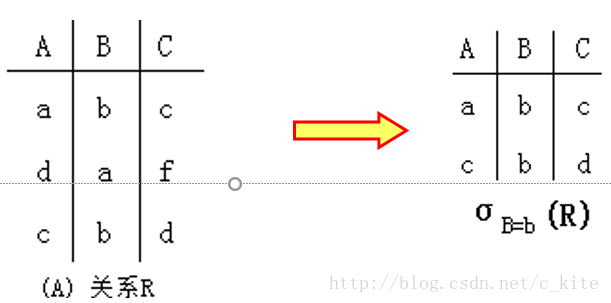
表达式:σA=a(R)={ t(A)=a |t∈R }.
A表示R表中的一个字段或属性类型;
t∈R表示R表中的一条记录;
t(A)=a表示记录t中A属性的具体值等于a;
σA=a(R)={ t(A)=a |t∈R }表示在R表中选择A=a的一条记录;
联接(join,表示为▷◁):通过共同属性连接两个表。
连接运算中有两种最为常见的连接。一种是等值连接还有一种为自然连接。等值连接为从R和S的笛卡尔积中选取那些R和S的公共属性值都相等的那些元组,进行等值连接。
自然连接是一种特殊的等值连接,在等值连接的基础上去掉那些R和S都有的公共属性列,就是自然连接。
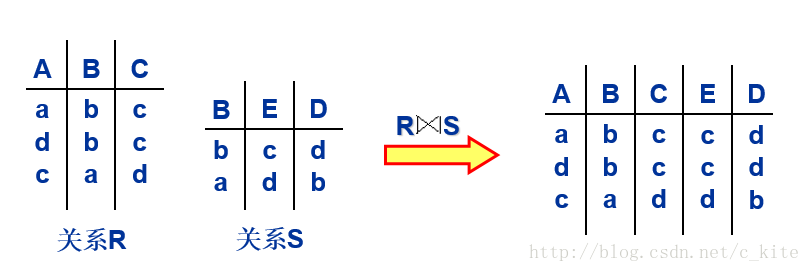
表现在数据库中简单来说是通过字段值相同的条件下,将两个表中的记录连接在一起。
除(Division,表水为÷):除运算需要满足两个条件:表R和表S的属性集合要有相同性;R÷S的商是R和S非相同属性集合的一个投影的子集,该子集和S的笛卡尔积必须包含在R中。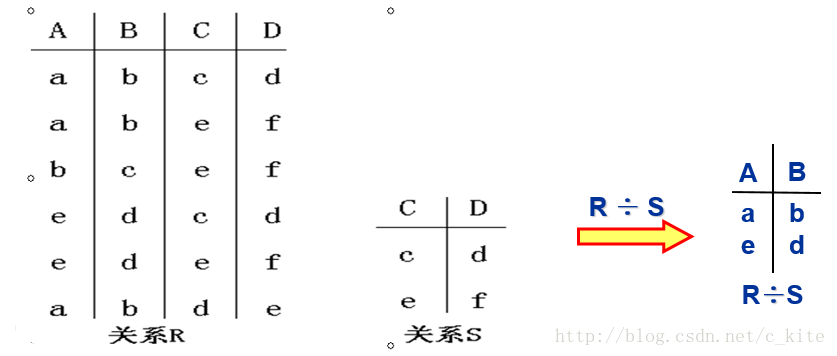
最后
以上就是光亮诺言最近收集整理的关于关系运算的全部内容,更多相关关系运算内容请搜索靠谱客的其他文章。








发表评论 取消回复