通信原理教程chapter4
感冒+繁忙著
教材用的是《通信原理教程》(第三版)–樊昌信著
第四章 模拟信号的数字化
文章目录
- 通信原理教程chapter4
- 抽样
- 低通模拟信号的抽样
- 带通抽样定理
- 量化
- 均匀量化
- 非均匀量化
- 编码
- 脉冲编码调制(PCM)
- 自然二进制码和折叠二进制码
- 编码方式
- 量化噪声
- 增量调制
- 增量调制的量噪比
- 结语
模拟信号的数字化(AD转换)
模电里面也说过,AD转换包括三个基本步骤:抽样,量化,编码,前两个在模电和信号与系统里面其实已经讲得7788了,这章的重点在于基带信号的编码.还有一些就是带通信号的抽样频率,抽样信号的非均匀量化这两个新一点的东西.
这里我们顺便帮大家复习一下信号的分类,当初看见这个图的时候,对在写的这篇blog帮助很大.务必看到每个过程中的信号是连续还是离散的
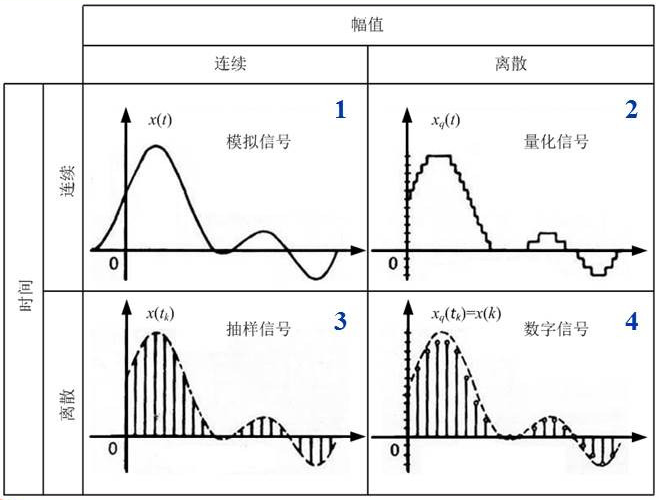
抽样
低通模拟信号的抽样
就是信号与系统学的抽样定理:
2
f
H
≤
f
s
2f_H leq f_s
2fH≤fs
其中,
f
s
f_s
fs被称为奈奎斯特(Nyquist)抽样速率,当
f
s
f_s
fs低于
2
f
H
2f_H
2fH时,重建的信号会产生混叠失真.相关的证明可自行翻阅任意一本信号与系统教材.
带通抽样定理
当我们的输入信号为一个带通信号时,显然此时的抽样频率应与信号带宽有关,而不是简单粗暴地取上限频率的两倍,这里贴一个小教程:
先从低频信号开始讲起:
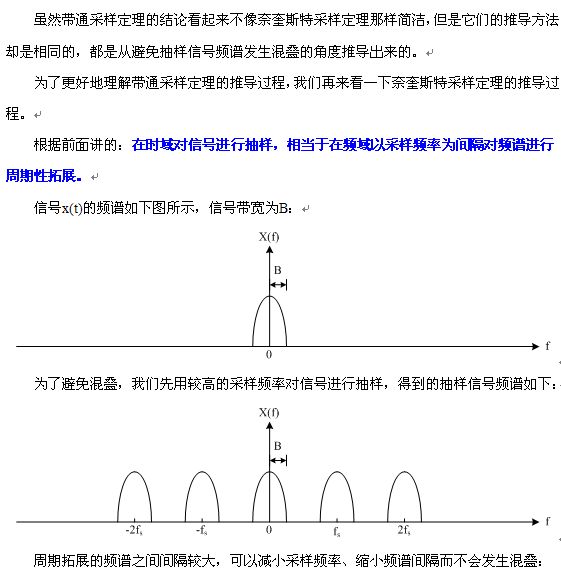
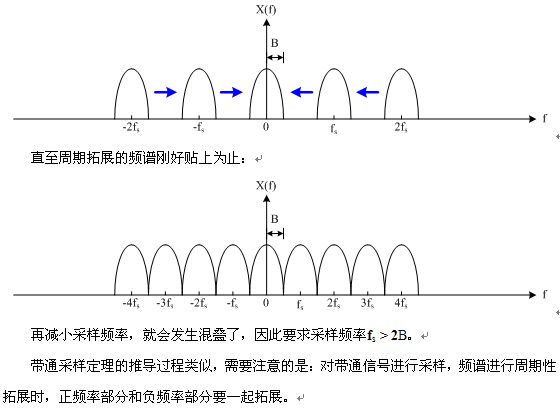
在带通采样定理中,如果要将基带信号无失真重建,我们有(和教材稍稍有不同):
2
f
H
m
≤
f
s
≤
2
f
L
m
−
1
frac{2f_H}{m} leq f_s leq frac{2f_L}{m-1}
m2fH≤fs≤m−12fL
所以下半部分的教程是:
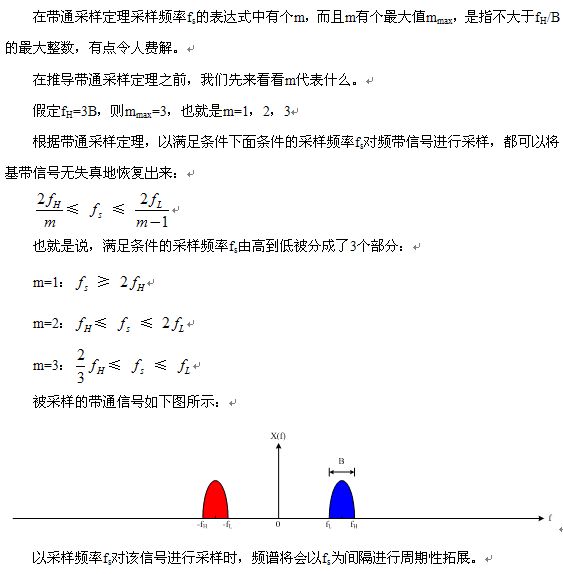
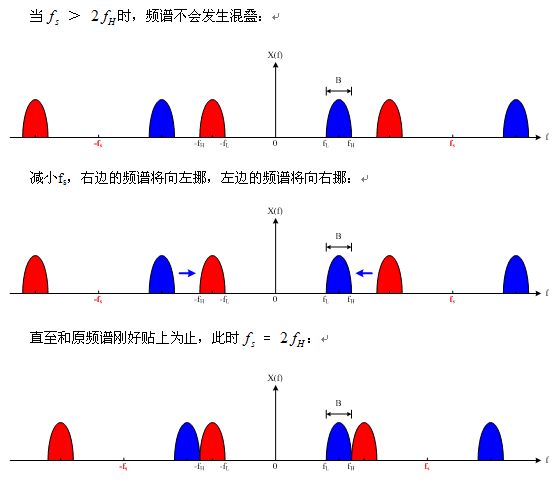
在此基础上我们来推导一下定理和书上写的公式的不同:
书上写的是:
f
s
=
2
B
+
2
k
B
n
=
2
B
(
1
+
k
n
)
fs = 2B + frac{2kB}{n} = 2B(1+frac k n)
fs=2B+n2kB=2B(1+nk)
其中B为信号带宽,
n
=
⌊
f
H
B
⌋
,
0
<
k
<
1
n = lfloor frac {f_H}{B} rfloor quad , quad 0<k<1
n=⌊BfH⌋,0<k<1
书上考虑的是信号恰好不发生混叠的时候,就是定理两个等号取到的时候,下面分两种情况来证明:
- 上限频率是带宽的整数倍
f
H
=
n
B
f_H = nB
fH=nB
此时我们已知的条件有:
f H = n B , f L = ( n − 1 ) B f_H = nB quad ,quad f_L=(n-1)B fH=nB,fL=(n−1)B
只需回代定义式即可得:
f s = 2 B f_s = 2B fs=2B - 上限频率不是带宽的整数倍
f
H
=
n
B
+
k
B
,
0
<
k
<
1
f_H = nB + kB quad , quad 0<k<1
fH=nB+kB,0<k<1
此时我们已知的条件有:
f H = n B ( 1 + k n ) , f L = f H − B f_H = nB(1 + frac k n) quad ,quad f_L=f_H -B fH=nB(1+nk),fL=fH−B
同理带回公式可得:
f s = 2 B ( 1 + k n ) f_s = 2B(1 + frac k n) fs=2B(1+nk)
所以我们可以把第一种情况并入到第二种情况,即k=0,所以有:
f
s
=
2
B
(
1
+
k
n
)
,
0
≤
k
<
1
f_s = 2B(1 + frac k n) quad ,quad 0leq k <1
fs=2B(1+nk),0≤k<1
在计算的时候,由于k也是一个变量,所以我们只需要联立:
{
f
s
=
2
B
(
1
+
k
n
)
f
H
=
n
B
(
1
+
k
n
)
n
=
⌊
f
H
B
⌋
begin{cases} f_s = 2B(1 + frac k n) \ f_H = nB(1+frac k n) \ n = lfloor frac {f_H}{B} rfloor end{cases}
⎩⎪⎨⎪⎧fs=2B(1+nk)fH=nB(1+nk)n=⌊BfH⌋
即可算出
f
s
f_s
fs
量化
看第一张图,这个时候是讲幅值离散化.
均匀量化
这个概念大家应该都懂,这里介绍一下他的量化误差和相应的量噪比
考虑量化电平的间隔,设取值范围为(a,b),量化电平数为M,则有量化间隔:
△
v
=
(
b
−
a
)
/
M
triangle v = (b-a)/M
△v=(b−a)/M
不妨取取值范围为(-a,a),量化电平为M位,考虑其量化误差:
N
q
=
E
[
(
s
k
−
s
q
)
2
]
=
∫
−
a
a
f
(
s
k
)
d
s
k
=
∑
i
=
1
M
∫
m
i
−
1
m
i
(
s
k
−
s
q
)
2
f
(
s
k
)
d
s
k
N_q = E[(s_k - s_q)^2] = int^a_{-a}f(s_k)ds_k =sum^M_{i=1}int^{m_i}_{m_i-1} (s_k - s_q)^2f(s_k)ds_k
Nq=E[(sk−sq)2]=∫−aaf(sk)dsk=i=1∑M∫mi−1mi(sk−sq)2f(sk)dsk
其中:
N
q
N_q
Nq为量化噪声功率的平均值
s
k
s_k
sk为信号的抽样值,即s(kT)
s
q
s_q
sq为量化信号值,即
s
q
(
k
T
)
s_q(kT)
sq(kT)
f
(
s
k
)
f(s_k)
f(sk)为信号抽样值
s
k
s_k
sk的概率密度
m
i
=
−
a
+
i
△
v
,
q
i
=
a
+
i
△
v
−
△
v
2
m_i = -a+itriangle v quad , quad q_i=a+itriangle v-frac {triangle v}2
mi=−a+i△v,qi=a+i△v−2△v
不妨往下化简:
N
q
=
∑
i
=
1
M
∫
m
i
−
1
m
i
(
s
k
−
s
q
)
2
f
(
s
k
)
d
s
k
=
∑
i
=
1
M
∫
m
i
−
1
m
i
(
s
k
−
q
i
)
2
(
1
2
a
)
d
s
k
=
∑
i
=
1
M
∫
−
a
+
(
i
−
1
)
△
v
−
a
+
i
△
v
(
s
k
+
a
−
i
△
v
+
△
v
2
)
2
(
1
2
a
)
d
s
k
=
∑
i
=
1
M
(
1
2
a
)
(
△
v
2
12
)
=
M
(
△
v
)
3
24
a
N_q =sum^M_{i=1}int^{m_i}_{m_i-1} (s_k - s_q)^2f(s_k)ds_k \=sum^M_{i=1}int^{m_i}_{m_{i-1}}(s_k-q_i)^2(frac1{2a})ds_k \=sum^M_{i=1}int^{-a+itriangle v}_{-a+(i-1)triangle v}(s_k+a-itriangle v+frac{triangle v}2)^2(frac1{2a})ds_k \ =sum^M_{i=1}(frac1{2a})(frac{triangle v^2}{12})=frac{M(triangle v)^3}{24a}
Nq=i=1∑M∫mi−1mi(sk−sq)2f(sk)dsk=i=1∑M∫mi−1mi(sk−qi)2(2a1)dsk=i=1∑M∫−a+(i−1)△v−a+i△v(sk+a−i△v+2△v)2(2a1)dsk=i=1∑M(2a1)(12△v2)=24aM(△v)3
由于
M
△
v
=
2
a
Mtriangle v = 2a
M△v=2a,所以有:
N
q
=
(
△
v
)
2
12
N_q = frac{(triangle v)^2}{12}
Nq=12(△v)2
另外,信号功率有:
S
=
E
(
s
k
2
)
=
∫
−
a
a
s
k
2
f
(
s
k
)
d
s
k
S = E(s_k^2) = int^a_{-a}s_k^2f(s_k)ds_k
S=E(sk2)=∫−aask2f(sk)dsk
代入即可以得到:
S
=
∫
−
a
a
s
k
2
(
1
2
a
)
d
s
k
=
M
2
12
(
△
v
)
2
S = int^a_{-a} s_k^2(frac1{2a})ds_k = frac{M^2}{12}(triangle v)^2
S=∫−aask2(2a1)dsk=12M2(△v)2
不把他们合起来是为了计算信噪比:
S
/
N
q
=
M
2
S/N_q = M^2
S/Nq=M2
(
S
/
N
q
)
d
B
=
20
lg
M
(S/N_q)_{dB} = 20lg M
(S/Nq)dB=20lgM
这里结论需要知道.
非均匀量化
显然,在均匀量化中,我们策略并不能很好的保存数据中的细节部分,我们最好做到信号抽样值小的时候,取小的量化间隔,在抽样值大的时候,量化间隔也变大.
这里由于篇幅的原因就直接上结论了,对应书本P75,我们所需要知道的是,为了对不同信号强度保持信号量噪比恒定,在理论上要求压缩特性为对数特性
国际上有两种不同的对数压缩律及其对应的近似算法:
- A压缩律(13折线法),被大陆,欧洲,国际互联时使用
- μ mu μ压缩律(15折线法),被北美,日韩等国家和地区使用
上面的分区会一直看见的.
下面来讲一下A压缩率和13折线法
A压缩律是这样子的,相关为什么A压缩率可以使信号量噪比基本保持恒定的证明可以看书上.
y
=
{
A
x
1
+
ln
A
0
<
x
⩽
1
A
1
+
ln
A
x
1
+
ln
A
1
A
⩽
x
⩽
1
y = left{ begin{array} { l l } { frac { A x } { 1 + ln A } } & { 0 < x leqslant frac { 1 } { A } } \ { frac { 1 + ln A x } { 1 + ln A } } & { frac { 1 } { A } leqslant x leqslant 1 } end{array} right.
y={1+lnAAx1+lnA1+lnAx0<x⩽A1A1⩽x⩽1
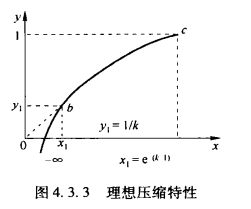
图长这样.
在我国,A的值为87.6
13折线率是A压缩律的一个近似算法,需要近似的原因很简单,因为A压缩律是一个连续的平滑曲线,所以他是很难用电路的方法表征出来的.
13折线律就是以2为底的指数(0-1)取点来提供非均匀部分,每个段落之间取均匀量化.除了第一段和第二段的斜率一样之外,其余的以2为倍数变化.
图长这样
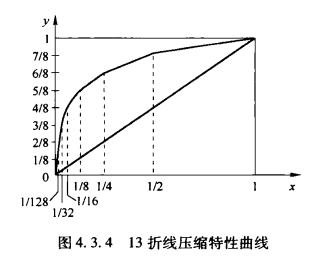
和A压缩律的比较也在这里,注意看i和y的关系,后面讲到PCM编码的时候会回来这里
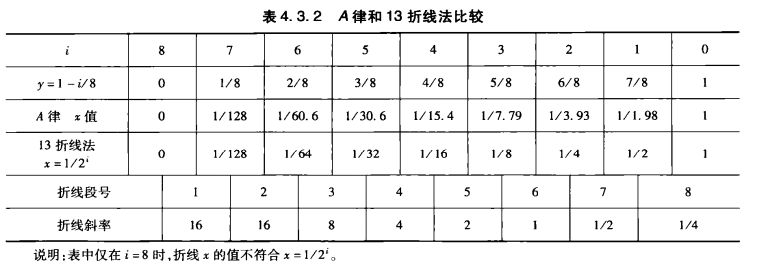
后面讲到PCM编码的时候会加深这里的理解,别慌.
编码
终于介绍到这里重点了,不过也是很简单的概念而已
从开篇的第一张图我们就可以知道,编码其实就是将量化出来之后,他在时间上其实是连续的,这个时候我们需要对他编码的话,第一步就是要让他在时间上离散化,也就是抽样.第二部才是对抽样值进行编码
脉冲编码调制(PCM)
脉冲编码调制PCM(pulse code modulation),其实就是在量化的基础上直接加上抽样而已,用信号与系统的概念来讲就是,拿一个脉冲信号取采样量化信号而已.
下面看编码方式之前,先有一个概念
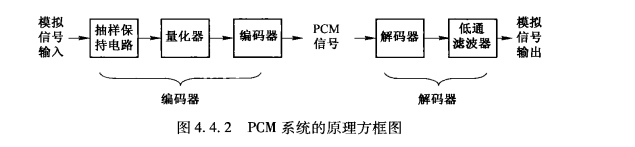
自然二进制码和折叠二进制码
从实现来说,折叠二进制码其实就是自然二进制码的反码,我们可以把最高位看作符号位,将整体减8就可以用上面的方法理解了
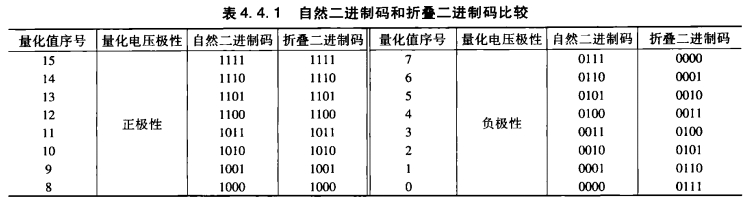
从定义上来看的话,其实很简单,他就相当于讲低8段折反,就相当于以7/8为0,向正负边拓展(因为0000和1000都是0,如果将最高位看成符号位的话),可以看出PCM对小信号的较为有利.
编码方式
总的来说是这样的,具体方式见下下图
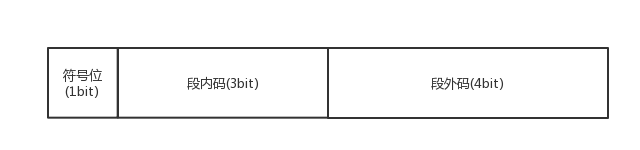
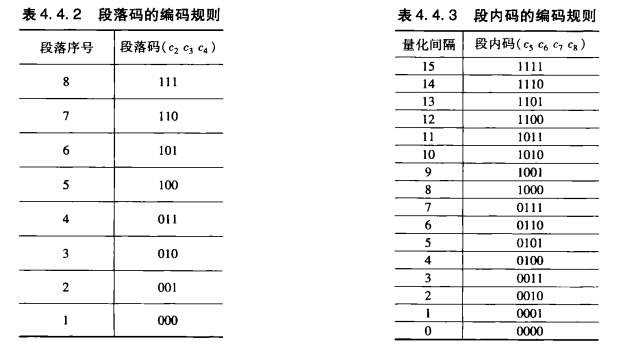
这里在我们计算模拟值转成PCM的时候就不要翻回去看13折线是怎样的了,我们只要知道13折线是以2位底数选出来的,所以我们只要知道这个值在2的负几次幂之间,+8取小的就是他的段落码了,+8其实是因为前面说的i和y的关系导致的.又因为段内码是均匀量化的,所以我们只需要算一下比例取整就可以了,所以,流程如下:
-
确定符号位,肉眼可见
-
确定模拟值的在2的负几次幂之间,比如:
x
∈
(
2
−
8
+
M
,
2
−
8
+
(
M
+
1
)
)
xin (2^{-8+M},2^{-8+(M+1)})
x∈(2−8+M,2−8+(M+1))
这个时候M就是段落码了(M+1是段落序号,小心)
- 对他取比例再量化成4位
n = [ x − 2 − 8 + M 2 − 8 + M ∗ 2 4 ] n = [frac{x-2^{-8+M}}{2^{-8+M}} * 2^4 ] n=[2−8+Mx−2−8+M∗24]
量化噪声
这里不详细讲:
S
/
N
q
=
2
2
(
B
/
f
H
)
S/N_q = 2^{2(B/f_H)}
S/Nq=22(B/fH)
###差分脉冲编码调制DPCM
差分脉冲编码调制DPCM(Differential PCM)其实就是用前几个的抽样值来线性预测后一个抽样值,由于收发两端的预测算法是一样的,得到的信息是一样的,所以解码出来的东西自然一样.
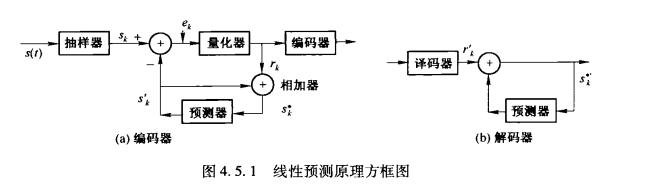
但是我觉得这里教材写得不伦不类,主要是预测器没有讲清楚,我总觉得这种用二进制来描述预测的东西总有点不太直观,而且线性预测也太鸡肋了,理论上应是用上自适应算法(那就变成ADPCM了,这里的A是adaptive)才会有理论应用价值.
基于上面的原因,DPCM和后面的增量调制我都不太详细讲了.就简单介绍一下信噪比算了
####DPCM的量噪比
S
/
N
q
=
3
N
(
M
−
1
)
2
8
π
2
⋅
f
s
3
f
0
2
f
L
S/N_q = frac{3N(M-1)^2}{8pi^2}cdot frac{f_s^3}{f_0^2f_L}
S/Nq=8π23N(M−1)2⋅f02fLfs3
增量调制
如果说DPCM是自适应算法的话,其实增量调制就是自适应算法里面的LMS算法,也就是最简单的一个预测算法.
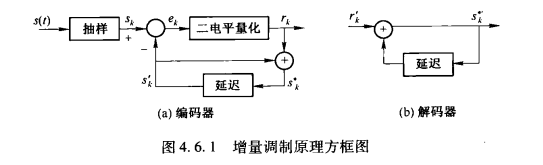
相当于把预测的信息量只要1和0来描述你是比我高还是比我低,高我就加一,低我就减一,简单.
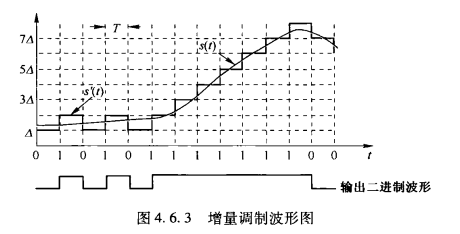
但是实际上会有一个问题就是不能处理非平稳信号,因为突变的频率太快或者幅度太大的话都不会被检测到,又或者根本就跟不上变化.
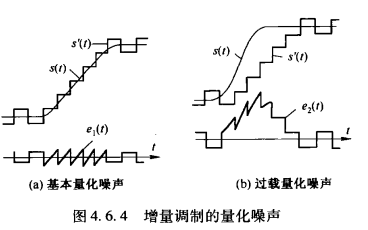
增量调制的量噪比
不作介绍
S
m
a
x
N
q
=
3
8
π
2
⋅
f
s
3
f
0
2
f
L
frac{S_{max}}{N_q} = frac3{8pi^2} cdot frac{f_s^3}{f_0^2f_L}
NqSmax=8π23⋅f02fLfs3
结语
这篇博客的前半部分其实很早就写好了,但是后面因为太忙了一直没有写下去,过完这个双11又要开启更加繁忙的科研生活了,所以相应的进度是真的堪忧了哈哈哈哈哈哈哈哈哈哈哈,又或者要寻找一个同学合作才行了.
本来是想时间太紧,45章合在一起写的.无奈写的时候觉得想讲的东西太多,但是又没有时间.所以没办法,只能把他们分开写了.
然后这里的公式用了一个神器:mathpix来识别的,不用再自己一个一个敲了,大大节省了时间.
最后
以上就是昏睡黑米最近收集整理的关于通信原理教程chapter4通信原理教程chapter4的全部内容,更多相关通信原理教程chapter4通信原理教程chapter4内容请搜索靠谱客的其他文章。








发表评论 取消回复