模拟信号的数字化处理

一、概述

    对于一般的模拟信号，其时域与频域波形均为连续无限长，而若要对信号进行数字处理，必须先将模拟信号进行数字化，即变成计算机可以处理的有限长离散的序列。

    数字化处理分两步，第一步是时域离散化，即时域采样（CTFT->DTFT），第二步是频域离散化，即频域采样（DTFT->DFT）。

二、模拟信号的数字化处理

注：以下讨论均价假设原信号为带限信号，截止频率为Ωm。

1.时域离散化（时域采样）

对连续信号ga(t)进行冲击采样，采样频率为Ωs（采样周期为T），即Ωs≥2Ωm，满足Nyquist采样定理。根据模拟信号时域采样一文可以知道，若设采样信号为gp(t)，其频域响应为Gp(jΩ)，那么可得:

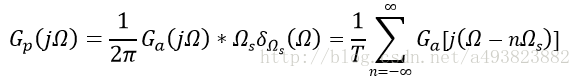
由此可得，取样后的频谱变为周期函数，周期为T，而且幅度变为原来的1/T。

根据离散时间傅里叶变换一文，Gs(jΩ)还可以写作：

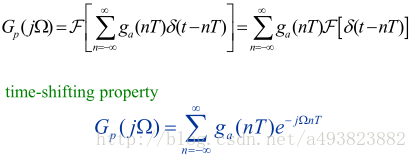
将其写作DTFT（G(ejω））形式得到：

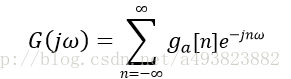
其周期为2π。

根据CTFT与DTFT的关系，我们可以得出结论，对信号ga(t)进行时域离散化（即DTFT），其幅度变为原来的1/T（T为采样周期，满足Nyquist采样定理），一般的，Ω（CTFT频率）与ω（DTFT频率）的对应关系为：

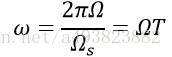
2.频域离散化（频域采样）

由离散傅里叶变换一文可知，频域离散化（DFT）即将CTFT在区间0≤ω≤2π等间隔采样N个点得到的，即间隔为2π/N，即DFT为：

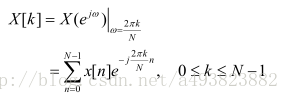
那么DTFT到DFT的频率映射关系为：

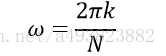
3.信号的时域频域离散化，CTFT->DFT

若设采样频率为Ωs，对应采样周期为T，根据前两节CTFT与DTFT、DTFT与DFT的频率映射关系和幅度变化，我们可以得到：信号经过离散化，连续频率ω与离散频率k的映射关系为：

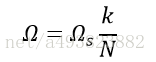
幅度变为原来的1/T，即fs倍。

具体转换如下图例：

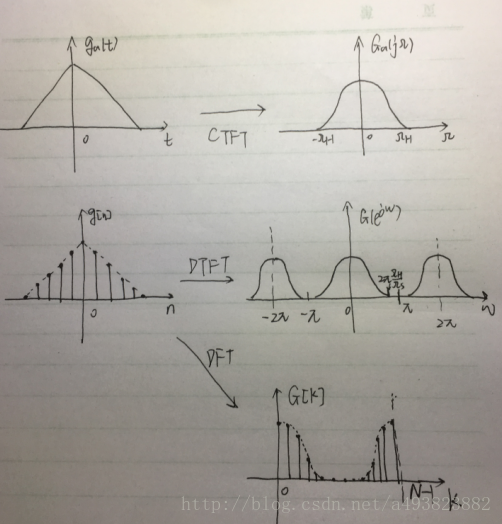
最后

以上就是友好金毛为你收集整理的模拟信号的数字化处理的全部内容，希望文章能够帮你解决模拟信号的数字化处理所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。