将模拟信号经过采样和量化编码形成数字信号,再采用数字信号处理技术进行处理,处理完毕,如果需要,再转换成模拟信号。这种方法称为模拟信号数字处理方法,框图如下:

采样定理及A/D转换
对模拟信号进行采样可以看做一个模拟信号通过一个电子开关S。设电子开关每隔周期T合上一次,每次合上时间为$tau ( ( (tau $ <<T),在电子开关输出端得到其采样信号 x ^ a ( t ) hat x _a(t) x^a(t)。该电子开关的作用等效成一宽度为 τ tau τ,周期为 T T T的矩形脉冲串 p T ( t ) p_T(t) pT(t),采用信号 x ^ a ( t ) hat x _a(t) x^a(t)就是 x a ( t ) x_a(t) xa(t)与 p T ( t ) p_T(t) pT(t)相乘的结果。采样过程下图(a)所示,如果让电子开关合上的时间 τ → 0 tau rightarrow 0 τ→0,则形成理想采样,此时上面的脉冲串变成单位冲激串,用 p a ( t ) p_a(t) pa(t)表示。 p a ( t ) p_a(t) pa(t)中每个单位冲激处在采样点上,强度为1,理想采样则是 x a ( t ) x_a(t) xa(t)与 p δ ( t ) p_{delta}(t) pδ(t)相乘的结果,采样过程如下图(b)所示。
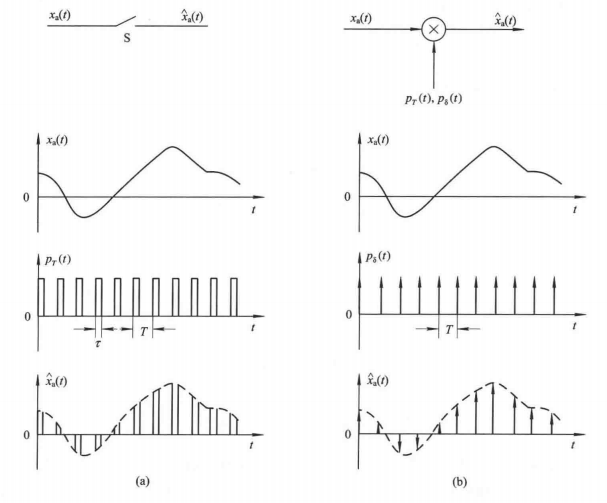
用公式表示为:
p δ ( t ) = ∑ n = − ∞ ∞ δ ( t − n T ) p_delta (t)=sum_{n=-infty}^{infty}delta(t-nT) pδ(t)=∑n=−∞∞δ(t−nT)
x ^ a ( t ) = x a ( t ) p δ ( t ) = ∑ n = − ∞ ∞ x a ( t ) δ ( t − n T ) hat x_a(t) = x_a(t)p_delta (t)=sum_{n=-infty}^{infty}x_a(t)delta(t-nT) x^a(t)=xa(t)pδ(t)=∑n=−∞∞xa(t)δ(t−nT)
上式中 δ ( t ) delta (t) δ(t)是单位冲激信号,在上式中只有当 t = n T t=nT t=nT时,才可能有非零值,因此写成下式:
x ^ a ( t ) = ∑ n = − ∞ ∞ x a ( n T ) δ ( t − n T ) hat x_a(t)=sum_{n=-infty}^{infty}x_a(nT)delta(t-nT) x^a(t)=∑n=−∞∞xa(nT)δ(t−nT)
在傅里叶变换中,两信号在时域乘积的傅里叶变换等于两个信号分别的傅里叶变换的卷积,推导如下:
X a ( j Ω ) = F T [ x a ( t ) ] X_a(jOmega)=FT[x_a(t)] Xa(jΩ)=FT[xa(t)]
X ^ a ( j Ω ) = F T [ x ^ a ( t ) ] hat X_a(jOmega)=FT[hat x_a(t)] X^a(jΩ)=FT[x^a(t)]
P a ( j Ω ) = F T [ p a ( t ) ] P_a(jOmega)=FT[p_a(t)] Pa(jΩ)=FT[pa(t)]
对 p δ ( t ) = ∑ n = − ∞ ∞ δ ( t − n T ) p_delta (t)=sum_{n=-infty}^{infty}delta(t-nT) pδ(t)=∑n=−∞∞δ(t−nT)进行傅里叶变换,得到
P a ( j Ω ) = ∑ k = − ∞ ∞ 2 π a k δ ( Ω − k Ω s ) P_a(jOmega)=sum_{k=-infty}^{infty}2pi a_k delta(Omega - kOmega _s) Pa(jΩ)=∑k=−∞∞2πakδ(Ω−kΩs) 利用的是周期信号的傅里叶变换公式
式中, Ω s = 2 π / T Omega _s=2pi /T Ωs=2π/T,称为采样角频率,单位时 r a d / s rad/s rad/s
a k = 1 T ∫ − T / 2 T / 2 δ ( t ) e − j k Ω s t d t = 1 T a_k=frac{1}{T}int _{-T/2} ^{T/2}delta (t)e^{-jkOmega _s t}dt = frac{1}{T} ak=T1∫−T/2T/2δ(t)e−jkΩstdt=T1
因此,
P a ( j Ω ) = 2 π T ∑ k = − ∞ ∞ δ ( Ω − k Ω s ) P_a(jOmega)=frac{2pi}{T}sum_{k=-infty}^{infty}delta(Omega - kOmega _s) Pa(jΩ)=T2π∑k=−∞∞δ(Ω−kΩs)
利用的是频域卷积定理,两信号在时域相乘的傅里叶变换等于两个信号分别的傅里叶变换的卷积
$$
begin{split}
hat X _a(jOmega) & = frac{1}{2pi}X _a(jOmega)*P _a(jOmega)
&=frac{1}{2pi}bullet frac{2pi}{T}int_{-infty}{infty}X_a(jtheta)sum_{k=-infty}{infty}delta(Omega-kOmega_s-theta)dtheta
&=frac{1}{T}int_{-infty}{infty}X_a(jtheta)sum_{k=-infty}{infty}delta(Omega-kOmega_s-theta)dtheta
&=frac{1}{T}sum_{k=-infty}^{infty}X_a(jOmega-jkOmega_s)
end{split}
$$
上式表明理想采样信号的频谱是原模拟信号的频谱沿频率轴,每间隔采样角频率 Ω s Omega _s Ωs重复出现一次,并叠加形成的周期函数。
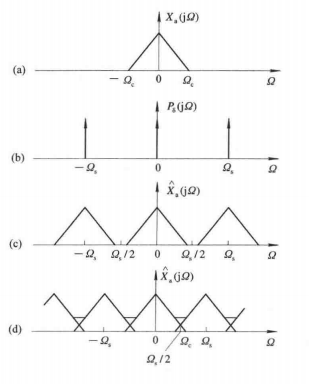
在下图中,设 x a ( t ) x_a(t) xa(t)是带限信号(带宽有限的信号),最高频率为 Ω c Omega_c Ωc,其频谱 X a ( j Ω ) X_a(jOmega) Xa(jΩ)如下图(a)所示,$p_delta (t) 的 频 谱 的频谱 的频谱P_ delta (j Omega ) 如 下 图 ( b ) 所 示 , 如下图(b)所示, 如下图(b)所示,hat x_a(t) 的 频 谱 的频谱 的频谱hat X_a(jOmega) 如 下 图 ( c ) 所 示 , 图 中 原 模 拟 信 号 的 频 谱 称 为 基 带 频 谱 。 如 果 满 足 如下图(c)所示,图中原模拟信号的频谱称为基带频谱。如果满足 如下图(c)所示,图中原模拟信号的频谱称为基带频谱。如果满足Omega _s ge 2Omega_c , 或 者 用 频 率 表 示 该 式 , 即 满 足 ,或者用频率表示该式,即满足 ,或者用频率表示该式,即满足F_sge 2f_c , 基 带 谱 与 其 他 周 期 延 拓 形 成 的 谱 不 重 叠 , 如 下 图 ( c ) 所 示 , 如 果 采 样 频 率 太 低 , 或 者 信 号 最 高 截 止 频 率 过 高 , 使 ,基带谱与其他周期延拓形成的谱不重叠,如下图(c)所示,如果采样频率太低,或者信号最高截止频率过高,使 ,基带谱与其他周期延拓形成的谱不重叠,如下图(c)所示,如果采样频率太低,或者信号最高截止频率过高,使F_s < 2f_c , , ,X_a(jOmega) 按 照 采 样 频 率 按照采样频率 按照采样频率F_s$周期延拓时,形成频谱混叠,如下图(d)所示
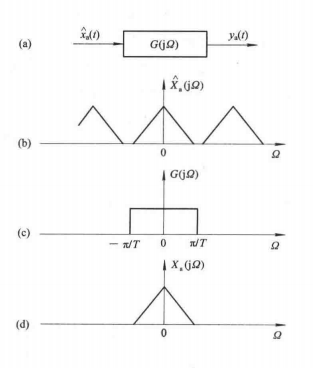
下图时采样恢复
对上述内容总结,采样定理叙述如下:
-
对连续信号进行等间隔采样形成采样信号,采样信号的频谱是原连续信号的频谱以采样频率 Ω s Omega _s Ωs为周期进行周期性的延拓形成的
-
设连续信号 x a ( t ) x_a(t) xa(t)属带限信号,最高截止频率为 Ω c Omega_c Ωc,如果采样角频率 Ω s ≥ 2 Ω c Omega_s ge 2Omega_c Ωs≥2Ωc,那么让采样信号 x ^ ( t ) hat x(t) x^(t)通过一个增益为 T T T、截止频率为 Ω s / 2 = π / T Omega_s/2=pi/T Ωs/2=π/T的理想低通滤波器,可以唯一地恢复出原连续信号 x a ( t ) x_a(t) xa(t)。否则, Ω s ≤ 2 Ω c Omega_s le 2Omega_c Ωs≤2Ωc会造成采样信号中的频谱混叠现象,不可能无失真地恢复原连续信号。
将数字信号转换成模拟信号
将模拟信号 x a ( t ) x_a(t) xa(t)经过理想采样,得到采样信号 x ^ a ( t ) hat x _a(t) x^a(t), x a ( t ) x_a(t) xa(t)和 x ^ a ( t ) hat x _a(t) x^a(t)之间的关系用式 x ^ a ( t ) = ∑ n = − ∞ ∞ x a ( n T ) δ ( t − n T ) hat x_a(t)=sum_{n=-infty}^{infty}x_a(nT)delta(t-nT) x^a(t)=∑n=−∞∞xa(nT)δ(t−nT)表示。如果选择采样频率 F s Fs Fs满足采样定理, x ^ a ( t ) hat x_a(t) x^a(t)的频谱没有频谱混叠现象,可用一个传输函数为 G ( j Ω ) G(jOmega) G(jΩ)的理想低通滤波器不失真地将原模拟信号 x a ( t ) x_a(t) xa(t)恢复出来,这是一种理想恢复。
下式表示低通滤波器的传输函数 G ( j Ω ) G(jOmega) G(jΩ)
G ( j Ω ) = { T , ∣ Ω ∣ < 1 2 Ω s 0 , ∣ Ω ∣ ≥ 1 2 Ω s G(jOmega) = begin{cases} T, & |Omega|<frac{1}{2}Omega_s \[5ex] 0, & |Omega|ge frac{1}{2}Omega_s end{cases} G(jΩ)=⎩⎪⎪⎨⎪⎪⎧T,0,∣Ω∣<21Ωs∣Ω∣≥21Ωs
通过低通滤波器的传输函数 G ( j Ω ) G(jOmega) G(jΩ)推导其单位冲激响应 g ( t ) g(t) g(t):
g ( t ) = 1 2 π ∫ − ∞ ∞ G ( j Ω ) e j Ω t d Ω = 1 2 π ∫ − Ω s / 2 Ω s / 2 T e j Ω t d Ω = s i n ( Ω s t / 2 ) Ω s t / 2 g(t)=frac{1}{2pi}int_{-infty}^{infty}G(jOmega)e^{jOmega t}dOmega = frac{1}{2pi}int_{-Omega_s /2}^{Omega_s /2}Te^{jOmega t}dOmega=frac{sin(Omega_st/2)}{Omega_st/2} g(t)=2π1∫−∞∞G(jΩ)ejΩtdΩ=2π1∫−Ωs/2Ωs/2TejΩtdΩ=Ωst/2sin(Ωst/2)
因为 Ω s = 2 π F s = 2 π / T Omega _s=2pi F_s=2pi/T Ωs=2πFs=2π/T,因此 g ( t ) g(t) g(t)可以表示为
g ( t ) = s i n ( π t / T ) π t / T g(t)=frac{sin(pi t/T)}{pi t/T} g(t)=πt/Tsin(πt/T)
则理想低通滤波器的输入、输出分别为 x ^ a ( t ) hat x_a(t) x^a(t)和 y a ( t ) y_a(t) ya(t),
y a ( t ) = x ^ a ( t ) ∗ y a ( t ) = ∫ x ^ a ( τ ) g ( t − τ ) d τ y_a(t)=hat x_a(t)*y_a(t)=int_{}^{}hat x_a(tau)g(t-tau)dtau ya(t)=x^a(t)∗ya(t)=∫x^a(τ)g(t−τ)dτ
则有
$$
begin{split}
y_a(t)&=int_{-infty}{infty}[sum_{n=-infty}{infty}x_a(nT)delta(t-nT)]g(t-tau)dtau
&=sum_{n=-infty}{infty}int_{-infty}{infty}x_a(nT)delta(t-nT)g(t-tau)dtau
&=sum_{n=-infty}^{infty}x_a(nT)g(t-nT)
&=sum_{n=-infty}^{infty}x_a(nT)frac{sin[pi(t-nT)/T]}{pi(t-nT)/T}
end{split}
$$
由于满足采样定理, y a ( t ) = x a ( t ) y_a(t)=x_a(t) ya(t)=xa(t),因此得到:
x a ( t ) = = ∑ n = − ∞ ∞ x a ( n T ) s i n [ π ( t − n T ) / T ] π ( t − n T ) / T x_a(t)==sum_{n=-infty}^{infty}x_a(nT)frac{sin[pi(t-nT)/T]}{pi(t-nT)/T} xa(t)==∑n=−∞∞xa(nT)π(t−nT)/Tsin[π(t−nT)/T]
式中,当 n = … … , − 1 , 0 , 1 , 2 , … … n=……,-1,0,1,2,…… n=……,−1,0,1,2,……时, x a ( n T ) x_a(nT) xa(nT)是一串离散的采样值,而 x a ( t ) x_a(t) xa(t)是模拟信号, t t t取连续值, g ( t ) g(t) g(t)的波形如下图所示:
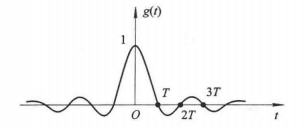
g ( t ) g(t) g(t)保证了在各个采样点上,即 t = n T t=nT t=nT时,恢复的 x a ( t ) x_a(t) xa(t)等于原采样值,而在采样点之间,则是各采样值乘以 g ( t − n T ) g(t-nT) g(t−nT)的波形伸展叠加而成的。这种波形叠加的情况如下图所示。
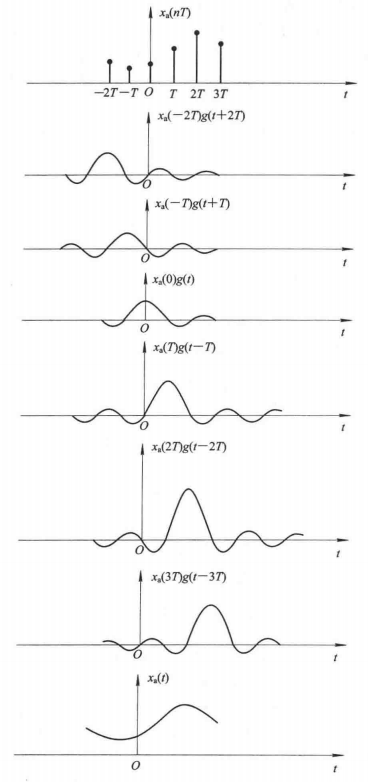
g ( t ) g(t) g(t)函数所起的作用是在各采样点之间内插,因此称为内插函数,而 x a ( t ) = = ∑ n = − ∞ ∞ x a ( n T ) s i n [ π ( t − n T ) / T ] π ( t − n T ) / T x_a(t)==sum_{n=-infty}^{infty}x_a(nT)frac{sin[pi(t-nT)/T]}{pi(t-nT)/T} xa(t)==∑n=−∞∞xa(nT)π(t−nT)/Tsin[π(t−nT)/T]称为内插公式。这种用理想低通滤波器恢复的模拟信号完全等于原模拟信号 x a ( t ) x_a(t) xa(t),是一种无失真的恢复。
参考文献:
- 《数字信号处理》—高西全、丁玉美
最后
以上就是外向河马最近收集整理的关于数字信号处理---模拟信号数字处理方法采样定理及A/D转换将数字信号转换成模拟信号的全部内容,更多相关数字信号处理---模拟信号数字处理方法采样定理及A/D转换将数字信号转换成模拟信号内容请搜索靠谱客的其他文章。








发表评论 取消回复