【压缩感知合集1】(背景知识)香农奈奎斯特采样定理的数学推导和图解分析
【压缩感知合集2】(背景知识)信号稀疏表示的数学推导和解释理解
【压缩感知合集3】压缩感知的背景与意义
【压缩感知合集4】(背景知识)理想采样信号和随机采样信号两种采样信号的频谱分析,以及采样效果比较
香农奈奎斯特采样定理
1 评价
-
支配先阶段几乎所有信号的获取、处理、存储、传输过程。
-
采样后再进行压缩的方式浪费了大量的采样资源, 如果采样后的信号长度仍然很长, 那么变换会消耗很长时间。
-
由于需要保留的 K K K个重要分量的位置是随着信号的不同而不同,所以这种编解码方式是自适应的,需要分配多余的存储空间以保留 K K K个重要分量的位置。
-
K K K个重要分量有可能在传输过程中丢失其中的某几个分量从而造成较差的抗干扰能力。
2 数学解释
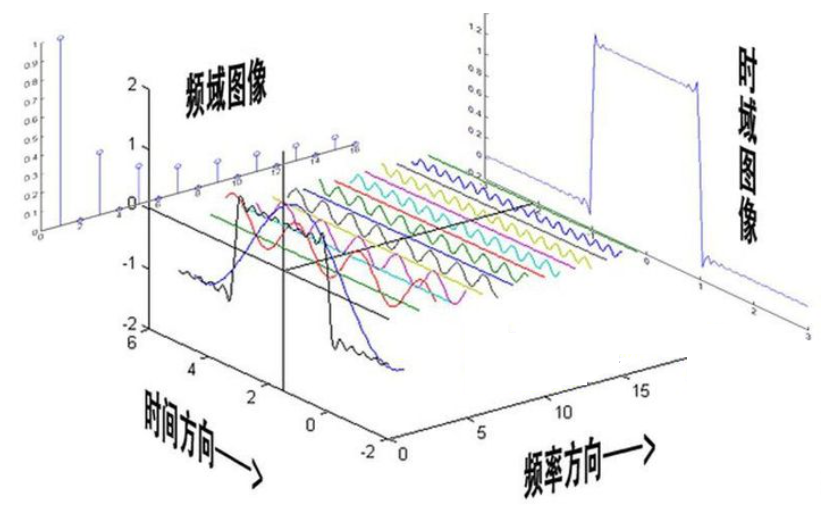
傅里叶分析示意图
数学模型证明
输入连续信号 x a ( t ) x_a(t) xa(t)
采样输出信号 x s ( t ) x_s(t) xs(t)
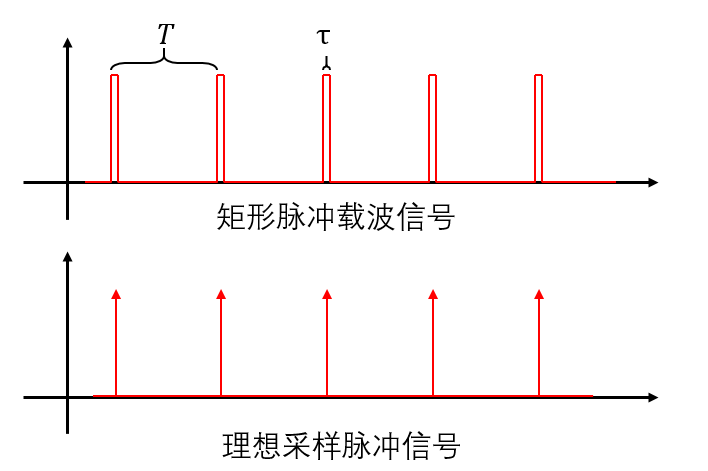
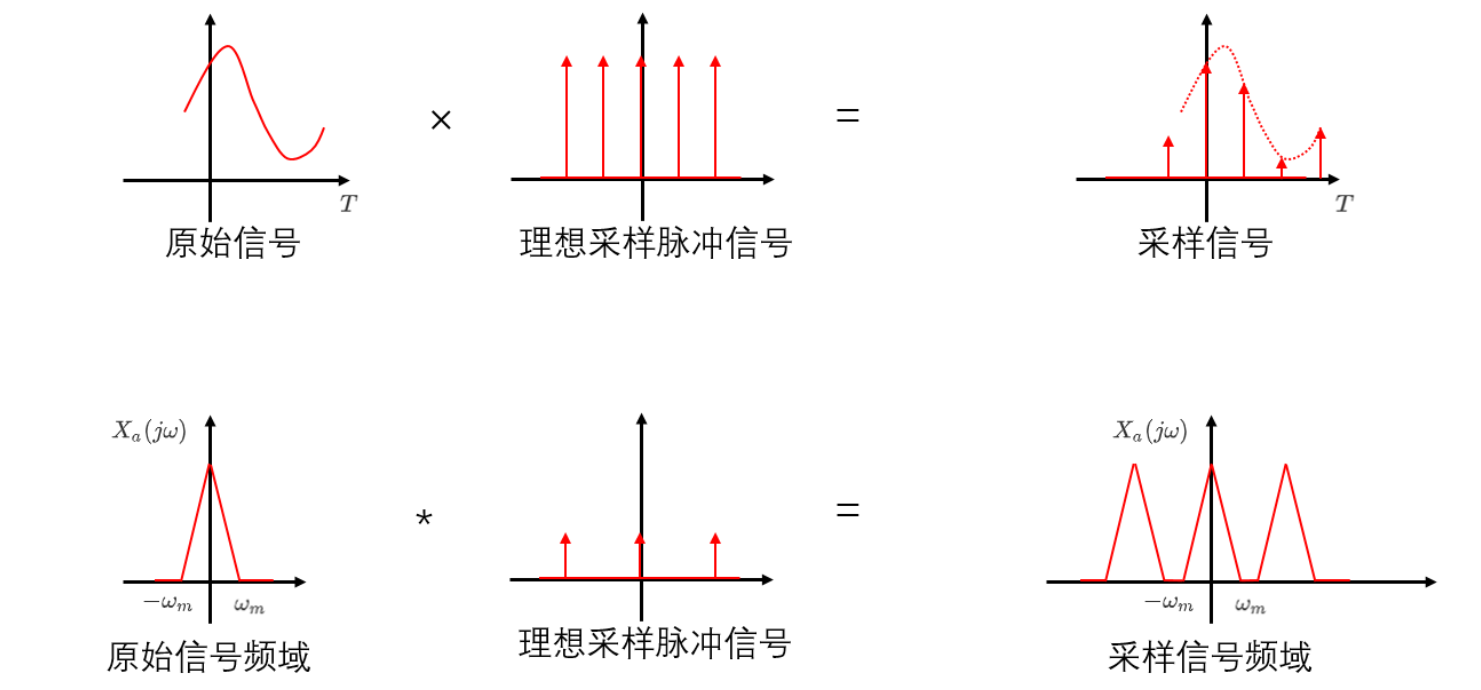
通常意义上采样的过程是一段周期的矩形脉冲载波信号 S ( t ) S(t) S(t),信号周期为 T T T,宽度为 τ tau τ, τ tau τ越小采样越精准(理解:保留的值越接近时序点的对应值),当 τ < < T tau<<T τ<<T的时候,采样脉冲信号接近于 δ delta δ函数信号 S ( t ) = ∑ − ∞ ∞ δ ( t − n T ) S(t)=sum_{-infty}^{infty} delta(t-n T) S(t)=∑−∞∞δ(t−nT)
理想采样
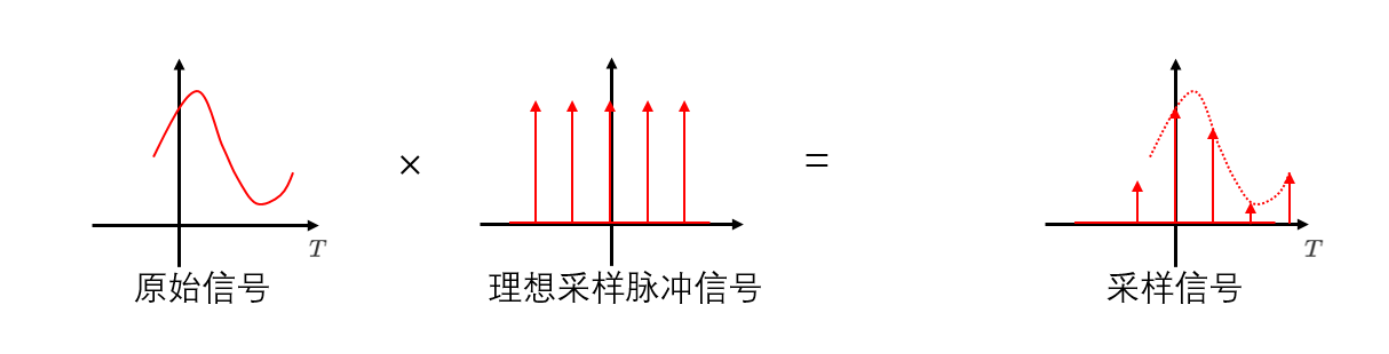
x s ( t ) = x a ( t ) s ( t ) x_{s}(t)=x_{a}(t) s(t) xs(t)=xa(t)s(t)
信号 x a ( t ) x_a(t) xa(t)的傅里叶变换
X a ( j ω ) = ∫ − ∞ ∞ x a ( t ) e − j ω t d t X_{a}(j omega)=int_{-infty}^{infty} x_{a}(t) e^{-j omega t} d t Xa(jω)=∫−∞∞xa(t)e−jωtdt
信号 S ( t ) S(t) S(t)的傅里叶变换
S ( j ω ) = ∫ − ∞ ∞ S ( t ) e − j ω t d t S(j omega)=int_{-infty}^{infty} S(t) e^{-j omega t} d t S(jω)=∫−∞∞S(t)e−jωtdt
信号 x s ( t ) x_s(t) xs(t)的傅里叶变换
X s ( j ω ) = ∫ − ∞ ∞ x s ( t ) e − j ω t d t X_{s}(j omega)=int_{-infty}^{infty} x_{s}(t) e^{-j omega t} d t Xs(jω)=∫−∞∞xs(t)e−jωtdt
对于理想采样 x s ( t ) = x a ( t ) s ( t ) x_{s}(t)=x_{a}(t) s(t) xs(t)=xa(t)s(t) 有时域相乘对应频域卷积
X s ( j ω ) = 1 2 π X a ( j ω ) ∗ S ( j ω ) X_{s}(j omega)=frac{1}{2 pi} X_{a}(j omega) * S(j omega) Xs(jω)=2π1Xa(jω)∗S(jω)
根据补充证明可以知道
S ( j ω ) = 2 π T ∑ k = − ∞ ∞ δ ( ω − k ω s ) S(j omega)=frac{2 pi}{T} sum_{k=-infty}^{infty} deltaleft(omega-k omega_{s}right) S(jω)=T2π∑k=−∞∞δ(ω−kωs)
所以
X
s
(
j
ω
)
=
1
2
π
[
2
π
T
∑
k
=
−
∞
∞
δ
(
ω
−
k
ω
s
)
∗
X
a
(
j
ω
)
]
=
1
T
∫
−
∞
∞
X
a
(
j
θ
)
∑
k
=
−
∞
∞
δ
(
ω
−
k
ω
s
−
θ
)
d
θ
begin{aligned} &X_{s}(j omega)=frac{1}{2 pi}left[frac{2 pi}{T} sum_{k=-infty}^{infty} deltaleft(omega-k omega_{s}right) * X_{a}(j omega)right] \ &=frac{1}{T} int_{-infty}^{infty} X_{a}(j theta) sum_{k=-infty}^{infty} deltaleft(omega-k omega_{s}-thetaright) d theta end{aligned}
Xs(jω)=2π1[T2πk=−∞∑∞δ(ω−kωs)∗Xa(jω)]=T1∫−∞∞Xa(jθ)k=−∞∑∞δ(ω−kωs−θ)dθ
根据冲击函数的性质(见下图的冲激函数示意图)
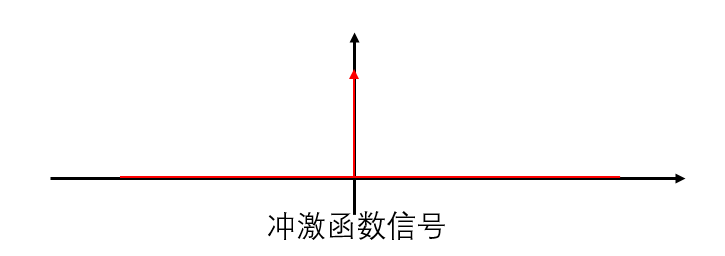
可以得到下面的公式推导
X
s
(
j
ω
)
=
1
T
∑
k
=
−
∞
∞
X
a
(
j
ω
−
j
k
ω
s
)
X_{s}(j omega)=frac{1}{T} sum_{k=-infty}^{infty} X_{a}left(j omega-j k omega_{s}right)
Xs(jω)=T1k=−∞∑∞Xa(jω−jkωs)
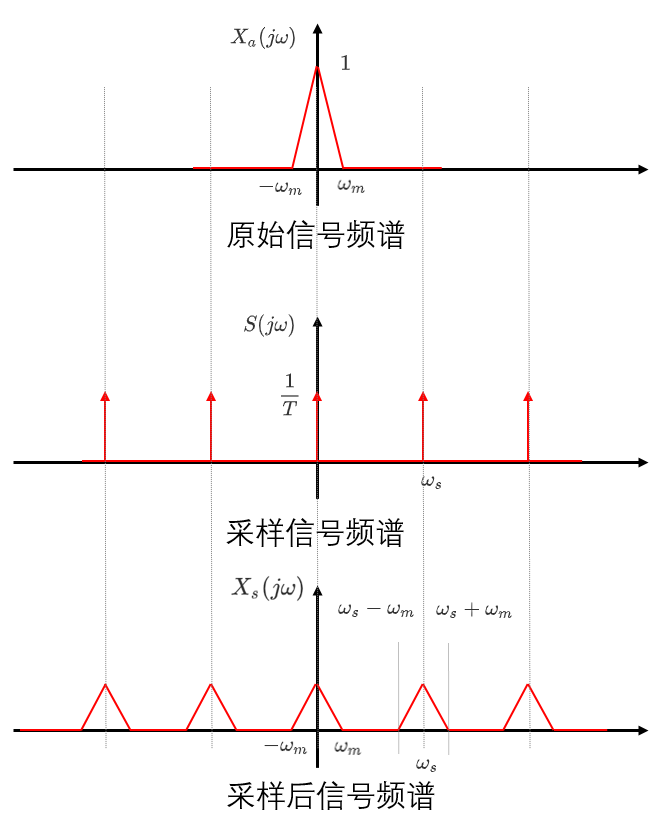
这也就相当于说针对原始被采样信号的频谱做了一个周期延拓,具体可以看如下的示意图
补充说明
每一个周期函数都可以写成完全用傅里叶级数展开的求和形式,将周期采样函数
S
(
t
)
S(t)
S(t)写成如下形式
S
(
t
)
=
∑
k
=
−
∞
∞
a
k
e
j
k
ω
s
t
S(t)=sum_{k=-infty}^{infty} a_{k} e^{j k omega_{s} t}
S(t)=k=−∞∑∞akejkωst
其中
ω
s
=
2
π
T
omega_{s}=frac{2 pi}{T}
ωs=T2π
然后我们求一下傅里叶级数的系数
a
k
=
1
T
∫
−
T
/
2
T
/
2
∑
−
∞
∞
δ
(
t
−
n
T
)
e
−
j
k
ω
s
t
d
t
=
1
T
a_{k}=frac{1}{T} int_{-T / 2}^{T / 2} sum_{-infty}^{infty} delta(t-n T) e^{-j k omega_{s} t} d t=frac{1}{T}
ak=T1∫−T/2T/2−∞∑∞δ(t−nT)e−jkωstdt=T1
发现以采样频率
ω
s
omega_{s}
ωs作为基波的任意整数倍频带内都有相同的能量也就是
1
T
frac{1}{T}
T1在此提一下,正是因为有这个均匀的能量分布才有了后面的周期延拓
傅里叶分解后采样信号的每一个级数分量(在不考虑系数情况下),都是单独频率点唯一的正弦类函数,又因为线性时不变系统的原因,采样信号 S ( t ) S(t) S(t)和被采样信号 x s ( t ) x_{s}(t) xs(t)相乘可以理解为被采样信号的每一个傅里叶级数分量进行分别的调制,而被调制搬移到了不同的频谱。
现在考虑系数理想采样信号,拥有性质:任意傅里叶级数能量相同,所以搬移调制后会有着很好的频谱能量不变性。(即在每一个频率分量段内都保持同等放大缩小幅度)。
继续推导,有了刚才的傅里叶级数的系数,带入傅里叶展开之后再看一次
S
(
t
)
=
1
T
∑
k
=
−
∞
∞
e
j
k
ω
s
t
S(t)=frac{1}{T} sum_{k=-infty}^{infty} e^{j k omega_{s} t}
S(t)=T1k=−∞∑∞ejkωst
有了这个级数展开之后我们去看频域的公式
S
(
j
ω
)
=
∫
−
∞
∞
S
(
t
)
e
−
j
ω
t
d
t
=
∫
−
∞
∞
(
1
T
∑
k
=
−
∞
∞
e
j
k
ω
s
t
)
e
−
j
ω
t
d
t
=
1
T
∑
k
=
−
∞
∞
F
[
e
j
k
ω
s
t
]
begin{aligned} S(j omega)=int_{-infty}^{infty} S(t) e^{-j omega t} d t \=int_{-infty}^{infty} (frac{1}{T} sum_{k=-infty}^{infty} e^{j k omega_{s} t}) e^{-j omega t} d t \=frac{1}{T} sum_{k=-infty}^{infty} Fleft[e^{j k omega_{s} t}right] end{aligned}
S(jω)=∫−∞∞S(t)e−jωtdt=∫−∞∞(T1k=−∞∑∞ejkωst)e−jωtdt=T1k=−∞∑∞F[ejkωst]
由于(其实也就是因为
S
(
t
)
S(t)
S(t)只有固定频率点
k
ω
s
komega_{s}
kωs有能量,其他任何与整数倍
ω
s
omega_{s}
ωs不相同的
ω
omega
ω积分的时候都会变成0)
F
[
e
j
k
ω
s
t
]
=
2
π
δ
(
ω
−
k
ω
s
)
Fleft[e^{j k omega_{s} t}right]=2 pi deltaleft(omega-k omega_{s}right)
F[ejkωst]=2πδ(ω−kωs)
所以
S
(
j
ω
)
=
2
π
T
∑
k
=
−
∞
∞
δ
(
ω
−
k
ω
s
)
S(j omega)=frac{2 pi}{T} sum_{k=-infty}^{infty} deltaleft(omega-k omega_{s}right)
S(jω)=T2πk=−∞∑∞δ(ω−kωs)

总结加图例分析
上半部分是采样过程的时域效果
下半部分是采样过程的频域效果
如果采样频率大于奈奎斯特频率:(可以在低通滤波器后被复原)

采样频率等于奈奎斯特频率:(可以在低通滤波器后被复原)

采样频率小于奈奎斯特频率(就会出现频谱混叠不能实现频谱在采样条件下完全的被分离出来)

如果一个系统以超过信号最高频率至少两倍的速率对模拟信号进行均匀采样,那么原始模拟信号就能从采样产生的离散值中完全恢复。
LAST、参考文献
从理论到实践,奈奎斯特采样定理,我终于闹明白了!-面包板社区
能否简单解释下什么是奈奎斯特–香农采样定理? - 知乎
如何理解 Nyquist 采样定理? - 知乎
最后
以上就是端庄爆米花最近收集整理的关于【压缩感知合集1】(背景知识)香农奈奎斯特采样定理的数学推导和图解分析香农奈奎斯特采样定理1 评价2 数学解释LAST、参考文献的全部内容,更多相关【压缩感知合集1】(背景知识)香农奈奎斯特采样定理的数学推导和图解分析香农奈奎斯特采样定理1内容请搜索靠谱客的其他文章。








发表评论 取消回复