Day13--Simulink仿真设置

该系列博客主要讲述Matlab软件在自动控制方面的应用，如无自动控制理论基础，请先学习自动控制系列博文，该系列博客不再详细讲解自动控制理论知识。
自动控制理论基础相关链接：https://blog.csdn.net/qq_39032096/category_10287468.html?spm=1001.2014.3001.5482
博客参考书籍：《MATLAB/Simulink与控制系统仿真》。

1.控制系统数学模型基础

1.1 动态过程微分方程描述

• 线性系统理论中，常用的数学模型形式有传递函数模型(系统外部模型)、状态方程模型(系统内部模型)、零极点增益模型和部分分式模型；

• 控制系统动态微分方程的建立基于以下两个条件：

  • 在给定量产生变化或扰动出现前，被控制量的各阶导数均为零，即系统处于平衡状态，因此在任一瞬间，由各种不同环节组成的自动控制系统用几个独立变量即可完全确定系统的状态；
  • 建立的动态微分方程式是以微小增量为基础的增量方程，而不是其绝对值的方程，因此，当出现扰动或给定量产生变化时，被控量和各独立变量在其平衡点附近将产生微小的增量，微分方程式描述的是微小偏差下系统运动状态的增量方程，不是运动状态变量的绝对值方程，也不是大偏差范围内的增量方程；

• 动态微分方程描述的是被控量与给定量或扰动量间的函数关系，给定量和扰动量为系统的输入量，被控量为输出量；

• 建立系统微分方程一般步骤：

  • 将系统划分为多个环节，确定各环节的输入及输出信号，每个环节可考虑写一个方程；
  • 根据物理定律或通过实验等方法得出物理规律，列出各环节的原始方程式，并适当简化、线性化；
  • 将各环节方程式联立，消去中间变量，得出只含有输入变量、输出变量及参量的系统方程式；

• 单输入单输出系统微分方程表示的输入模型一般如下形式：
  $$a_0{x}_o^{(n)}(t)+a_1{x}_o^{(n-1)}(t)+\cdots +a_n{x}_o(t)=b_0{x}_i^{(m)}(t)+b_1{x}_i^{(m-1)}(t)+\cdots +b_m{x}_i(t)$$

1.2 拉氏变换与控制系统模型

• 时域函数$f(t)$的拉氏变换定义为：
  $$F(s)={\int }_0^{\infty }f(t){\mathrm{e}}^{-st}\mathrm{d}t$$
  记为：$F(s)=L[f(t)]，s$称为拉氏算子。

• 拉氏变换和拉氏反变换的关系：

  

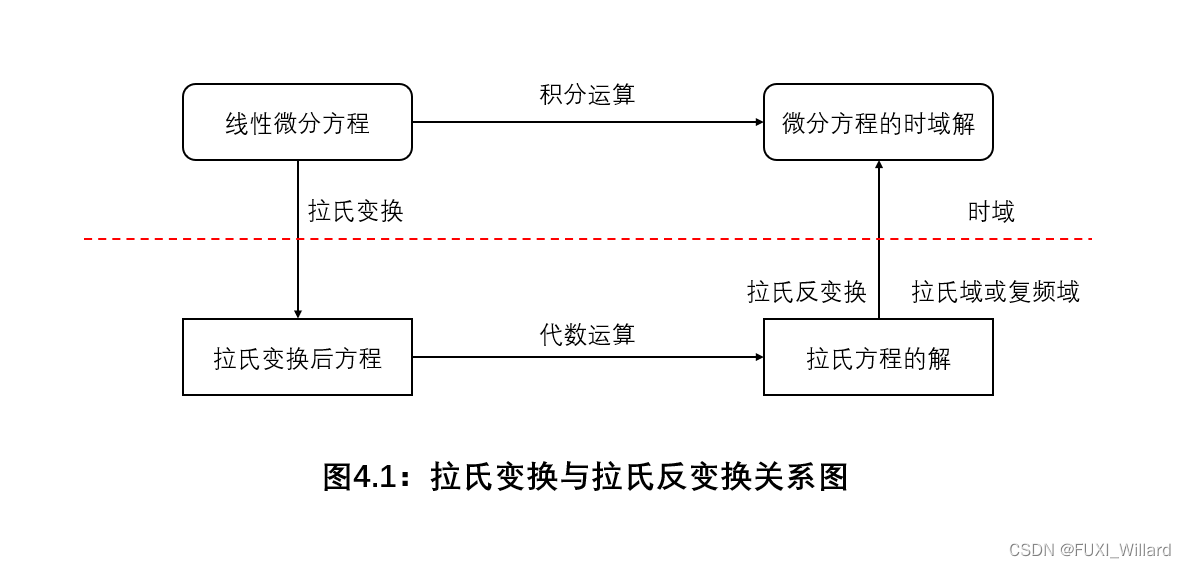
• 拉氏变换基本定理

  $定理$	$原函数f(t)$	$象函数F(s)$
  $线性定理$	$a{f}_1(t)+b{f}_2(t)，a,b为实数$	$a{F}_1(s)+b{F}_2(s)$
  $复平移定理$	${\mathrm{e}}^{\pm at}f(t)$	$F(s\pm a)$
  $复实平移定理$	$f(t-T)$	${\mathrm{e}}^{-Ts}F(s)(T\ge 0)$
  $标尺定理$	$f\left(\frac{t}{a}\right)$	$aF(as)$
  $微分定理$	$\frac{\mathrm{d}}{\mathrm{d}t}f(t)$	$sF(s)-f(0)$
  $微分定理$	$\frac{{\mathrm{d}}^n}{\mathrm{d}{t}^n}f(t)$	$s^{n}F(s)-\sum _{r=1}^n\frac{{\mathrm{d}}^{r-1}}{\mathrm{d}{t}^{r-1}}f(0)s^{n-r}$
  $积分定理$	${\int }_0^{t}f(t)\mathrm{d}t$	$\frac{1}{s}F(s)$
  $卷积定理$	${\int }_0^t{f}_1(\tau )f_2(\tau -t)\mathrm{d}\tau$	$F_1(s)F_2(s)$
  $初值定理$	$\underset{t\to 0}{\lim }[f(t)]=\underset{s\to \infty }{\lim }[sF(s)]=f(0)$
  $终值定理$	$\underset{t\to \infty }{\lim }[f(t)]=\underset{s\to 0}{\lim }[sF(s)]=f(\infty )$

• 常用函数的拉氏变换

  $f(t)$	$F(s)$	$f(t)$	$F(s)$
  $\delta (t)单位脉冲$	$1$	$t$	$\frac{1}{s^2}$
  $u(t)单位阶跃$	$\frac{1}{s}$	$t^n$	$\frac{n!}{s^{n+1}}$
  ${\mathrm{e}}^{at}$	$\frac{1}{s-a}$	$t^n{\mathrm{e}}^{at}$	$\frac{n!}{(s+a{)}^{n+1}}$
  $\cos (\omega t)$	$\frac{s}{(s^2+{\omega }^2)}$	$\sin (\omega t)$	$\frac{\omega }{(s^2+{\omega }^2)}$
  ${\mathrm{e}}^{-at}\cos (\omega t)$	$\frac{s+a}{(s+a{)}^2+{\omega }^2}$	${\mathrm{e}}^{-at}\sin (\omega t)$	$\frac{\omega }{(s+a{)}^2+{\omega }^2}$
  $\frac{1}{b-a}({\mathrm{e}}^{-at}-{\mathrm{e}}^{-bt})$	$\frac{1}{(s+a)(s+b)}$	$\frac{1}{b-a}(b{\mathrm{e}}^{-bt}-a{\mathrm{e}}^{-at})$	$\frac{s}{(s+a)(s+b)}$

• 拉氏反变换定义：
  $$f(t)=\frac{1}{2\pi \mathrm{j}}{\int }_{\sigma -\mathrm{j}\omega }^{\sigma +\mathrm{j}\omega }F(s){\mathrm{e}}^{st}\mathrm{d}s$$
  记为：$f(t)=L^{-1}[F(s)]$。

1.3 数学模型描述

1.3.1 传递函数模型

• 传递函数在拉氏变换的基础上，以系统本身的参数所描述的线性定常系统输入量和输出量的关系式，表达了系统内在的固有特性，与输入量无关；

• 线性定常系统的传递函数定义：在零初始条件下，输出量的拉普拉斯变换与输入量的拉普拉斯变换之比；

• 线性定常系统的微分方程描述：
  $$\begin{array}{rl}& a_0{x}_o^{(n)}(t)+a_1{x}_o^{(n-1)}(t)+\cdots +a_{n-1}{x}_o^{(1)}(t)+a_n{x}_o(t)\\ & \\ =& b_0{x}_i^{(m)}(t)+b_1{x}_i^{(m-1)}(t)+\cdots +b_{m-1}{x}_i^{(1)}(t)+b_m{x}_i(t)，n\ge m\end{array}$$

  • $x_o$：系统的输出量；
  • $x_i$：系统的输入量；
  • $a_0,a_1,\cdots ,a_n；b_0,b_1,\cdots ,b_m$为系数；

• 系统的传递函数描述：
  $$G(s)=\frac{X_o(s)}{X_i(s)}=\frac{b_0{s}^m+b_1{s}^{m-1}+\cdots +b_{m-1}s+b_m}{a_0{s}^n+a_1{s}^{n-1}+\cdots +a_{n-1}s+a_n}$$

• 传递函数的特点：

  • 传递函数比微分方程简单，通过拉氏变换，实数域内复杂的微积分运算转化成代数运算；
  • 当系统输入典型信号时，其输出与传递函数有一定对应关系，当输入是单位脉冲函数时，输入的象函数是$1$，其输出象函数与传递函数相同；
  • 令传递函数中的$s=\mathrm{j}\omega$，则系统可在频域内分析；
  • 传递函数的零极点分布决定系统的动态特性；

• $\mathrm{MATLAB}$表示：
  $$\mathrm{num}=[b_0,b_1,\cdots ,b_m]，\mathrm{den}=[a_0,a_1,\cdots ,a_n]\Rightarrow G(s)=\frac{\mathrm{num}(s)}{\mathrm{den}(s)}$$

1.3.2 零极点形式的数学模型

• 零极点模型是分别对原系统传递函数的分子、分母进行分解因式处理，得到系统零点和极点的表示形式，如下所示：
  $$G(s)=K\frac{(s-z_1)(s-z_2)\cdots (s-z_m)}{(s-p_1)(s-p_2)\cdots (s-p_n)}=\frac{K\prod _{i=1}^m(s+z_i)}{\prod _{j=1}^n(s+p_j)}$$

  • $K$：系统增益；
  • $-z_i(i=1,2,\cdots ,m)$：分子多项式的根，为系统的零点；
  • $-p_j(j=1,2,\cdots ,n)$：分母多项式的根，为系统的极点；

• 传递函数的分母多项式即特征多项式，特征多项式等于零的方程即传递函数的特征方程，特征方程的根即传递函数的极点；

• 传递函数的极点决定了所描述系统的自由运动模态，零点影响各模态在系统响应中所占的比重；

1.3.3 状态空间模型

• 以状态空间理论为基础的现代控制理论的数学模型采用状态空间模型，以时域分析为主，着眼于系统的内部状态及其内部联系；

• 状态是系统动态信息的集合，在表征系统信息的所有变量中，能够全部描述系统运行的最小数目的一组独立变量称为系统的状态变量，选取不唯一；

• 状态方程是由系统状态变量构成的一阶微分方程组；

• 具有$n$个状态、$r$个输入和$m$个输出的线性时不变系统，用矩阵表示的状态空间如下：
  $$\begin{array}{rl}& \dot{x}=Ax+Bu(状态方程)\\ & y=Cx+Du(输出方程)\end{array}$$

  • 状态向量$x$是$n$维；
  • 输入向量$u$是$r$维；
  • 输出向量$y$是$m$维；
  • 状态矩阵$A$是$n\times n$维；
  • 输入矩阵$B$是$n\times r$维；
  • 输出矩阵$C$是$m\times n$维；
  • 前馈矩阵$D$是$m\times r$维；

最后

以上就是直率墨镜为你收集整理的Day13--Simulink仿真设置的全部内容，希望文章能够帮你解决Day13--Simulink仿真设置所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。