概述
LADRC的离散化实现
一、感慨
上一次写博客是两年前了，现在已经过了那么久，期间经历了许多事，有好有坏，不多大多时候是丧的。到了现在，终究让我相通了一件事情，深刻理解并追求自己想要做的事情是会幸福的。通过读了许多书，在b站上看了许多视频，通过自身经历，总结得到了一个学习新的方法，以后还会不断的更新迭代。用模型，抽象的方法来观察和看待这是世界，但是前提我需要理解深刻。因此，在处于还有一年就毕业的状态下，打算恶补计算机知识，先提升自己理解知识的深度和广度，再形成自己看待世界的方法。
为了填补两年前的坑，我在一年半以前把离散化 LADRC 写出来了，但是我在课题中一直没有用上，放着也觉得浪费，因此打算分享出来。期间也看到过别人用 C 语言啊等等写过离散的 ADRC，但是为了保证自己写博客的完善性，我决定还是放出来，算是有一段结束，再进行新的开始。
二、LADRC离散实现
直接进入正题，因为是一年半以前写的了，过程和期间考虑的也忘记了，这次仅仅做一个总结，不能太保证准确性，同时自己工作重心也不想放这上面了（Xin Lei），但是框架和方向肯定是没错的。选择一个简单的对象进行实验，对于一个传递函数，
G
(
s
)
=
1
s
2
+
2
s
+
4
(1)
G(s) = frac{1}{s^2+2s+4} tag{1}
G(s)=s2+2s+41(1)
采样时间选择0.001s，因此得到z变换的传递函数为，
G
(
z
)
=
4.997
∗
1
0
−
7
z
+
4.993
∗
1
0
−
7
z
2
−
1.998
z
+
0.998
(2)
G(z) = frac{4.997*10^{-7}z+4.993*10^{-7}}{z^2-1.998z+0.998} tag{2}
G(z)=z2−1.998z+0.9984.997∗10−7z+4.993∗10−7(2)
接下来基于LADRC的框架进行离散化，其中LESO部分离散化为，
%% 包含了初始化部分和迭代部分
% 初始化部分
z1 = zeros(1, len);
z2 = zeros(1, len);
z3 = zeros(1, len);
% Future z(i-1) now z(i-2) before z(i-3)
z1(2) = z1(1) + sampleTime*(3*omega_o*(y(3) - z1(1)) + z2(1));
z2(2) = z2(1) + sampleTime*(3*omega_o^2*(y(3) - z1(1)) + b0*u(2) + z3(1));
z3(2) = z3(1) + sampleTime*(omega_o^3*(y(3) - z1(1)));
%% 迭代部分
for i = 1:len-1
% Future z(i-1) now z(i-2) before z(i-3)
z1(i+2) = z1(i+1) + sampleTime*(3*omega_o*(y(i+3) - z1(i+1)) + z2(i+1));
z2(i+2) = z2(i+1) + sampleTime*(3*omega_o^2*(y(i+3) - z1(i+1)) + b0*u(i+2) + z3(i+1));
z3(i+2) = z3(i+1) + sampleTime*(omega_o^3*(y(i+3) - z1(i+1)));
z1(i+1) = z1(i+2);
z2(i+1) = z2(i+2);
z3(i+1) = z3(i+2);
end
PD控制器部分，
%% 初始化部分
% y(k) = -1.998*y(k-1) - 0.998*y(k-2) + 4.997e-7*u(k) + 4.993e-7*u(k - 1)
y = zeros(1, len);
u = zeros(1, len);
% Initialize all
e1(1) = input_signal(1) - z1(1);
u0(1) = Kp*e1(1) - Kd*z2(1);
e2(1) = u0(1) - z3(1);
u(1) = 0;
u(2) = e2(1) / b0;
% G(s) = 1/(s^2 + 2*s + 4);
% Gz = c2d(G, sampleTime) -----> Y/U = (4.997e-07 z + 4.993e-07) / (z^2 - 1.998 z + 0.998)
y(3) = 1.998*y(2) - 0.998*y(1) + 4.997e-7*u(2) + 4.993e-7*u(1);
error = 0;
%% 迭代部分
e1(i+1) = input_signal(i+1) - z1(i+1);
u0(i+1) = Kp*e1(i+1) - Kd*z2(i+1);
e2(i+1) = u0(i+1) - z3(i+1);
error = error + abs(e1(i+1));
u(i+2) = e2(i+1) / b0;
% G(s) = 1/(s^2 + 2*s + 4);
% Gz = c2d(G, sampleTime) -----> Y/U = (4.997e-07 z + 4.993e-07) / (z^2 - 1.998 z + 0.998)
y(i+3) = 1.998*y(i+2) - 0.998*y(i+1) + 4.997e-7*u(i+2) + 4.993e-7*u(i+1);
y(i+1) = y(i+2);
y(i+2) = y(i+3);
u(i+1) = u(i+2);
LADRC整体结构构建程序
% step 1: transfer function descrete.
% step 2: assemble all
clear
clc
%% Set sample time and end time, note: shanno sampling theory
sampleTime = 0.001;
offset = 0;
% 1.0
endtime = 1.5;
len = endtime / sampleTime;
t = sampleTime:sampleTime:endtime;
%% Parameter
%%% 0.019 15 180
%%% 0.05 15 90
b0 = 0.019; % bo greater than or equal to b
omega_c = 15;
omega_o = 187.6250;
b0 = 0.019; % bo greater than or equal to b
omega_c = 20;
omega_o = 187;
Kp = omega_c.^2;
Kd = 2*omega_c;
%% Set input signal
switch(1)
case 1
stepTime = 0.1;
Temp = stepTime / sampleTime;
input_signal(1:Temp) = 0;
input_signal(Temp:len+1) = 1;
case 2
input_signal = impluse();
case 3
input_signal = wave();
case 4
input_signal = userDefine();
end
%% Descrete transfer function
% G(s) = 1/(s^2 + 2*s + 4);
% Gz = c2d(G, sampleTime) -----> Y/U = (4.997e-07 z + 4.993e-07) / (z^2 - 1.998 z + 0.998)
% Z^(-1) ---> y(k+2) - 1.998*y(k+1) + 0.998*y(k) = 4.997e-7*u(k+1) + 4.993e-7*u(k)
% ---> y(k) = 1.998*y(k-1) - 0.998*y(k-2) + 4.997e-7*u(k-1) + 4.993e-7*u(k-2)
%% Initialize all
u0 = zeros(1, len);
z1 = zeros(1, len);
z2 = zeros(1, len);
z3 = zeros(1, len);
e1 = zeros(1, len);
e2 = zeros(1, len);
% Up to Gp(s) transfer function.
% y(k) = -1.998*y(k-1) - 0.998*y(k-2) + 4.997e-7*u(k) + 4.993e-7*u(k - 1)
y = zeros(1, len);
u = zeros(1, len);
%% Initialize all
e1(1) = input_signal(1) - z1(1);
u0(1) = Kp*e1(1) - Kd*z2(1);
e2(1) = u0(1) - z3(1);
u(1) = 0;
u(2) = e2(1) / b0;
% G(s) = 1/(s^2 + 2*s + 4);
% Gz = c2d(G, sampleTime) -----> Y/U = (4.997e-07 z + 4.993e-07) / (z^2 - 1.998 z + 0.998)
y(3) = 1.998*y(2) - 0.998*y(1) + 4.997e-7*u(2) + 4.993e-7*u(1);
% Future z(i-1) now z(i-2) before z(i-3)
z1(2) = z1(1) + sampleTime*(3*omega_o*(y(3) - z1(1)) + z2(1));
z2(2) = z2(1) + sampleTime*(3*omega_o^2*(y(3) - z1(1)) + b0*u(2) + z3(1));
z3(2) = z3(1) + sampleTime*(omega_o^3*(y(3) - z1(1)));
error = 0;
%% Pro proccessing and update
for i = 1:len-1
e1(i+1) = input_signal(i+1) - z1(i+1);
u0(i+1) = Kp*e1(i+1) - Kd*z2(i+1);
e2(i+1) = u0(i+1) - z3(i+1);
error = error + abs(e1(i+1));
u(i+2) = e2(i+1) / b0;
% G(s) = 1/(s^2 + 2*s + 4);
% Gz = c2d(G, sampleTime) -----> Y/U = (4.997e-07 z + 4.993e-07) / (z^2 - 1.998 z + 0.998)
y(i+3) = 1.998*y(i+2) - 0.998*y(i+1) + 4.997e-7*u(i+2) + 4.993e-7*u(i+1);
% Future z(i-1) now z(i-2) before z(i-3)
z1(i+2) = z1(i+1) + sampleTime*(3*omega_o*(y(i+3) - z1(i+1)) + z2(i+1));
z2(i+2) = z2(i+1) + sampleTime*(3*omega_o^2*(y(i+3) - z1(i+1)) + b0*u(i+2) + z3(i+1));
z3(i+2) = z3(i+1) + sampleTime*(omega_o^3*(y(i+3) - z1(i+1)));
y(i+1) = y(i+2);
y(i+2) = y(i+3);
z1(i+1) = z1(i+2);
z2(i+1) = z2(i+2);
z3(i+1) = z3(i+2);
u(i+1) = u(i+2);
end
error = error / length(u);
% input_signal = input_signal(1:len);
% u = u(1:len);
% y = y(1:len);
% z1 = z1(1:len);
% z2 = z2(1:len);
% z3 = z3(1:len);
%%
subplot(311)
plot(t, input_signal(1:len), t, y(1:len), t, z1(1:len),'--');
xlabel('Time array');
ylabel('set and y');
legend('set', 'y', 'z1')
subplot(312)
plot(t, z2(1:len))
xlabel('Time array');
ylabel('z2 Value');
legend('z2');
subplot(313)
plot(t, z3(1:len))
xlabel('Time array');
ylabel('z3 Value');
legend('z3');
三、结果
其中LADRC参数选择为
b
0
=
0.019
,
ω
c
=
15
,
ω
o
=
187.6250
b_0=0.019,omega_c=15,omega_o=187.6250
b0=0.019,ωc=15,ωo=187.6250,最后运行结果如下，
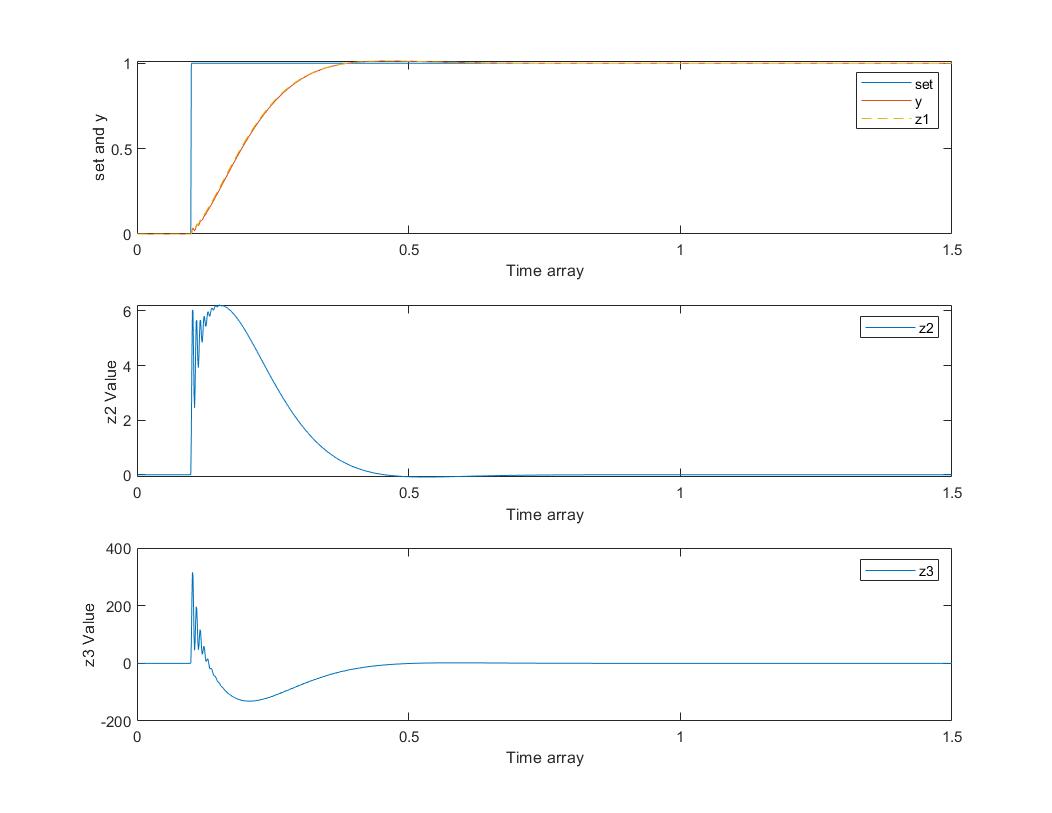
这里第一幅图为响应曲线，第二个为LESO估计的y的导数，第三个为LESO估计的总扰动。
四、总结
通过离散化以后发现，在Matlab中使用Simulink仿真实际上是被优化过的，在现实应用中，LADRC受到了采样时间和噪声的约束。希望以后有机会能在工程中真的应用一下检测它的极限在哪些地方。
最后
以上就是欣慰皮带为你收集整理的LADRC的离散化实现（Mark一下，重新开始）的全部内容，希望文章能够帮你解决LADRC的离散化实现（Mark一下，重新开始）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复