预备知识
根据合式公式的真值表与主合取范式与主析取范式的关系来求。在命题逻辑中,合式公式的真值表的应用非常广泛。列合式公式真值表的步骤如下:
- 找出合式公式中出现的所有命题变项。
- 按照二进制的顺序给出命题公式的2n种赋值。
- 对每个赋值按照合式公式的层次求出它的值。
- 所有成真赋值的合取即为主合取范式,所有成假赋值的析取即为主析取范式
熟悉真值表定义,并列出合式公式的真值表,并根据真值表的结果来判断公式的类型。
源程序参考
PropostionalLogicHeader头文件
/**************************************************************************
* (C) Copyright 2015-2018 by Gavin Y. Liu All Rights Reserved. *
* *
* DISCLAIMER: The authors and publisher shall not be liable in any event *
* for incidental or consequential damages in connection with, or arising *
* out of, the furnishing, performance, or use of these programs. *
**************************************************************************/
/* File: PropostionalLogicHeader.h
*-------------------------------
* This interface exports a simple symboll table abstraction
*
*/
#ifndef _PROPOSTIONALLOGICHEADER_H_
#define _PROPOSTIONALLOGICHEADER_H_
/*
* Constants
*------------------
* LengthMaxLimit - Length Max value for the tables
*/
#define LengthMaxLimit 100
/*Private function prototypes*/
/*
* Function: negation
* Usage: negation(p);
*-------------------
* This funtion is an operation that takes a proposition p to another proposition "not p",
* written ¬p, which is interpreted intuitively as being true when p is false and false when p is true.
*/
static int negation(const int p);
/*
* Function: conjunction
* Usage: conjunction(p,q);
* ---------------------------------
* This function is an operation on two logical values, typically the values of two propositions, that
* produces a value of true if and only if both of its operands are true.The conjunctive identity is 1,
* which is to say that AND-ing an expression with 1 will never change the value of the expression. In
* keeping with the concept of vacuous truth, when conjunction is defined as an operator or function of
* arbitrary arity, the empty conjunction (AND-ing over an empty set of operands) is often defined as
* having the result 1.
*/
static int conjunction(const int p,const int q);
/*
* Function: disjunction
* Usage: disjunction(p,q);
*----------------------------------------
* The Function is the values of two propositions, that has a value of false if and only if both of its
* operands are false. More generally, a disjunction is a logical formula that can have one or more literals
* separated only by ORs. A single literal is often considered to be a degenerate disjunction.
*
* The disjunctive identity is false, which is to say that the or of an expression with false has the same
* value as the original expression. In keeping with the concept of vacuous truth, when disjunction is defined
* as an operator or function of arbitrary arity, the empty disjunction (OR-ing over an empty set of operands)
* is generally defined as false.
*/
static int disjunction(const int p, const int q);
/*
* Function: conditional
* Usage: conditional(p,q)
* ----------------------------------------
* The function is The material conditional is used to form statements of the form "p→q" (termed a conditional
* statement) which is read as "if p then q" and conventionally compared to the English construction "If...
* then...". But unlike as the English construction may, the conditional statement "p→q" does not specify a
* causal relationship between p and q and is to be understood to mean "if p is true, then q is also true" such
* that the statement "p→q" is false only when p is true and q is false.[1] The material conditional is also to
* be distinguished from logical consequence.
*/
static int conditional(const int p, const int q);
/*
* Function:bicondtional
* Usage: bincontional(p,q)
* ----------------------------------------------
* The function is the logical connective of two statements asserting "p if and only if q", where q is an
* antecedent and p is a consequent. This is often abbreviated p iff q. The operator is denoted using a
* doubleheaded arrow (↔), a prefixed E (Epq), an equality sign (=), an equivalence sign (≡), or EQV. It is
* logically equivalent to (p → q) ∧ (q → p), or the XNOR (exclusive nor) boolean operator. It is equivalent to
* "(not p or q) and (not q or p)". It is also logically equivalent to "(p and q) or (not p and not q)", meaning
* "both or neither".
*
* The only difference from material conditional is the case when the hypothesis is false but the conclusion is
* true. In that case, in the conditional, the result is true, yet in the biconditional the result is false.
*
* In the conceptual interpretation, a = b means "All a 's are b 's and all b 's are a 's"; in other words, the
* sets a and b coincide: they are identical. This does not mean that the concepts have the same meaning.
* Examples: "triangle" and "trilateral", "equiangular trilateral" and "equilateral triangle". The antecedent is
* the subject and the consequent is the predicate of a universal affirmative proposition.
*
* In the propositional interpretation, a ⇔ b means that a implies b and b implies a; in other words, that the
* propositions are equivalent, that is to say, either true or false at the same time. This does not mean that
* they have the same meaning. Example: "The triangle ABC has two equal sides", and "The triangle ABC has two
* equal angles". The antecedent is the premise or the cause and the consequent is the consequence. When an
* implication is translated by a hypothetical (or conditional) judgment the antecedent is called the hypothesis
* (or the condition) and the consequent is called the thesis.
*/
static int biconditional(const int p, const int q);
/*
* Function:compute
* Usage: compute(p,q ch)
* ----------------------------------
*/
static int compute(const int p, const int q, const char ch);
/*
* Function: is_proposition
* Usage: is_propositon(ch)
* ----------------------------------
*/
static int is_proposition(const char ch);
/*
* Function:is_LogicalConnectives
* Usage: is_LogicalConnectives(c)
* ----------------------------------
*/
static int is_LogicalConnectives(const char c);
/*
* Function:get_isp
* Usage: get_isp(ch)
* ----------------------------------
*/
static int get_isp(const char ch);
/*
* Function:get_icp
* Usage: get_icp(ch)
* ----------------------------------
*/
static int get_icp(const char ch);
/*
* Function:to_InersePolandT
* Usage: to_InersePolandT(*last_exp, *pre_exp)
* -------------------------------------------
*/
static void to_InversePolandT(char *last_exp, const char *pre_exp);
/*
* Function: add_blackets
* Usage: add_blackets(s)
* ----------------------------
*/
static void add_blackets(char* s);
/*
* Function: exp_resolve
* Usage: exp_resolve(*exp,length,(*re_exp)[LengMaxLimit],k)
* ----------------------------
*/
static void exp_resolve(const char* exp, const int length, char (*re_exp)[LengthMaxLimit] , int k);
static void binary_inc(int* a, int length);
/*
* Function: get_proposition
* Usage: get_proposition(*exp,length,*p)
* ------------------------------------------
* The propositions in these logics are more complex. First, terms must be defined. A term is (i) a variable or
* (ii) a function symbol applied to the number of terms required by the function symbol's arity. For example,
* if + is a binary function symbol and x, y, and z are variables, then x+(y+z) is a term, which might be written
* with the symbols in various orders. A proposition is (i) a predicate symbol applied to the number of terms
* required by its arity, (ii) an operator applied to the number of propositions required by its arity, or
* (iii) a quantifier applied to a proposition. For example, if = is a binary predicate symbol and ∀ is a
* quantifier, then ∀x,y,z [(x = y) → (x+z = y+z)] is a proposition. This more complex structure of propositions
* allows these logics to make finer distinctions between inferences, i.e., to have greater expressive power.
*
* In this context, propositions are also called sentences, statements, statement forms, formulas, and well-formed
* formulas, though these terms are usually not synonymous within a single text. This definition treats propositions
* as syntactic objects, as opposed to semantic or mental objects. That is, propositions in this sense are meaningless,
* formal, abstract objects. They are assigned meaning and truth-values by mappings called interpretations and
* valuations, respectively.
*/
static int get_proposition(const char* exp, const int length, char* p);
static void proposition_ass(const char* pre_exp, int length, char *p, int* v, int n, char* last_exp);
static int bin2dec(int* v, int n);
/* Public function prototyes*/
/*
* Function:is_wellformed
* Usage:is_wellformed(s,length)
* -----------------------------------
* The formulas are inductively defined as follows:
* Each propositional variable is, on its own, a formula.
* If φ is a formula, then lnotφ is a formula.
* If φ and ψ are formulas, and • is any binary connective, then ( φ • ψ) is a formula.
* Here • could be (but is not limited to) the usual operators ∨, ∧, →, or ↔.
* This definition can also be written as a formal grammar in Backus–Naur form, provided the set
* of variables is finite.
*/
int is_wellformed(const char *s,const int length);
/*
* Function: compute_wellformed
* Usage: compute_wellformed(exp,length)
* -------------------------------------------
*/
int compute_wellformed(const char* exp, const int length);
/*
* Function: truth_table
* Usage: truth_table(exp,length)
* ----------------------------------
* a truth table is composed of one column for each input variable (for example, A and B), and
* one final column for all of the possible results of the logical operation that the table is
* meant to represent (for example, A XOR B). Each row of the truth table therefore contains one
* possible configuration of the input variables (for instance, A=true B=false), and the result of
* the operation for those values. See the examples below for further clarification.
*/
void truth_table(const char* exp, const int length);
int get_main_disjunction(const char* exp, char* resu);
int get_main_conjunction( char* exp, char* resu);
void help();
#endif // end of _PROPOSTIONALLOGICHEADER_H_PropostionalLogicSource源文件
/**************************************************************************
* (C) Copyright 2015-2018 by Gavin Y. Liu All Rights Reserved. *
* *
* DISCLAIMER: The authors and publisher shall not be liable in any event *
* for incidental or consequential damages in connection with, or arising *
* out of, the furnishing, performance, or use of these programs. *
**************************************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#include <string.h>
#include <math.h>
#include "PropostionalLogicHeader.h"
/*Private functions */
//Compute testing
static int compute(const int p, const int q, const char ch){
switch(ch){
case '~':
return negation(q);
case '+':
return disjunction(p, q);
case '*':
return conjunction(p, q);
case '>':
return conditional(p, q);
case '=':
return biconditional(p, q);
default:
return -1;
}
}
//Negation
static int negation(const int p){
return p == 0 ? 1 : 0;
}
//Conjunction
static int conjunction(const int p, const int q){
return (p != 0 && q != 0) ? 1 : 0;
}
//Disjunction
static int disjunction(const int p, const int q){
return (p == 0 && q == 0) ? 0 : 1;
}
//Conditional
static int conditional(const int p, const int q){
return (p != 0 && q == 0) ? 0 : 1;
}
//Biconditional
static int biconditional(const int p, const int q){
return ((p == 0 && q == 0) || (p != 0 && q != 0)) ? 1 : 0;
}
//Whether or not is Propostion?
static int is_proposition(const char ch){
return isalpha(ch) || isalnum(ch);
}
//Whether or not is Logical Connnectives?
static int is_LogicalConnectives(const char c){
switch(c){
case '+':
case '*':
case '>':
case '~':
case '=':
return 1;
default:
return 0;
}
}
//Stack Priority
static int get_isp(const char ch){
switch(ch){
case '#':
return 0;
case '+':
case '*':
case '=':
case '>':
return 5;
case '~':
return 7;
case '(':
return 1;
case ')':
return 8;
default:
return -1;
}
}
//Stack Priority
static int get_icp(const char ch){
switch(ch)
{
case '#':
return 0;
case '+':
case '*':
case '=':
case '>':
return 4;
case '~':
return 6;
case '(':
return 8;
case ')':
return 1;
default:
return -1;
}
}
//Inverse Poland Type
static void to_InversePolandT(char* last_exp, const char* pre_exp){
char sign_stack[LengthMaxLimit] = {'�'};
int sp = -1;
int pp = 0;
int lp = 0;
sign_stack[++sp] = '#';
while(pre_exp[pp] != '�'){
if(is_proposition(pre_exp[pp])) {
last_exp[lp++] = pre_exp[pp];
}
else{
while(get_icp(pre_exp[pp]) < get_isp(sign_stack[sp])){
last_exp[lp++] = sign_stack[sp];
sign_stack[sp--] = '�';
}
if(get_icp(pre_exp[pp]) == get_isp(sign_stack[sp]))
sign_stack[sp--] = '�';
else
sign_stack[++sp] = pre_exp[pp];
}
pp++;
}
while(sp != 0){
last_exp[lp++] = sign_stack[sp--];
}
}
static void add_blackets(char* s){
int len = strlen(s);
memcpy(s + 1, s, len);
s[0] = '(';
s[len + 1] = ')';
}
static void exp_resolve(const char* exp, const int length, char (*re_exp)[LengthMaxLimit] , int k){
char stack[LengthMaxLimit][LengthMaxLimit] = {"�"};
char rpn_exp[LengthMaxLimit] = "�";
char tmp_exp[LengthMaxLimit] = "�";
int sp = -1;
int len = 0;
int i = 0;
int j = 0;
to_InversePolandT(rpn_exp, exp);
for(i = 0; i < length; i++){
if(j > k){
break;
}
else if(rpn_exp[i] == '~'){
memset(tmp_exp, '�', sizeof(char) * LengthMaxLimit);
strncpy(tmp_exp, &rpn_exp[i], sizeof(char));
strcpy(tmp_exp + strlen(tmp_exp), stack[sp]);
add_blackets(tmp_exp);
memset(stack[sp], '�', sizeof(char) * LengthMaxLimit);
sp--;
strcpy(stack[++sp], tmp_exp);
j++;
}
else if(is_LogicalConnectives(rpn_exp[i])){
memset(tmp_exp, '�', sizeof(char) * LengthMaxLimit);
strcpy(tmp_exp, stack[sp-1]);
strncpy(tmp_exp + strlen(tmp_exp), &rpn_exp[i], 1);
strcpy(tmp_exp + strlen(tmp_exp), stack[sp]);
add_blackets(tmp_exp);
memset(stack[sp], '�', sizeof(char) * LengthMaxLimit);
memset(stack[sp - 1], '�', sizeof(char) *LengthMaxLimit);
sp -= 2;
strcpy(stack[++sp], tmp_exp);
j++;
}
else if(is_proposition(rpn_exp[i])){
strncpy(stack[++sp], &rpn_exp[i], 1);
}
}
strcpy(re_exp[k], tmp_exp);
}
static void binary_inc(int* a, int length){
int i = 0, c = 0;
a[length - 1] += 1;
for(i = length - 1; i > 0; i--) {
if(a[i] > 1){
a[i] = 0;
a[i - 1] += 1;
}
else
break;
}
}
static int get_proposition(const char* exp, const int length, char* p){
int i = 0;
int j = 0;
int k = 0;
int n = 0;
for(i = 0; i < length; i++){
if(is_proposition(exp[i])){
j = 0;
k = 0;
while(p[j] != '�') {
if(exp[i] == p[j]){
k = 1;
break;
}
j++;
}
if(k == 0){
p[j] = exp[i];
n++;
}
}
}
return n;
}
static void proposition_ass(const char* pre_exp, int length, char *p, int* v, int n, char* last_exp)
{
int j = 0, k = 0;
for(j = 0; j < length; j++) {
if(is_proposition(pre_exp[j])){
for(k = 0; k < n; k++){
if(pre_exp[j] == p[k])
last_exp[j] = v[k] + '0';
}
}
else
last_exp[j] = pre_exp[j];
}
}
//Binary to Dec
static int bin2dec(int* v, int n)
{
int num = 0, i = 0;
for(i = n - 1; i > -1; i--)
{
if(v[i] == 0)
continue;
num += (int)pow(2.0, n - i - 1);
}
return num;
}
/*Public functions */
// Compute for well formed formula Values
int compute_wellformed(const char* exp, const int length)
{
if(!is_wellformed(exp, length)){
printf("The expression is not a well formedn");
return -1;
}
char last_exp[LengthMaxLimit] = {'�'};
int stack[LengthMaxLimit] = {0};
int lp = 0, sp = -1, r, i;
for(i = 0; i < length; i++){
if(isalpha(exp[i])){
printf("does not assigment");
return -1;
}
}
to_InversePolandT(last_exp, exp);
while(last_exp[lp] != '�')
{
if(isalnum(last_exp[lp])){
stack[++sp] = last_exp[lp] - '0';
}
else if(last_exp[lp] == '~'){
r = compute(0, stack[sp--], last_exp[lp]);
stack[++sp] = r;
}
else if(is_LogicalConnectives(last_exp[lp])){
r = compute(stack[sp-1], stack[sp], last_exp[lp]);
sp -= 2;
stack[++sp] = r;
}
lp++;
}
return stack[sp];
}
//Whether or not is well-formed?
int is_wellformed(const char* s, const int length){
int l_bracket = 0;
int r_bracket = 0;
int i = 0;
if(length == 1 && is_proposition(s[i]))
return 1;
while(i < length){
if(is_proposition(s[i])){
if(!is_LogicalConnectives(s[i + 1]) && s[i + 1] != ')' && s[i + 1] != '�' || s[i + 1] == '~')
return 0;
}
else if(is_LogicalConnectives(s[i])){
if(!is_proposition(s[i + 1]) && s[i + 1] != '~' && s[i + 1] != '(')
return 0;
}
else if(s[i] == '(')
{
if(s[i + 1] != '~' && !is_proposition(s[i + 1]) && s[i + 1] != '(')
return 0;
l_bracket++;
}
else if(s[i] == ')')
{
if(s[i + 1] != '�' && !is_LogicalConnectives(s[i + 1]) && s[i + 1] != ')' || s[i + 1] == '~')
return 0;
r_bracket++;
}
i++;
}
if(l_bracket == r_bracket)
return 1;
else
return 0;
}
//print truth table
void truth_table(const char* exp, const int length)
{
if(!is_wellformed(exp, length)) {
printf("The expression is not a wffn");
return;
}
int i, j, k, r, n = 0, m = 0;
char s[LengthMaxLimit] = "�";
char p[LengthMaxLimit] = "�";
char ss[LengthMaxLimit][LengthMaxLimit] = {'�'};
n = get_proposition(exp, length, p);
m = (int)pow(2.0, n);
int* v = new int[m];
memset(v, 0, sizeof(int) * m);
memset(ss, '�', sizeof(char) * LengthMaxLimit * LengthMaxLimit);
for(i = 0, k = 0; i < length; i++){
if(is_LogicalConnectives(exp[i])){
exp_resolve(exp, length, ss, k);
k++;
}
}
for(j = 0; j < n; j++)
printf("%c ", p[j]);//print propostional
for(j = 0; j < k; j++)
printf("%s ", ss[j]);
printf("n");
for(i = 0; i < m; i++){
for(j = 0; j < n; j++)
printf("%d ", v[j]);
for(j = 0; j < k; j++){
memset(s, '�', sizeof(char) * LengthMaxLimit);
proposition_ass(ss[j], strlen(ss[j]), p, v, n, s);
r = compute_wellformed(s, strlen(s));
printf("%d ", r);
}
binary_inc(v, n);
printf("n");
}
delete[] v;
}
//Main Disjunction
int get_main_disjunction(const char* exp, char* resu)
{
int len = strlen(exp);
if(!is_wellformed(exp, len))
return 0;
memset(resu, '�', sizeof(char) * LengthMaxLimit);
char tmp_exp[LengthMaxLimit] = "�";
char p[LengthMaxLimit] = "�";
int i = 0, r = 0;
int n = get_proposition(exp, len, p);
int m = (int)pow(2.0, n);
int* v = new int[m];
memset(v, 0, sizeof(int) * m);
int r_index = 0;
for(i = 0; i < m; i++)
{
proposition_ass(exp, len, p, v, n, tmp_exp);
r = compute_wellformed(tmp_exp, strlen(tmp_exp)); //compute to well-fomred
if(r == 1)
{
if(r_index - 1 > -1 && resu[r_index - 1] != '�')
resu[r_index++] = '+';
char strn[10] = "�", num = 0;
num = bin2dec(v, n);
resu[r_index++] = 'm';
_itoa(num, strn, 10);
memcpy(resu + r_index, strn, sizeof(char) * strlen(strn));
resu += strlen(strn); //以上几行为添加范式
}
binary_inc(v, n);
}
delete[] v;
return 1;
}
//Main conjunction
int get_main_conjunction( char* exp, char* resu)
{
int len = strlen(exp);
if(!is_wellformed(exp, len))
return 0;
memset(resu, '�', sizeof(char) *LengthMaxLimit);
char tmp_exp[LengthMaxLimit] = "�";
char p[LengthMaxLimit] = "�";
int i = 0, r = 0;
int n = get_proposition(exp, len, p);
int m = (int)pow(2.0, n);
int* v = new int[m];
memset(v, 0, sizeof(int) * m);
int r_index = 0;
for(i = 0; i < m; i++)
{
proposition_ass(exp, len, p, v, n, tmp_exp);
r = compute_wellformed(tmp_exp, strlen(tmp_exp));
if(r == 0)
{
if(r_index - 1 > -1 && resu[r_index - 1] != '�')
resu[r_index++] = '*';
char strn[10] = "�", num = 0;
num = bin2dec(v, n);
resu[r_index++] = 'M';
_itoa(num, strn, 10);
memcpy(resu + r_index, strn, sizeof(char) * strlen(strn));
resu += strlen(strn);
}
binary_inc(v, n);
}
delete[] v;
return 1;
}
void help(){
printf("*********************************************************");
printf("n*ttttttt*");
printf("n*tt Welcome to Propostion Settt*");
printf("n*ttttttt*");
printf("n*t Usage:tttttt*");
printf("n*tt'~': Negationtttt*");
printf("n*tt'+': Disjunctionttt*");
printf("n*tt'*': Conjunctionttt*");
printf("n*tt'>': Conditionalttt*");
printf("n*tt'=': Biconditionalttt*");
printf("n*tt'default': -1tttt*");
printf("n*ttttttt*");
printf("n*********************************************************");
printf("n");
} Main源文件
/**************************************************************************
* (C) Copyright 2015-2018 by Gavin Y. Liu All Rights Reserved. *
* *
* DISCLAIMER: The authors and publisher shall not be liable in any event *
* for incidental or consequential damages in connection with, or arising *
* out of, the furnishing, performance, or use of these programs. *
**************************************************************************/
#include <stdio.h>
#include <string.h>
#include "PropostionalLogicHeader.h"
/*main program */
int main( ){
help();
char s[100];
int length, r = 0;
while(scanf("%s", s) && s[0] != '#'){
length = strlen(s);
printf("expression is: %snn", s);
//Whether or not is well-formed?
printf("is_wellformed Formula? %dnn", is_wellformed(s, length));
printf("compute_wellfomred is: ");
r = compute_wellformed(s, length);
if(r > -1)
printf("%d", r);
printf("nn");
printf("Print True tablen");
truth_table(s,length);
char dis_form[LengthMaxLimit];
get_main_disjunction(s, dis_form);
printf("main disjunction normal form is: %snn", dis_form);
char con_form[LengthMaxLimit];
get_main_conjunction(s, con_form);
printf("main conjunction normal form is: %snn", con_form);
}
return 0;
}测试结果
界面

测试:p蕴含q,然后蕴含r

测试: p析取q,然后蕴含r
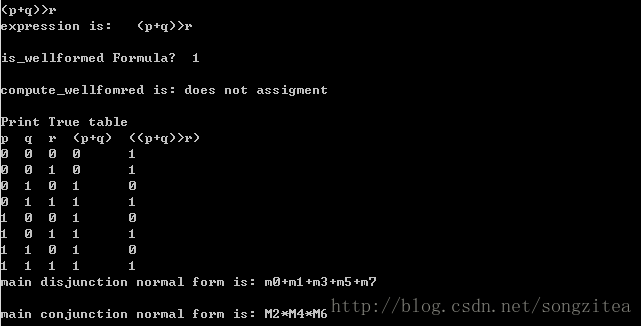
测试:p蕴含q,然后析取r

关于Discrete Mathematics更多讨论与交流,敬请关注本博客和新浪微博songzi_tea.
最后
以上就是眼睛大飞机最近收集整理的关于离散数学实践:真值表与范式的全部内容,更多相关离散数学实践内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复