一、数制与码制
1、数制
1.1、十进制(Decimal)
- 有0~9,10个数码。
- 逢十进一。
- 基数为十
( N ) D = ∑ i = − m n − 1 d i 1 0 i (N)_D = sum_{i = -m}^{n-1} d_i10^i (N)D=i=−m∑n−1di10i
1.2、二进制(Binary)
- 有0、1,2个数码。
- 逢二进一。
- 基数为二
( N ) B = ∑ i = − m n − 1 b i 2 i (N)_B = sum_{i = -m}^{n-1} b_i2^i (N)B=i=−m∑n−1bi2i
1.2.1、八进制(Octal)
实际为三位二进制数
1.2.2、十六进制(Hexadecimal)
实际为四位二进制数
1.3、任意进制
- 有0~(R-1),R个数码。
- 逢R进一。
- 基数为R
( N ) R = ∑ i = − m n − 1 r i r i (N)_R = sum_{i = -m}^{n-1} r_ir^i (N)R=i=−m∑n−1riri
2、码制
2.1、原码反码和补码
2.1.1正数
符号位为0,且原码反码和补码一致
[+45]原 = 00101101
[+45]反 = 00101101
[+45]补 = 00101101
2.1.2负数
符号位为0
[-45]原 = 10101101
反码在原码的基础上,除符号位外,均取反
[-45]反 = 11010010
补码在反码的基础上,加一
[-45]补 = 11010011
补码10000为什么表示-16?
前提条件是,数字位数,是6位二进制数.
范围是:00 0000~11 1111,最大值是:31.模,就是:32,即 100 0000.
在6位二进制数条件下,-16 的原码、反码,都不存在,求反加一,是不能用的.
补码,有个定义式,一般的书上,都有的.简化如下:
[X]补 = X ; X 为零和正数
[X]补 = 模 - |X| ; X 为负数
按定义式来计算,[-16]补 = 32 - |-16| = 16 = 10 0000(二进制)
按照定义式求补码,这才是补码的详细原理.
求反加一,只不过是一个简便做法,并不是原理.
补码原理,并没有进制的限制,即,任何进制,都可以求出补码.
而求反加一,只能用于二进制.
以求反加一为重点的书,层次较低,很难能说明补码的原理.
2.1.3减法运算
- 8 - 8 = 8 + (-8) = 0
(8 - 8)补 = 8补 + (-8补) = 00000100 +11111100 = 0补 = 0原
- 21- 26 = 21 + (-26) = -5
(21- 26)补 = 21补 + (-26)补 = 00010101补 + 11100110补 = 11111011补
(21- 26)原 = 10000101 = -5
2.2、二进制编码
2.2.1、BCD码(Binary-Coded Decimal)
BCD码(Binary-Coded Decimal),用4位二进制数来表示1位十进制数中的0~9这10个数码,是一种二进制的数字编码形式,用二进制编码的十进制代码。
| 十进制数 | 8421码 | 5421码 | 2421码 | 余3码 | 余3循环码 |
|---|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0011 | 0010 |
| 1 | 0001 | 0001 | 0001 | 0100 | 0110 |
| 2 | 0010 | 0010 | 0010 | 0101 | 0111 |
| 3 | 0011 | 0011 | 0011 | 0110 | 0101 |
| 4 | 0100 | 0100 | 0100 | 0111 | 0100 |
| 5 | 0101 | 1000 | 1011 | 1000 | 1100 |
| 6 | 0110 | 1001 | 1100 | 1001 | 1101 |
| 7 | 0111 | 1010 | 1101 | 1010 | 1111 |
| 8 | 1000 | 1011 | 1110 | 1011 | 1110 |
| 9 | 1001 | 1100 | 1111 | 1100 | 1010 |
- 8421
8421 BCD码是最基本和最常用的BCD码,它和四位自然二进制码相似,各位的权值为8、4、2、1,故称为有权BCD码。和四位自然二进制码不同的是,它只选用了四位二进制码中前10组代码,即用0000~1001分别代表它所对应的十进制数,余下的六组代码不用。
- 5421和2421
5421 BCD码和2421 BCD码为有权BCD码,它们从高位到低位的权值分别为5、4、2、1和2、4、2、1。这两种有权BCD码中,有的十进制数码存在两种加权方法,例如,5421 BCD码中的数码5,既可以用1000表示,也可以用0101表示;2421 BCD码中的数码6,既可以用1100表示, 也可以用0110表示。这说明5421 BCD码和2421 BCD码的编码方案都不是惟一的,表1-2只列出了一种编码方案。
上表中2421 BCD码的10个数码中,0和9、1和8、2和7、3和6、4和5的代码对应位恰好一个是0时,另一个就是1。就称0和9、1和8互为反码。
- 余3 码
余3码是8421 BCD码的每个码组加3(0011)形成的。常用于BCD码的运算电路中。
- 余3循环码
余3循环码是无权码,即每个编码中的1和0没有确切的权值,整个编码直接代表一个数值。主要优点是相邻编码只有一位变化,避免了过渡码产生的“噪声”。
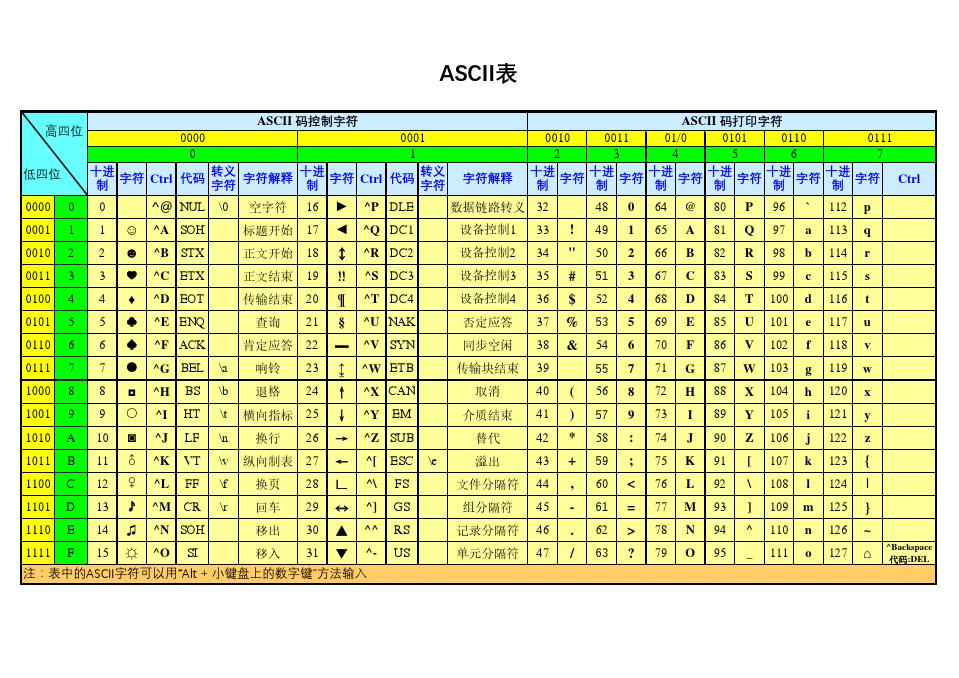
2.2.2、ASCII码(美国信息交换标准代码)
二、逻辑代数基本运算
1、三种最基本的逻辑运算和门电路
逻辑代数有与、或、非三种基本逻辑运算。du它是按一定的逻辑关系进行运算的代数,zhi是用来分析和设计数字电路的dao数学工具。
1.1与逻辑(与门)
-
逻辑关系:有0则0,全1才1
-
逻辑表达式:
Y = A ⋅ B Y = A cdot B Y=A⋅B -
逻辑符号
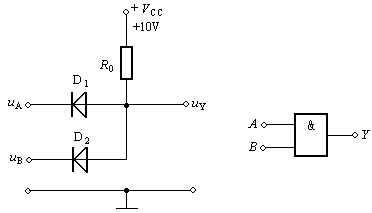
1.1或逻辑(与门)
-
逻辑关系:有1则1,全0才0
-
逻辑表达式:
Y = A + B Y = A + B Y=A+B -
逻辑符号
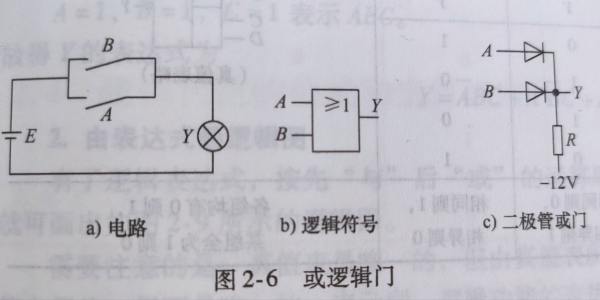
1.1非逻辑(非门)
-
逻辑关系:1则0,0则1
-
逻辑表达式:
Y = A ‾ Y = overline A Y=A -
逻辑符号
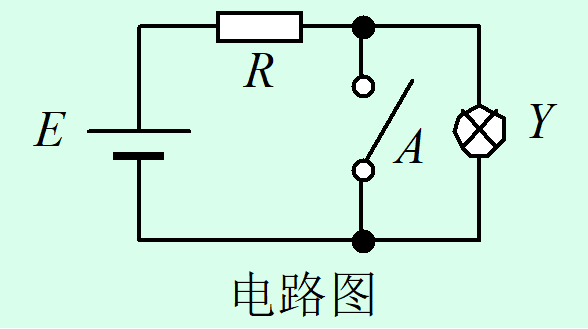
最后
以上就是沉默啤酒最近收集整理的关于第一周:数字逻辑基础一、数制与码制二、逻辑代数基本运算的全部内容,更多相关第一周内容请搜索靠谱客的其他文章。








发表评论 取消回复