???? 前言:21世纪是信息数字化的时代,“数字逻辑设计”是数字技术的基础,是电子、计算机类各专业的主要技术基础课程之一。从天上到陆地,从陆地到海洋。大到卫星,小到玩具。全世界正在经历一场由0和1数字编码来表达和传输信息的一场革命。

目录
- ???? 1. 数字信号
- ???? 1.1 概念
- ???? 1.2 表示方法
- ???? 2. 进制及其转换
- ???? 2.1 二进制与十进制之间的转换
- ???? 2.2 二进制与十六进制之间的转换
- ???? 2.3 二进制与八进制之间的转换
- ???? 3. 二-十进制代码(BCD码)
- ???? 3.1 常见的BCD码
- ???? 3.1.1 有权BCD码
- ???? 3.1.2 无权BCD码
- ???? 4. 算术运算与逻辑运算
- ???? 5. 数字电路
???? 1. 数字信号
???? 1.1 概念
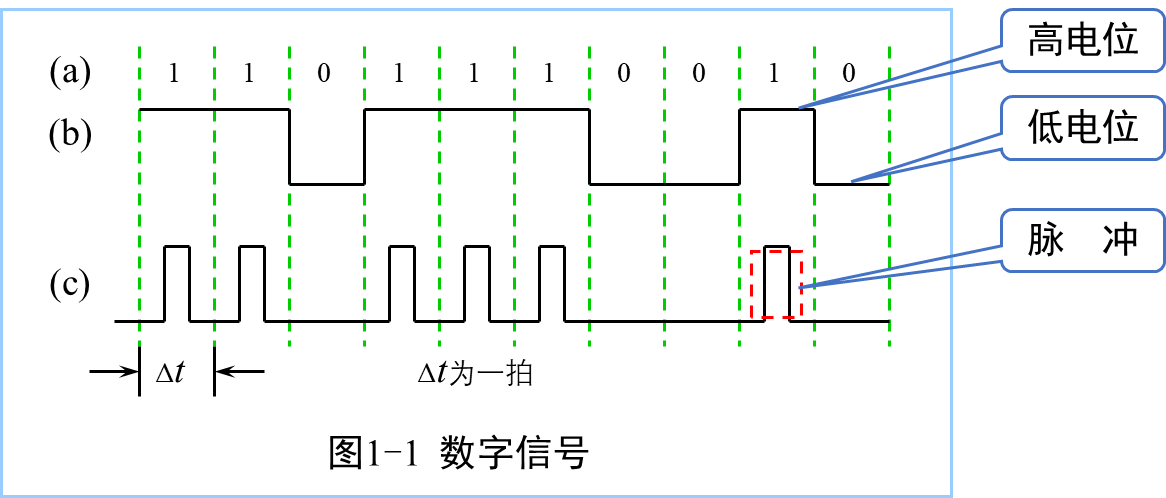
- 在时间上和数量上都不连续,变化总是发生在一系列离散的瞬间,数量大小和每次的增减变化都是某一个最小单位的整数倍,这一类物理量叫做数字量。表示数字量的信号称为数字信号。工作在数字信号下的电路叫做数字电路。
- 数字电路中采用只有0、1两种数值组成的数字信号。
- 模拟信号在时间上和数值上都具有连续变化的特点。在某一瞬间的值可以是一个数值区间内的任何值。
???? 1.2 表示方法
???? 2. 进制及其转换
数制:指进位计数制,即用进位的方法来计数,数制包括计数符号(数码)和进位规则两个方面。
常用数制有十进制、十二进制、十六进制、八进制等。
我们以十进制举例:
(1)计数符号: 0,1,2,3,4,5,6,7,8,9
(2)进位规则:逢十进一;
(3)十进制数按权展开式:
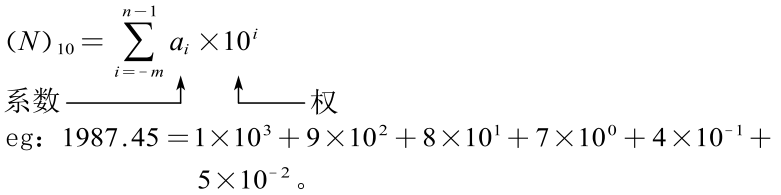
???? 2.1 二进制与十进制之间的转换
- 二进制数转换为十进制数(
按权展开法)
例1:

注:该方法同样适用八进制、十六进制等转为二进制。 - 十进制数转换为二进制数
-
方法一:提取2的幂法:
例2:
( 45.5 ) 10 = 32 + 8 + 4 + 1 + 0.5 (45.5)_{10}=32+8+4+1+0.5 (45.5)10=32+8+4+1+0.5
= 1 × 2 5 + 0 × 2 4 + 1 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 + 1 × 2 − 1 =1 times 2^{5}+0 times 2^{4}+1 times 2^{3}+1 times 2^{2}+0 times 2^{1}+1 times 2^{0}+1 times 2^{-1} =1×25+0×24+1×23+1×22+0×21+1×20+1×2−1
= ( 101101.1 ) 2 =(101101.1)_{2} text { } =(101101.1)2 -
方法二(推荐):
除二取余法、乘二取整法
例3:: ( 75.625 ) 10 = ( ) 2 (75.625)_{10}=( )_2 (75.625)10=()2
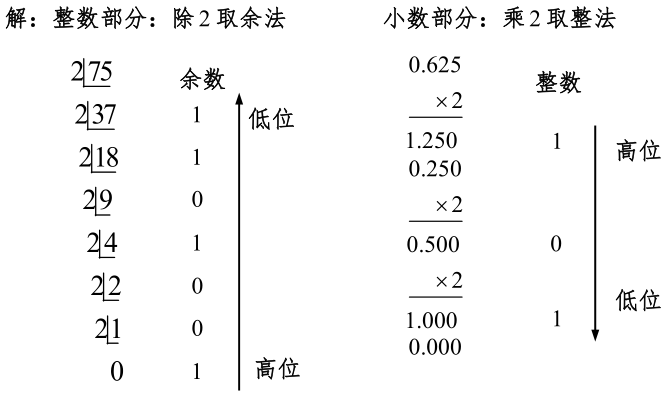
答案: ( 75.625 ) 10 = ( 1001011.101 ) 2 (75.625)_{10}=(1001011.101)_2 (75.625)10=(1001011.101)2
注:小数部分保留4位。此外,该方法同样适用转为八进制、十六进制等。
???? 2.2 二进制与十六进制之间的转换
-
二进制转十六进制
例4: ( 101010.110 ) 2 = ( ) 16 (101010.110)_2 = ( )_{16} (101010.110)2=( )16
解: |0010|1010.|1100|高位补0
2 A . C
答案:2AC -
十六进制转二进制
例5: ( 7 A . 3 ) 16 = ( ) 2 (7A.3)_{16} = ( )_2 (7A.3)16=( )2
解: 7 A . 3
0111 1010. 0011
答案:0111 1010.0011
???? 2.3 二进制与八进制之间的转换
-
二进制转八进制
例6: ( 11011.11 ) 2 = ( ) 8 (11011.11)_2 = ( )_8 (11011.11)2=( )8
解: |011|011.|110|高位补0
3 3 .6
答案:33.6 -
八进制转二进制
例7: ( 63.2 ) 8 = ( ) 2 (63.2)_8 = ( )_2 (63.2)8=( )2
解: 6 3 . 2
110 011 . 010
答案:110 011.010
???? 3. 二-十进制代码(BCD码)
以二进制码表示一个十进制数的代码,称为二-十进制码,即BCD(Binary Code Decimal)码。
利用 4 位二进制码表示一位十进制数,也就是只能表示0-9,常用的是 8421 BCD 码,其与自然二进制码相似。
-
十进制转BCD
例8: ( 639.7 ) 10 = ( ) 8421 B C D (639.7)_{10} = ( )_{8421BCD} (639.7)10=( )8421BCD
解: 6 3 9. 7
0110 0011. 1001. 0111
答案:0110 0011 1001.0111 -
BCD转十进制
例9: ( 1000 1001 0011. 0111 1001 ) 8421 B C D = ( ) 10 (1000 1001 0011. 0111 1001)_{8421BCD} = ( )_{10} (1000 1001 0011. 0111 1001)8421BCD=( )10
解: |1000|1001|0011.|0111|1001|高位补0
8 9 3. 7 9
答案:893.79
???? 3.1 常见的BCD码
十进制 数码 8421 码 余3码 2421 码 5121 码 631 − 1 码 单位间距码 (格雷码) 余3 循环码 移存码 0 0000 0011 0000 0000 0011 0000 0010 0001 1 0001 0100 0001 0001 0010 0001 0110 0010 2 0010 0101 0010 0010 0101 0011 0111 0100 3 0011 0110 0011 0011 0111 0010 0101 1001 4 0100 0111 0100 0111 0110 0110 0100 0011 5 0101 1000 1011 1000 1001 0111 1100 0111 6 0110 1001 1100 1100 1000 0101 1101 1111 7 0111 1010 1101 1101 1010 0100 1111 1110 8 1000 1011 1110 1110 1101 1100 1110 1100 9 1001 1100 1111 1111 1100 1101 1010 1000 begin{array}{c|c|c|c|c|c|c|c|c} hline begin{array}{c} text { 十进制 } \ text { 数码 } end{array} & 8421 text { 码 } & text { 余3码 } & 2421 text { 码 } & 5121 text { 码 } & 631-1 text { 码 } & begin{array}{c} text { 单位间距码 } \ text { (格雷码) } end{array} & begin{array}{c} text { 余3 } \ text { 循环码 } end{array} & text { 移存码 } \ hline 0 & 0000 & 0011 & 0000 & 0000 & 0011 & 0000 & 0010 & 0001 \ hline 1 & 0001 & 0100 & 0001 & 0001 & 0010 & 0001 & 0110 & 0010 \ hline 2 & 0010 & 0101 & 0010 & 0010 & 0101 & 0011 & 0111 & 0100 \ hline 3 & 0011 & 0110 & 0011 & 0011 & 0111 & 0010 & 0101 & 1001 \ hline 4 & 0100 & 0111 & 0100 & 0111 & 0110 & 0110 & 0100 & 0011 \ hline 5 & 0101 & 1000 & 1011 & 1000 & 1001 & 0111 & 1100 & 0111 \ hline 6 & 0110 & 1001 & 1100 & 1100 & 1000 & 0101 & 1101 & 1111 \ hline 7 & 0111 & 1010 & 1101 & 1101 & 1010 & 0100 & 1111 & 1110 \ hline 8 & 1000 & 1011 & 1110 & 1110 & 1101 & 1100 & 1110 & 1100 \ hline 9 & 1001 & 1100 & 1111 & 1111 & 1100 & 1101 & 1010 & 1000 \ hline end{array} 十进制 数码 01234567898421 码 0000000100100011010001010110011110001001 余3码 00110100010101100111100010011010101111002421 码 00000001001000110100101111001101111011115121 码 0000000100100011011110001100110111101111631−1 码 0011001001010111011010011000101011011100 单位间距码 (格雷码) 0000000100110010011001110101010011001101 余3 循环码 0010011001110101010011001101111111101010 移存码 0001001001001001001101111111111011001000
???? 3.1.1 有权BCD码
每位数码都有确定的位权的码。例如: 8421码、 5421码、2421码(如 5421码1011 代表5+0+2+1=8 , 2421码1100 代表2+4+0+0=6)
(1) 8421码和代表0-9的二进制数一一对应;
(2) 5421码的前5个码和8421码相同,后5个码在前5个码的基础上加1000构成,这样的码前5个码和后5个码一一对应,仅高位不同;
(3) 2421码前5个码和8421码相同,后5个码以中心对称取反,这样的码称为自反代码,如: 4→0100 , 5→1011 , 0→0000 , 9→1111 。
???? 3.1.2 无权BCD码
即代码没有确定的位权值,不能按照位权展开求解所代表的十进制数。如表1-3中的余3码、单位间距码、余3循环码等。这些代码都有其特点,适用于不同的场合。(余3码的编码规律为:在8421码上加0011 , 6的余3码为:0110+0011=1001)
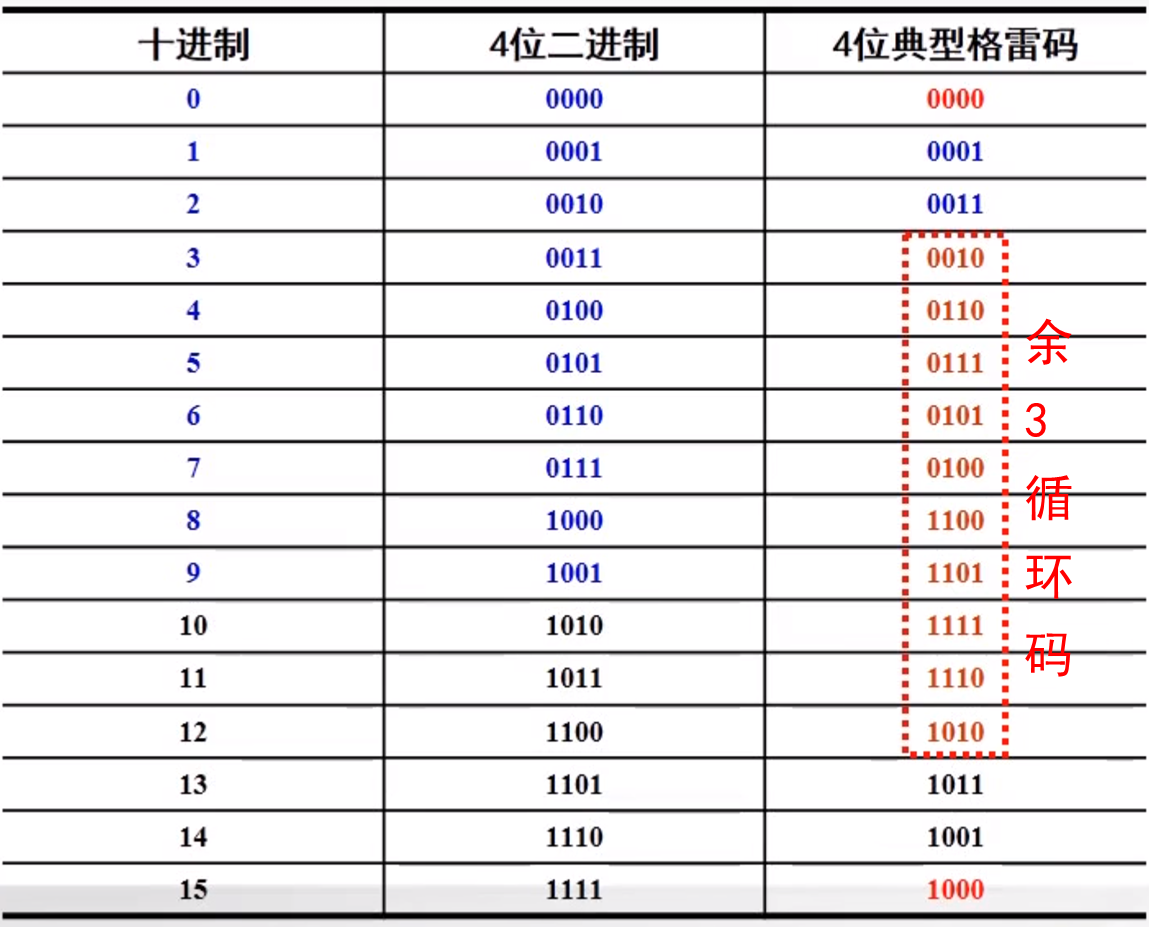
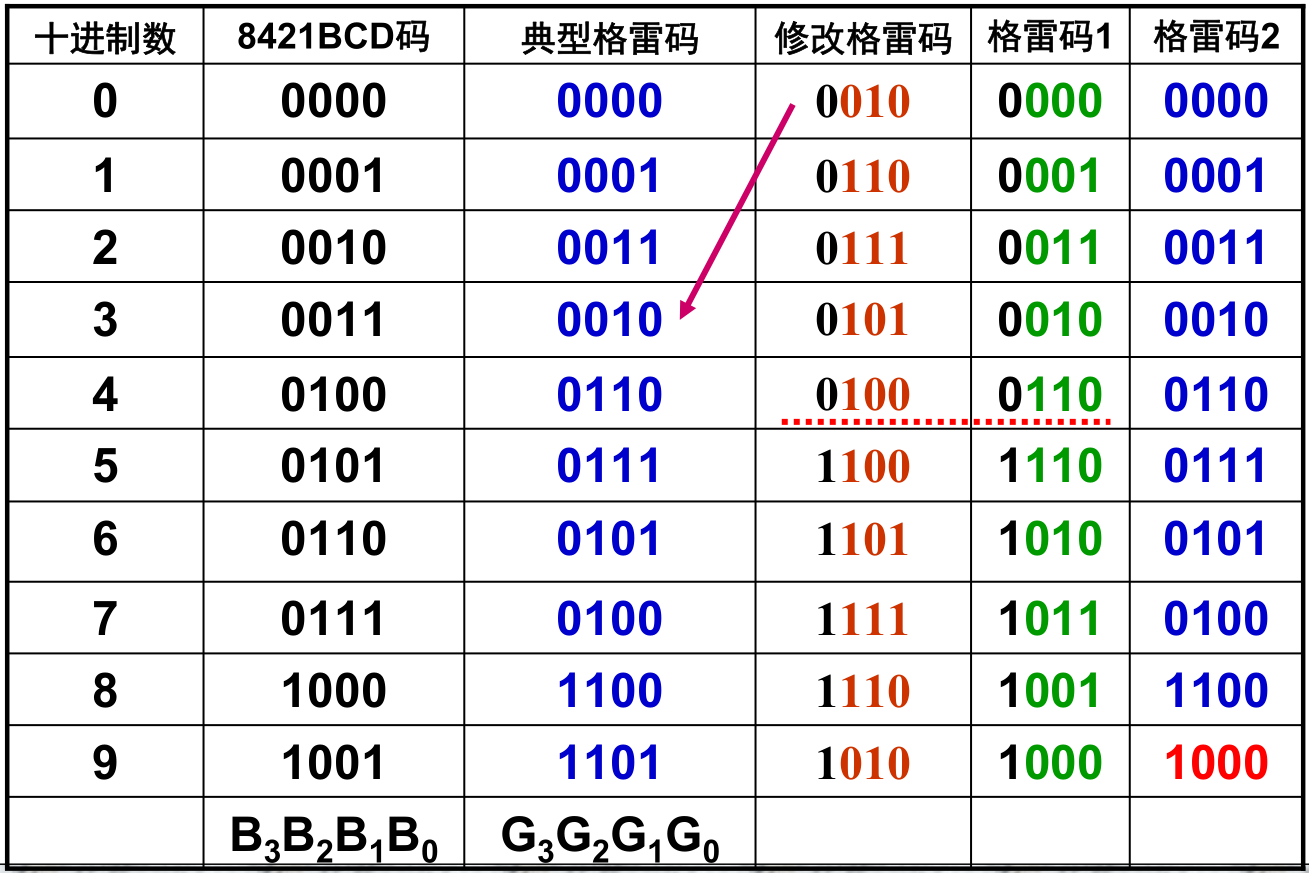
格雷码是一种 无权码 ,其特点是任意两个相邻码组之间只有一位码元不同。典型的n位格雷码中,0和最大数(2n-1)之间也只有一位码元不同。因此它是一种循环码。
与普通二进制码相比,格雷码在传输过程中引起的误差较小,因为相邻码组中仅有一位码元不同,这样可减小逻辑上的差错,避免可能存在的瞬间模糊状态,所以它是错误最小化代码。
典型格雷码与8421码关系简单,即 G i = B i + 1 ⊕ B i G_i = B_{i+1} oplus B_i Gi=Bi+1⊕Bi
???? 4. 算术运算与逻辑运算
- 当两个二进制数码表示数量大小时,它们之间可以进行数值运算,称这种运算为算术运算。二进制数的算术运算法则和十进制数的运算法则基本相同,只是相邻两位之间的关系是“逢二进一”及“借一当二”。
- 1 位二进制数码0和1,还可表示两种不同的状态,即数字电路中的逻辑状态。此时,二进制数码0和1之间将按照某种逻辑关系进行逻辑运算。
???? 5. 数字电路
对数字信号进行算术运算和逻辑运算的电路称为数字电路。将众多的数字电路基本单元制作在一块半导体基片上,称为集成电路。
集成电路 包含基本元件的数目 小规模集成电路(SSIC) 10 ∼ 100 中规模集成电路 (MSIC) 100 ∼ 1000 大规模集成电路 (LSIC) 1000 ∼ 10000 超大规模集成电路 (VLSIC) 10000 以上 begin{array}{c|c} hline text { 集成电路 } & text { 包含基本元件的数目 } \ hline text { 小规模集成电路(SSIC) } & 10 sim 100 \ hline text { 中规模集成电路 (MSIC) } & 100 sim 1000 \ hline text { 大规模集成电路 (LSIC) } & {1 0 0 0} sim {1 0 0 0 0} \ hline text { 超大规模集成电路 (VLSIC) } & {1 0 0 0 0} text { 以上 } \ hline end{array} 集成电路 小规模集成电路(SSIC) 中规模集成电路 (MSIC) 大规模集成电路 (LSIC) 超大规模集成电路 (VLSIC) 包含基本元件的数目 10∼100100∼10001000∼1000010000 以上
OK,以上就是本期知识点“绪论”的知识啦~~ ,感谢友友们的阅读。后续还会继续更新,欢迎持续关注哟????~
????如果有错误❌,欢迎批评指正呀????~让我们一起相互进步????
????如果觉得收获满满,可以点点赞????支持一下哟~
最后
以上就是要减肥过客最近收集整理的关于【数字逻辑】——绪论(学习笔记)???? 1. 数字信号???? 2. 进制及其转换???? 3. 二-十进制代码(BCD码)???? 4. 算术运算与逻辑运算???? 5. 数字电路的全部内容,更多相关【数字逻辑】——绪论(学习笔记)????内容请搜索靠谱客的其他文章。








发表评论 取消回复