Codeforces 981 C. Useful Decomposition [思维]

107 阅读 0 评论 71 点赞

我是靠谱客的博主跳跃白开水，最近开发中收集的这篇文章主要介绍Codeforces 981 C. Useful Decomposition [思维]，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Ramesses knows a lot about problems involving trees (undirected connected graphs without cycles)!

He created a new useful tree decomposition, but he does not know how to construct it, so he asked you for help!

The decomposition is the splitting the edges of the tree in some simple paths in such a way that each two paths have at least one common vertex. Each edge of the tree should be in exactly one path.

Help Remesses, find such a decomposition of the tree or derermine that there is no such decomposition.

Input

The first line contains a single integer $n n$ ( $2 \leq n \leq 10^{5} 2\leqn\leq105$ ) the number of nodes in the tree.

Each of the next $n - 1 n - 1$ lines contains two integers $a_{i} ai$ and $b_{i} bi$ ( $1 \leq a_{i}, b_{i} \leq n 1\leqai,bi\leqn$ , $a_{i} \neq b_{i} ai\neqbi$ ) — the edges of the tree. It is guaranteed that the given edges form a tree.

Output

If there are no decompositions, print the only line containing "No".

Otherwise in the first line print "Yes", and in the second line print the number of paths in the decomposition $m m$ .

Each of the next $m m$ lines should contain two integers $u_{i} ui$ , $v_{i} vi$ ( $1 \leq u_{i}, v_{i} \leq n 1\lequi,vi\leqn$ , $u_{i} \neq v_{i} ui\neqvi$ ) denoting that one of the paths in the decomposition is the simple path between nodes $u_{i} ui$ and $v_{i} vi$ .

Each pair of paths in the decomposition should have at least one common vertex, and each edge of the tree should be presented in exactly one path. You can print the paths and the ends of each path in arbitrary order.

If there are multiple decompositions, print any.

Examples

input

Copy
4
1 2
2 3
3 4

output

Copy
Yes
1
1 4

input

Copy
6
1 2
2 3
3 4
2 5
3 6

output

Copy
No

input

Copy
5
1 2
1 3
1 4
1 5

output

Copy
Yes
4
1 2
1 3
1 4
1 5

Note

The tree from the first example is shown on the picture below: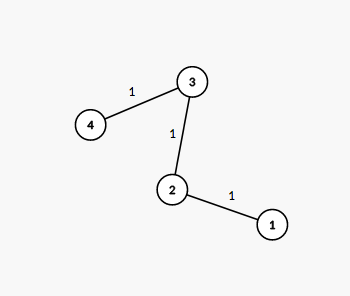 $\text{[math]}$ The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.

The tree from the second example is shown on the picture below: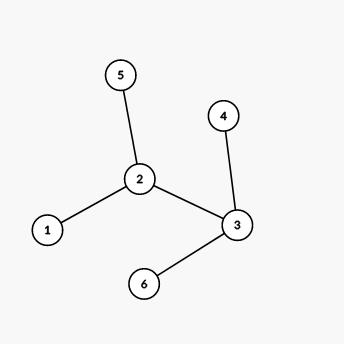 $\text{[math]}$ We can show that there are no valid decompositions of this tree.

The tree from the third example is shown on the picture below: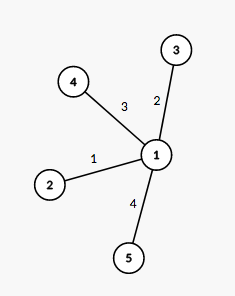 $\text{[math]}$

The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.

题目：给定一棵树，要求拆成若干条简单路径，并且这些路径都经过一个公共节点。给出任意一个解决方案，如不存在输出No。

分析：所有简单路径都经过一个公共节点，我们倒推回去，就是把公共节点看成根节点，然后从这个节点出发，没有分叉的节点;

那么只要先判断分叉节点是不是唯一的，如果唯一，那么把所有路径拆下来就可以啦！！！

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5+7;
int cnt[maxn], endv[maxn], n, tot;
int main()
{
//freopen("in.txt", "r", stdin);
while(~scanf("%d", &n))
{
tot = 0;
for(int i = 0; i < n - 1; i++)
{
int a, b;
scanf("%d%d", &a,&b);
cnt[a]++;
cnt[b]++;
}
int aim = -1;
bool f = true;
for(int i = 1; i <= n; i++){
if(cnt[i] >= 3)
{
if(aim == -1) aim = i;
else {
puts("No");
f = false;
break;
}
}
if(cnt[i] == 1) endv[tot++] = i;
}
if(!f) continue;
puts("Yes");
if(aim == -1) printf("1n%d %dn", endv[0], endv[1]);
else {
printf("%dn", tot);
for(int i = 0; i < tot; i++)
printf("%d %dn", aim, endv[i]);
}
}
return 0;
}