11.17菜鸡的日常

状态极差，感觉遇到了问题。。。。

牛客练习赛的B题:

题目描述

第一行两个数n和m
第二行n-1个数，第i个数fa[i + 1]表示i + 1点的父亲编号，保证fa[i + 1]<i + 1
第三行m个数，每个数x依次表示这次操作的点是x

输出一个数，即这m次操作的答案的hash值
如果是第i次操作，这次操作结果为ans,则这个hash值加上
i * ans
输出hash值对19260817取模的结果

题解;

考虑每次修改的贡献
 
对于每个节点x维护几个标记：
tag[x]:x被操作的次数
anstag[x]:从子树贡献上来的贡献
sontag[x]:x的儿子被操作的总次数
修改的时候：
首先anstag[x] += deg[x]+1
然后对父亲：anstag[ fa[x] ] += 2
然后对父亲的父亲：anstag[ fa[ fa[x] ]++
然后x被操作了一次，所以tag[x]++
然后x作为fa[x]的儿子，有：sontag[ fa[x] ]++
查询的时候：
首先ans = anstag[x]
然后x的父亲每次操作对x有2的贡献：
所以ans += tag[ fa[x] ] * 2
x的父亲的父亲每次操作对x有1的贡献：
所以ans += tag[ fa[ fa[x] ] ]
再考虑到x的父亲的其他儿子对于x的贡献：
ans += sontag[ fa[x] ] - tag[x]
因为要去掉x自己的值
这样维护就可以了
总复杂度O( n + m )

#include <bits/stdc++.h>
namespace fastIO {
#define BUF_SIZE 6000000
// fread -> read
bool IOerror = 0;
char nc() {
static char buf[BUF_SIZE], *pl = buf + BUF_SIZE, *pr = buf + BUF_SIZE;
if(pl == pr) {
pl = buf;
pr = buf + fread(buf, 1, BUF_SIZE, stdin);
if(pr == pl) {
IOerror = 1;
return -1;
}
}
return *pl++;
}
inline bool blank(char ch) {
return ch == ' ' || ch == 'n' || ch == 'r' || ch == 't';
}
void read(int &x) {
char ch;
while(blank(ch = nc()));
if(IOerror)
return;
for(x = ch - '0'; (ch = nc()) >= '0' && ch <= '9'; x = x * 10 + ch - '0');
}
#undef BUF_SIZE
};
using namespace fastIO;
using namespace std;
const int N = 1E5 + 7, mod = 19260817;
typedef long long ll;
int tag[N], sontag[N], f[N], sz[N];
ll sonans[N];
int main()
{
int n, m, x;
read(n),read(m);
for(int i = 2;i <= n;i ++) {
read(f[i]);
sz[i] ++;
sz[f[i]] += sz[i];
}
ll hash = 0;
for(ll i = 1;i <= m;i ++) {
read(x);
ll ans = 0;
sonans[x] += sz[x] + 1;
sonans[f[x]] += 2;
sonans[f[f[x]]] ++;
tag[x] ++;
sontag[f[x]] ++;
ans = sonans[x];
ans += tag[f[x]] * 2 + tag[f[f[x]]];
ans += sontag[f[x]] - tag[x];
hash = hash + i * ans;
if(hash >= mod) hash %= mod;
}
printf("%lldn",hash);
return 0;
}

题目描述

第一行三个数n,x,y
之后一行n个数表示a序列
之后一行n个数表示b序列

一行一个非负数表示答案

10 0 233333
227849 218610 5732 128584 21857 183426 199367 211615 91725 110029
8064826 14174520 10263202 9863592 592727 7376631 5733314 1062933 12458325 15046167

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2E5 + 7;
ll a[N],b[N];
int main()
{
std::ios::sync_with_stdio(false), cin.tie(0);
ll n, x, y;
cin >> n >> x >> y;
for(int i = 1;i <= n;i ++) cin >> a[i];
for(int i = 1;i <= n;i ++) cin >> b[i];
sort(a+1, a+n+1);
sort(b+1, b+n+1);
for(int i = 1;i <= n;i ++) {
if(y <= a[i] || x == 0) break;
if(a[i] < b[i] && y > a[i]) {
a[i] = y, x--;
}
}
sort(a+1,a+1+n);
ll ans = 0;
for(int i = 1;i <= n;i ++) {
if(a[i] >= b[i]) continue;
ans = max(ans, b[i]-a[i]);
}
cout << ans << endl;
return 0;
}


Codeforces:892D - Gluttony

题意:


D. Gluttony



time limit per test
2 seconds



memory limit per test
256 megabytes



input
standard input



output
standard output



You are given an array a with n distinct integers. Construct an array b by permuting a such that for every non-empty subset of indices S = {x1, x2, ..., xk} (1 ≤ xi ≤ n, 0 < k < n) the sums of elements on that positions in a and b are different, i. e.






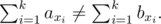Input

The first line contains one integer n (1 ≤ n ≤ 22) — the size of the array.
The second line contains n space-separated distinct integers a1, a2, ..., an (0 ≤ ai ≤ 109) — the elements of the array.



Output

If there is no such array b, print -1.
Otherwise in the only line print n space-separated integers b1, b2, ..., bn. Note that b must be a permutation of a.
If there are multiple answers, print any of them.

题解：因为N个不同的数，所以先离散化(为了便于理解)排序,然后每个第k大数都变为原来的k+1大，a[n-1]变为a[0],这样就保证了新数组里除非全取不然不可能子集会先相等，

证明:

原序列:a[0],a[1],a[2],............a[n-1]

新序列:b[0],b[1],b[2].............b[n-1]

令差序列为c

c[1] = b[1]-a[1],c[2] = b[2]-a[2], c[n-1]=b[n-1]-a[n-1]

假设下标k对应为a数组里最大的元素,则仅有b[k] < a[k],其他因为某个都变大都有b[k] > a[k],又因为c[1]+c[2]+...c[n]=0,所以要想平衡这个关系必须全取，所以其子集一定不会平衡，不会相等。

最后

以上就是默默战斗机为你收集整理的11.17菜鸡的日常的全部内容，希望文章能够帮你解决11.17菜鸡的日常所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。