概述
2020-03-23
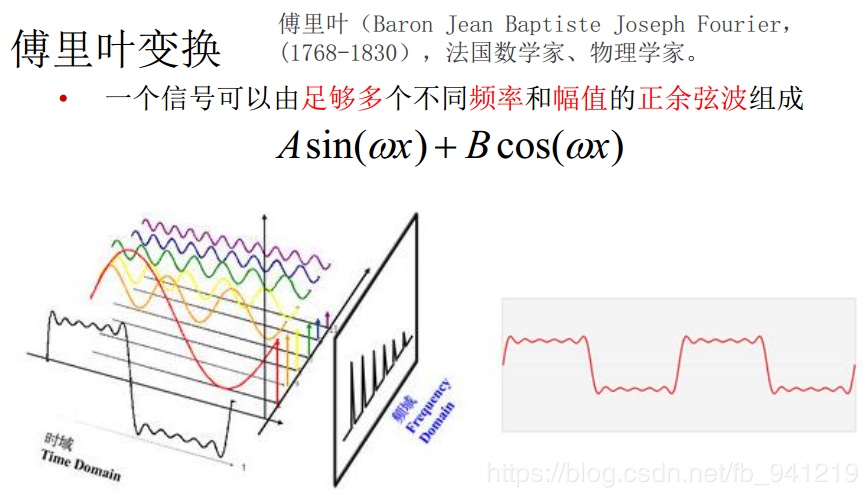
傅立叶级数是将周期函数表示成由多个 (或无穷多个) 不同频率的正弦函数和余弦函数的线性组合，这些不同的频率是不连续的，例如傅立叶级数：
其 sin 内的 x, 3x, 5x 是不连续的。而傅立叶积分是将傅立叶级数延伸到非周期函数，但这些不同的频率是连续的，例如：若 f(x) 的傅立叶积分=
周期函数
(1). 若函数 f(x) 的定义域为实数集合 R 且存在一正数 T，使得 f(x+T)=f(x)，x∈R，则称 f(x) 为周期函数，且此正的数值 T 称为 f(x) 的周期。
(2). 若 f(x) 和 g(x) 的周期均为 T，则 h(x)=af(x)±bg(x) 亦为周期 T 的函数。
(3). 若 f(x) 的周期为 T，则 f(kx) 的周期为：
(4). 若 f(x) 的周期为 mT，g(x) 的周期为 nT，则 h(x)=af(x)±bg(x) 的周期为 m, n 的最小公倍数乘以 T。(若 m, n 为分数，则先通分后再取分子的最小公倍数)
(5). 常数函数 f(x)=c，亦为周期函数，其周期为任意数。
(6). 级数
，其中
(7). 三角级数的周期为 2π。
(ex.47) 求 sin(2x)+cos(3x) 的周期。
Sol：
(1) . sin(2x) 的周期为
(2) . cos(3x) 的周期为
周期为 2π 的傅立叶级数
(1). 若函数 f(x) 是周期为 2π 的周期函数，则其可以用下面的三角级数表示：
(2). 在上式中，若 f(x) 已知，则
pf：略
(3). 用法：要求周期为 2π 的周期函数 f(x) 的傅立叶级数时，
(a). 抄下
(b). 抄下
(c). 将题目的 f(x) 代入 (b) 式。
(d). 将 (b) 式积分出来，求出
(e). 重复 (b)~(d) 式，算出
(f). 最后将
(g).
(4). 若
(ex.48) 求 f(x) 的周期为 2π，且
Sol：由傅立叶级数公式知
(1).
(2).
(3).
偶函数与奇函数的傅立叶级数
此节的目的是要简化计算傅立叶系数的过程。
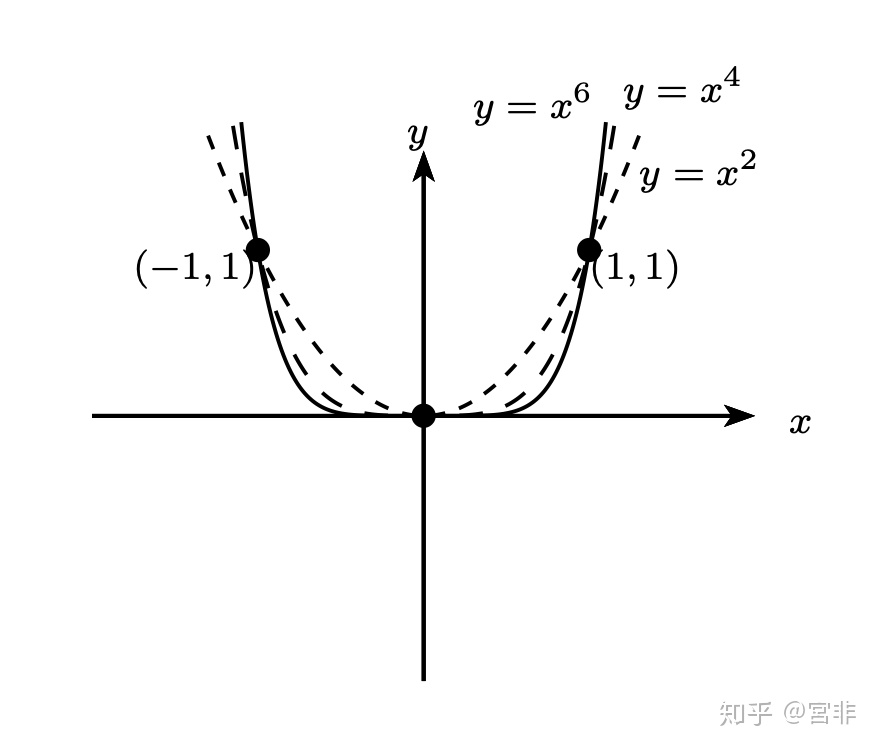
(1). 若函数 f(x) 满足 f(-x)=f(x)，则 f(x) 称为偶函数，例如：
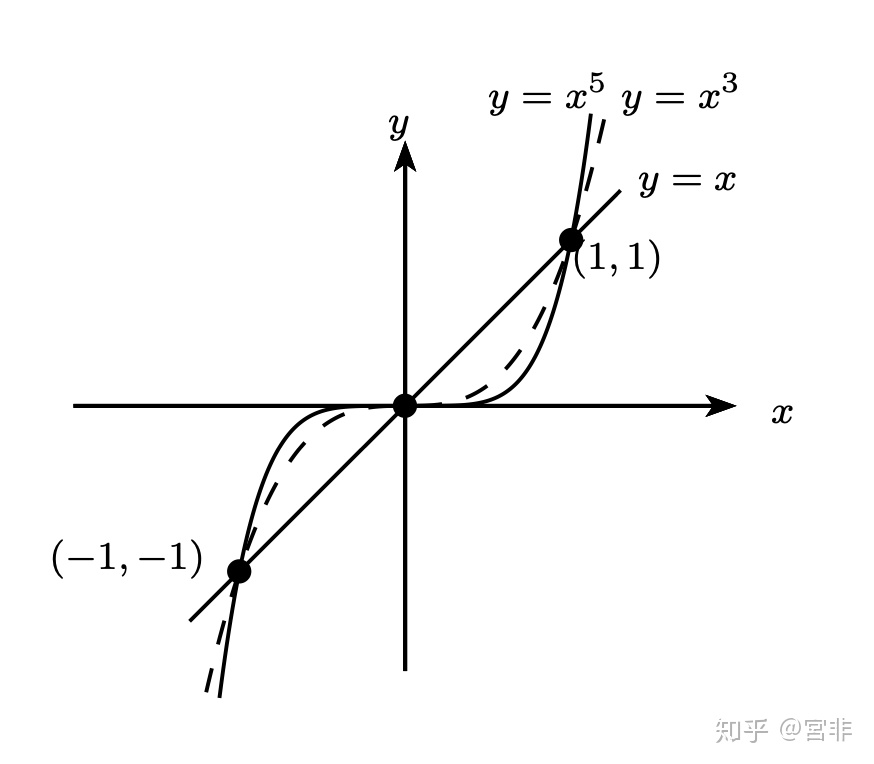
(2). 若函数 g(x) 满足 g(-x)=-g(x)，则 g(x) 称为奇函数，例如：
(3). 偶函数与偶函数的乘积为偶函数，例如：
(4). 偶函数积分积一个周期等于积半个周期的 2 倍，即若函数 f(x) 是周期为 2π 的偶函数，
(5). 奇函数积分积一个周期的值为 0，即若函数 g(x) 是周期为 2π 的奇函数，则
(6). 若函数 f(x) 是周期为 2π 的周期函数，且为偶函数，则 f(x) 和 f(x)cosnx 为偶函数，f(x)sinnx 为奇函数，所以 f(x) 的傅立叶级数为：
其中，
(7). 若函数 f(x) 是周期为 2π 的周期函数，且为奇函数，则 f(x) 和 f(x)cosnx 为奇函数，f(x)sinnx 为偶函数，所以 f(x) 的傅立叶级数为：
其中，
(ex.49) f(x) 的周期为 2π，且
Sol：f(x) 可改写成
因为它是偶函数，所以
(1).
(2).
(3).
(4).
任意周期函数之傅立叶级数
(1). 周期为 2L 的周期函数 f(t) (注：L 为半周期)，其傅立叶级数为：
Pf：略
说明：周期为 2L 的傅立叶级数，只要将周期为 2π 的傅立叶级数作下列二项修改，
(a). 将公式的所有 π 改成 L；
(b). 将 sin 和 cos 内的 x 改成
(2). 周期为 2L 的偶函数 f(x)，其傅立叶级数为：
其中，
(3). 周期为 2L 的奇函数 f(x)，其傅立叶级数为：
其中，
(ex.50) 周期为 4 的 f(x)，且
Sol：週期 2L=4
(1).
(2).
(3).
(4).
(5). 所以
半周期函数 (或称半周期展开)
(1). 若給定一半週期函數，如週期是 2L 的函數，f(x) 只在 [0, L] 內有定義，現要將函數f(x)的定義擴展到 (-∞, ∞)，其擴展的方式有二種：
(a). 偶函数扩展：即先扩展到 [-L, L] 一周期的偶函数，再扩展到 (-∞, ∞)。
(b). 奇函数扩展：即先扩展到 [-L, L] 一周期的偶函数，再扩展到 (-∞, ∞)。
函数本来定义在 [0, L] 半周期内，经以上的扩展方式，周期均变为 2L，称为"半周期展开"。
(2). 要求半周期展开的傅立叶级数时，可以使用上节「任意周期函数之傅立叶级数」方法求得，及若是偶函数扩展或奇函数扩展，则代偶函数或奇函数的傅立叶级数公式。
(ex.51) 求下列函数的偶函数和奇函数半周期展开，且
Sol：半周期 L=2
(1). 展开成一周期偶函数
(a). 偶函数扩展：
(b).
(c).
(d). n=1, 2, 3, …代入，得
(e). 所以
(2). 展开成一周期奇函数
(a). 奇函数扩展：
(b).
(c). n=1, 2, 3, …代入，得
(d). 所以
复数傅立叶级数
(1). 也可以用复数方法来求傅立叶级数，其与用前面的方法求出来的答案相同。
(2). 函数 f(x) 是周期为 2π 的函数，其复数傅立叶级数为
，其中，
(3). 要求复数傅立叶级数时，
(a). 抄下
(b). 抄下
(c). 将题目的 f(x) 代入 (b) 式。
(d). 将 (b) 式积分出来。
(e). 求出
(f). 求出
(g).
注：
(i). 若题目要求「复数傅立叶级数」，只要做到 (d) 步骤，再将
(ii). 若题目要求「傅立叶级数」，则还要往下做以消去虚数 i，其結果与用前面方法求出答案相同。
(4). 函数 f(x) 是周期为 2L 的函数，其复数傅立叶级数为：
，其中，
说明：周期为 2L 的复数傅立叶级数只要将周期为 2π 的复数傅立叶级数作下列二项修改：
(a). 将公式的所有 π 改成 L；
(b). 将 e 的指数 x 改成
(ex.52) 若 f(x) 的周期为 2π，且
Sol：
(1).
(2).
(注：
(3). (a). n=-k 代入
(b). n=k 代入
(c). (a)+(b)
(4). n=0 代入
(5).
(答案与「周期为 2π 的傅立叶级数」中 (ex.48) 相同。)
傅立叶积分
(1). 若函数 f(x) 为非周期性函数或考虑整个 x 轴时，就要使用傅立叶积分。
(2). f(x) 的傅立叶积分为：
(3). 若 f(x) 是偶函数，则 B(w)=0；若 f(x) 是奇函数，则 A(w)=0。
(ex.53) 若
Sol：
所以 f(x) 的傅立叶积分
傅立叶余弦与正弦变换
(1). fc(w) 称为 f(x) 的“傅立叶余弦变换” (其中，c 表示 cos)，
(2). f(x) 称为 f(x) 的“反傅立叶余弦变换”，
(3). fs(w) 称为 f(x) 的“傅立叶正弦变换” (其中，s 表示 sin)，
(4). f(x) 称为 f(x) 的“反傅立叶正弦变换” (其中，c 表示 cos)，
(5). 它们在某些应用中仍然是首选，例如信号处理或统计。
(ex.54) 若
Sol：
(1). 傅立叶余弦转换，
(2). 傅立叶正弦转换，
离散傅立叶变换
(1). 在数字影像处理或通信系统的应用中，所处理的数据都是离散 (非连续) 数值。
(2). 令 f(x) 是周期为 2π 的周期函数 (0≦x≦2π)，对 f(x) 做 N 次相同“间隔点”(是离散数值)的量测，即间隔点为
注：
(3). 则 f(x) 的离散傅立叶变换
其中，
(a).
(b).
(c).
(d).
(ex.55) 令 N=4 次量测 (取样值)，量到的值为
Sol：
快速傅立叶变换
(1). 离散傅立叶变换的矩阵 NxN，若取样点有 1,000 点，其计算时间会很常，此时可以用快速傅立叶变换 (Fast Fourier Transform, FTF) 来解题。
(2). 快速傅立叶变换是将 N 分成 2 组，即 N=2M 来解。
(3). 将原向量
(注：有顶线的 f 表一向量，而无顶线的 f 表一纯量。)
(4). 分别对
(注：上面两个
(5). 由 (A)、(B) 我们可以得到某一组量测点 f 的离散傅立叶变换，即为：
(ex.56) 令 N=4 次量测 (取样值)，量到的值为
Sol：因 N=4，所以
由 (A) 式得
由 (B) 式得
由 (C) 式得
由 (D) 式得
Ref.:
李狗嗨：如何给文科生解释傅里叶变换？zhuanlan.zhihu.com
分类最后
以上就是细心鸵鸟为你收集整理的狄立克雷函数傅立叶变换0点_高等数学系列R之四：傅立叶级数及变换的全部内容，希望文章能够帮你解决狄立克雷函数傅立叶变换0点_高等数学系列R之四：傅立叶级数及变换所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
![[EE261学习笔记] 3.傅里叶变换推导](/uploads/reation/bcimg3.png)
发表评论 取消回复