Week14 作业（选做）-矩阵快速幂dp

思路：矩阵快速幂优化dp，
首先，定义a[i]为染i块砖时，红绿均偶数的方案数。
b[i]：红绿均奇数，c[i]：红绿一奇数一偶数。
那么我们可以得到三个状态转移方程：

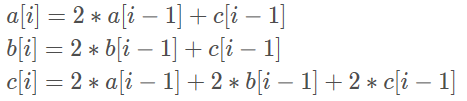
很明显，我们可以得到一个等式：

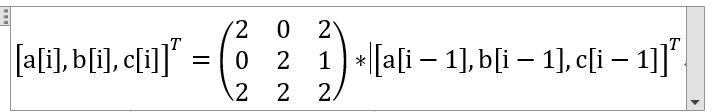
是不是很直观了呢，我们只需要知道a[1]=2,b[1]=0,c[1]=2就可以求出所有的情况。
完整代码：

#include<cmath>
#include<iostream>
#include<cstring>
#define ll long long
using namespace std;
const int N=3;
int n,m=10007;
struct matrix
{
 int a[N][N];
 matrix operator*(const matrix &b) const{
  matrix tmp;
  for(int i=0;i<N;i++){
   for(int j=0;j<N;j++){
    tmp.a[i][j]=0;
    for(int k=0;k<N;k++){
     tmp.a[i][j]+=(a[i][k]*b.a[k][j])%m;
    }
    tmp.a[i][j]%=m;
   }
  }
  return tmp;
 }
 matrix(){
  memset(a,0,sizeof(a));
 }
};
matrix quick_pow(matrix x,int e){
 matrix tmp;
 //memset(tmp.a,0,sizeof(tmp.a));
 tmp.a[0][0]=2;
 tmp.a[1][0]=0;
 tmp.a[2][0]=2;
 while(e){
  if(e&1){
   tmp=x*tmp;
  }
  x=x*x;
  e=e>>1;
 }
 return tmp;
}
int main(){
 int T;
 int tmp[N][N]={{2,0,1},{0,2,1},{2,2,2}};
 cin>>T;
 while(T--){
  cin>>n;
  matrix x;//2 0 1 0 2 1 2 2 2
  for(int i=0;i<N;i++)
   for(int j=0;j<N;j++)
   {
    x.a[i][j]=tmp[i][j]; 
   }
  matrix ans=quick_pow(x,n-1);
  cout<<ans.a[0][0]<<endl;
 }
 return 0;
}

定义dp[i][j]为第i天穿第j件衣服所获得的最大快乐值，我们得到状态转移方程：

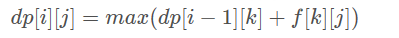
那么直接进行遍历肯定是会超时的，这里需要使用矩阵快速幂优化，只需要把矩阵乘重载成上面的形式就行了。
具体见代码：

#include<cmath>
#include<iostream>
#include<cstring>
#define ll long long
using namespace std;
const int N=105;
int n,m;
struct matrix
{
 ll a[N][N];
 matrix operator*(const matrix &b) const{
  matrix tmp;
  for(int i=0;i<m;i++){
   for(int j=0;j<m;j++){
    tmp.a[i][j]=0;
    for(int k=0;k<m;k++){
     tmp.a[i][j]=max(tmp.a[i][j],a[i][k]+b.a[k][j]);
    }
   }
  }
  return tmp;
 }
 matrix(){
  memset(a,0,sizeof(a));
 }
};
matrix quick_pow(matrix x,int e){
 matrix tmp;
 //memset(tmp.a,0,sizeof(tmp.a));
 while(e){
  if(e&1){
   tmp=tmp*x;
  }
  x=x*x;
  e=e>>1;
 }
 return tmp;
}
int main(){
 while(cin>>n>>m){
  matrix h,ansm;
  for(int i=0;i<m;i++){
   for(int j=0;j<m;j++){
    cin>>h.a[i][j];
   }
  }
  ansm=quick_pow(h,n-1);
  ll ans=0;
  for(int i=0;i<m;i++)
   for(int j=0;j<m;j++){
    ans=max(ans,ansm.a[i][j]);
   }
  cout<<ans<<endl; 
 }
 return 0;
}

最后

以上就是兴奋小鸽子为你收集整理的Week14 作业（选做）-矩阵快速幂dp的全部内容，希望文章能够帮你解决Week14 作业（选做）-矩阵快速幂dp所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。