HDU2604 递推关系+矩阵快速幂

71 阅读 0 评论 47 点赞

我是靠谱客的博主聪明雨，最近开发中收集的这篇文章主要介绍HDU2604 递推关系+矩阵快速幂，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

HDU2604Queuing
题目大意求n阶序列，每一位可以填f或者m，求不存在fff或者fmf的字串的个数，根据题目建立递推关系式:
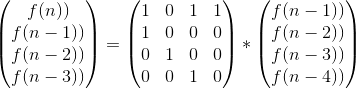
这里写图片描述
之后用矩阵快速幂套路掉
AC代码:

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N=4;
int l,mod;
struct mat{
    int m[N][N];
    mat() {}
    mat unit(){
        for(int i=0;i<N;i++)
            for(int j=0;j<=N;j++)
                m[i][j]=i==j?1:0;
    }
};
mat t;
mat operator * (mat a,mat b){
    mat res;
    for(int i=0;i<N;i++)
        for(int j=0;j<=N;j++){
            res.m[i][j]=0;
            for(int k=0;k<N;k++)
                res.m[i][j]+=(a.m[i][k]*b.m[k][j])%mod;
        }
    return res;
}
mat operator ^ (mat res,int n){
    res.unit();
    while(n>=1){
        if(n&1)
            res=res*t;
        n=n>>1;
        t=t*t;
    }
    return res;
}
void init(){
    t.m[0][0]=1;t.m[0][1]=0;t.m[0][2]=1;t.m[0][3]=1;
    t.m[1][0]=1;t.m[1][1]=0;t.m[1][2]=0;t.m[1][3]=0;
    t.m[2][0]=0;t.m[2][1]=1;t.m[2][2]=0;t.m[2][3]=0;
    t.m[3][0]=0;t.m[3][1]=0;t.m[3][2]=1;t.m[3][3]=0;
}
int main(){
     mat A;
    //freopen("input.txt","r",stdin);
    while(~scanf("%d%d",&l,&mod)){
        init();
        memset(A.m,0,sizeof(A.m));
        int ans=0;
        if(l==0){
            printf("0n");
            continue;
        }
        if(l==1){
            printf("%dn",2%mod);
            continue;
        }
        else if(l==2){
            printf("%dn",4%mod);
            continue;
        }
        else if(l==3){
            printf("%dn",6%mod);
            continue;
        }
        else{
            A=t^(l-4);
            //for(int i=0;i<N;i++){
                //for(int j=0;j<N;j++)
                    //printf("%d ",A.m[i][j]);
            //cout<<endl;
            //}
            ans=(9*A.m[0][0]+6*A.m[0][1]+4*A.m[0][2]+2*A.m[0][3])%mod;
            printf("%dn",ans);
        }   
    } 
}