概述
Mahmoud and Ehab play a game called the even-odd game. Ehab chooses his favorite integer n and then they take turns, starting from Mahmoud. In each player's turn, he has to choose an integer a and subtract it from n such that:
- 1 ≤ a ≤ n.
- If it's Mahmoud's turn, a has to be even, but if it's Ehab's turn, a has to be odd.
If the current player can't choose any number satisfying the conditions, he loses. Can you determine the winner if they both play optimally?
The only line contains an integer n (1 ≤ n ≤ 109), the number at the beginning of the game.
Output "Mahmoud" (without quotes) if Mahmoud wins and "Ehab" (without quotes) otherwise.
1
Ehab
2
Mahmoud
In the first sample, Mahmoud can't choose any integer a initially because there is no positive even integer less than or equal to 1 so Ehab wins.
In the second sample, Mahmoud has to choose a = 2 and subtract it from n. It's Ehab's turn and n = 0. There is no positive odd integer less than or equal to 0 so Mahmoud wins.
水题，判断奇偶即可。
#include <cstdio>
#include <iostream>
#include <string.h>
#include <string>
#include <map>
#include <queue>
#include <deque>
#include <vector>
#include <set>
#include <algorithm>
#include <math.h>
#include <cmath>
#include <stack>
#include <iomanip>
#define mem0(a) memset(a,0,sizeof(a))
#define meminf(a) memset(a,0x3f,sizeof(a))
using namespace std;
typedef long long ll;
typedef long double ld;
typedef double db;
const int maxn=100005,inf=0x3f3f3f3f;
const ll llinf=0x3f3f3f3f3f3f3f3f;
const ld pi=acos(-1.0L);
int main() {
ll n,i;
cin >> n;
if (n%2) cout << "Ehab"; else cout << "Mahmoud";
return 0;
}Mahmoud wants to send a message to his friend Ehab. Their language consists of n words numbered from 1 to n. Some words have the same meaning so there are k groups of words such that all the words in some group have the same meaning.
Mahmoud knows that the i-th word can be sent with cost ai. For each word in his message, Mahmoud can either replace it with another word of the same meaning or leave it as it is. Can you help Mahmoud determine the minimum cost of sending the message?
The cost of sending the message is the sum of the costs of sending every word in it.
The first line of input contains integers n, k and m (1 ≤ k ≤ n ≤ 105, 1 ≤ m ≤ 105) — the number of words in their language, the number of groups of words, and the number of words in Mahmoud's message respectively.
The second line contains n strings consisting of lowercase English letters of length not exceeding 20 which represent the words. It's guaranteed that the words are distinct.
The third line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) where ai is the cost of sending the i-th word.
The next k lines describe the groups of words of same meaning. The next k lines each start with an integer x (1 ≤ x ≤ n) which means that there are x words in this group, followed by x integers which represent the indices of words in this group. It's guaranteed that each word appears in exactly one group.
The next line contains m space-separated words which represent Mahmoud's message. Each of these words appears in the list of language's words.
The only line should contain the minimum cost to send the message after replacing some words (maybe none) with some words of the same meaning.
5 4 4 i loser am the second 100 1 1 5 10 1 1 1 3 2 2 5 1 4 i am the second
107
5 4 4 i loser am the second 100 20 1 5 10 1 1 1 3 2 2 5 1 4 i am the second
116
In the first sample, Mahmoud should replace the word "second" with the word "loser" because it has less cost so the cost will be 100+1+5+1=107.
In the second sample, Mahmoud shouldn't do any replacement so the cost will be 100+1+5+10=116.
水题，使用map即可
#include <cstdio>
#include <iostream>
#include <string.h>
#include <string>
#include <map>
#include <queue>
#include <deque>
#include <vector>
#include <set>
#include <algorithm>
#include <math.h>
#include <cmath>
#include <stack>
#include <iomanip>
#define mem0(a) memset(a,0,sizeof(a))
#define meminf(a) memset(a,0x3f,sizeof(a))
using namespace std;
typedef long long ll;
typedef long double ld;
typedef double db;
const int maxn=100005,inf=0x3f3f3f3f;
const ll llinf=0x3f3f3f3f3f3f3f3f;
const ld pi=acos(-1.0L);
ll a[maxn],b[maxn],c[maxn];
string s[maxn];
map<string,int> mp;
int main() {
ios::sync_with_stdio(false);
meminf(a);
int n,k,m,i,j,x,y;
cin >> n >> k >> m;
for (i=1;i<=n;i++) {
cin >> s[i];
}
for (i=1;i<=n;i++) {
cin >> b[i];
}
for (i=1;i<=k;i++) {
cin >> x;
for (j=1;j<=x;j++) {
cin >> y;
a[i]=min(a[i],b[y]);
mp[s[y]]=i;
}
}
ll sum=0;
string t;
for (i=1;i<=m;i++) {
cin >> t;
sum+=a[mp[t]];
}
cout << sum << endl;
return 0;
}Mahmoud was trying to solve the vertex cover problem on trees. The problem statement is:
Given an undirected tree consisting of n nodes, find the minimum number of vertices that cover all the edges. Formally, we need to find a set of vertices such that for each edge (u, v) that belongs to the tree, either u is in the set, or v is in the set, or both are in the set. Mahmoud has found the following algorithm:
- Root the tree at node 1.
- Count the number of nodes at an even depth. Let it be evenCnt.
- Count the number of nodes at an odd depth. Let it be oddCnt.
- The answer is the minimum between evenCnt and oddCnt.
The depth of a node in a tree is the number of edges in the shortest path between this node and the root. The depth of the root is 0.
Ehab told Mahmoud that this algorithm is wrong, but he didn't believe because he had tested his algorithm against many trees and it worked, so Ehab asked you to find 2 trees consisting of n nodes. The algorithm should find an incorrect answer for the first tree and a correct answer for the second one.
The only line contains an integer n (2 ≤ n ≤ 105), the number of nodes in the desired trees.
The output should consist of 2 independent sections, each containing a tree. The algorithm should find an incorrect answer for the tree in the first section and a correct answer for the tree in the second. If a tree doesn't exist for some section, output "-1" (without quotes) for that section only.
If the answer for a section exists, it should contain n - 1 lines, each containing 2 space-separated integers u and v (1 ≤ u, v ≤ n), which means that there's an undirected edge between node u and node v. If the given graph isn't a tree or it doesn't follow the format, you'll receive wrong answer verdict.
If there are multiple answers, you can print any of them.
2
-1 1 2
8
1 2 1 3 2 4 2 5 3 6 4 7 4 8 1 2 1 3 2 4 2 5 2 6 3 7 6 8
In the first sample, there is only 1 tree with 2 nodes (node 1 connected to node 2). The algorithm will produce a correct answer in it so we printed - 1 in the first section, but notice that we printed this tree in the second section.
In the second sample:
In the first tree, the algorithm will find an answer with 4 nodes, while there exists an answer with 3 nodes like this: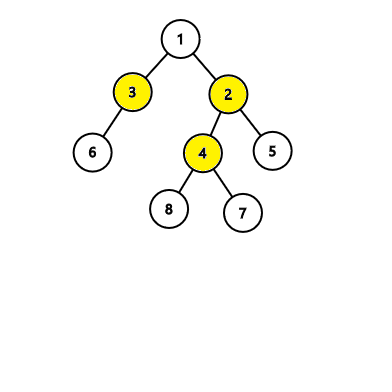
In the second tree, the algorithm will find an answer with 3 nodes which is correct: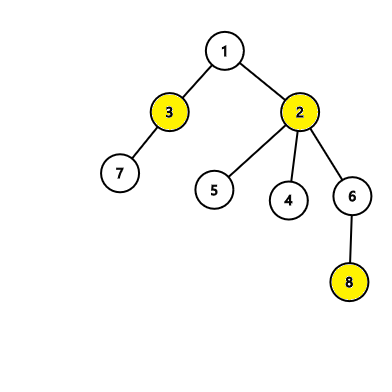
构造满足条件的树很简单，所有点连接根节点即可。
至于不满足条件的树，可以将其这样构造：
若一共有n个节点，第一层是根，第二层摆放n/2个儿子，第三层摆剩下所有点，且连在上一层同一个父亲之下。
#include <cstdio>
#include <iostream>
#include <string.h>
#include <string>
#include <map>
#include <queue>
#include <deque>
#include <vector>
#include <set>
#include <algorithm>
#include <math.h>
#include <cmath>
#include <stack>
#include <iomanip>
#define mem0(a) memset(a,0,sizeof(a))
#define meminf(a) memset(a,0x3f,sizeof(a))
using namespace std;
typedef long long ll;
typedef long double ld;
typedef double db;
const int maxn=100005,inf=0x3f3f3f3f;
const ll llinf=0x3f3f3f3f3f3f3f3f;
const ld pi=acos(-1.0L);
int main() {
int n,i,j;
cin >> n;
if (n<=5) {
printf("-1n");
} else {
for (i=1;i<=n/2;i++) {
printf("%d %dn",1,i+1);
}
for (i=1;i<n-n/2;i++) {
printf("%d %dn",2,n/2+i+1);
}
}
for (i=1;i<n;i++) {
printf("%d %dn",1,i+1);
}
return 0;
}Mahmoud has an array a consisting of n integers. He asked Ehab to find another array b of the same length such that:
- b is lexicographically greater than or equal to a.
- bi ≥ 2.
- b is pairwise coprime: for every 1 ≤ i < j ≤ n, bi and bj are coprime, i. e. GCD(bi, bj) = 1, where GCD(w, z) is the greatest common divisor of w and z.
Ehab wants to choose a special array so he wants the lexicographically minimal array between all the variants. Can you find it?
An array x is lexicographically greater than an array y if there exists an index i such than xi > yi and xj = yj for all 1 ≤ j < i. An array x is equal to an array y if xi = yi for all 1 ≤ i ≤ n.
The first line contains an integer n (1 ≤ n ≤ 105), the number of elements in a and b.
The second line contains n integers a1, a2, ..., an (2 ≤ ai ≤ 105), the elements of a.
Output n space-separated integers, the i-th of them representing bi.
5 2 3 5 4 13
2 3 5 7 11
3 10 3 7
10 3 7
Note that in the second sample, the array is already pairwise coprime so we printed it.
显然需要判断往序列末尾添加数时，它是不是与之前的数字互质。我们只需打印素数表，将每个Ai分解质因数，观察Ai的每个质因数是不是只出现过一次。
遇到第一个不满足条件的位置i时，贪心修改。找一个大于Ai的满足条件的最小的数，暴力枚举。
之后的所有位置，可以使用之前过程中未分解过的素数。注意修改Ai之后也要把它分解质因数，再放入hash表。(我直接利用vector数组的大小判断) 要求字典序最小，按序输出即可。
最多可能输出100000个素数，亲自操作发现，n=3000000时，有约200000个素数，满足题目条件。
#include <cstdio>
#include <iostream>
#include <string.h>
#include <string>
#include <map>
#include <queue>
#include <deque>
#include <vector>
#include <set>
#include <algorithm>
#include <math.h>
#include <cmath>
#include <stack>
#include <iomanip>
#define mem0(a) memset(a,0,sizeof(a))
#define meminf(a) memset(a,0x3f,sizeof(a))
#define N 3000000
#define num0 9592
using namespace std;
typedef long long ll;
typedef long double ld;
typedef double db;
const int maxn=100005,inf=0x3f3f3f3f;
const ll llinf=0x3f3f3f3f3f3f3f3f;
const ld pi=acos(-1.0L);
ll a[N],b[maxn];
bool prime[N+5];
vector<int> v[N+5];
int num=0;
void init() {
num=0;
memset(prime,0,sizeof(prime));
int i,j;
for (i=2;i<=N;i++) {
if (!prime[i])
a[++num]=i;
for (j=1;j<=num&&i*a[j]<=N;j++) {
prime[i*a[j]]=1;
if (i%a[j]==0)
break;
}
}
}
int main() {
int n,i,j,k,flag=-1,l;
init();
scanf("%d",&n);
for (i=1;i<=n;i++) {
scanf("%d",&b[i]);
int x=b[i];
for (j=1;j<=num0;j++) {
if (x%a[j]==0) {
while (x%a[j]==0) x/=a[j];
if (v[a[j]].size()>0) {
flag=v[a[j]][0];break;
}
if (x==1) break;
}
}
if (flag!=-1)
break;
for (j=1;j<=num0;j++)
if (b[i]%a[j]==0) {
v[a[j]].push_back(i);
}
}
if (flag==-1) {
for (i=1;i<=n;i++) {
printf("%d ",b[i]);
}
return 0;
}
for (j=b[i]+1;;j++) {
int x=j,fff=-1;
for (l=1;l<=num0;l++) {
if (x%a[l]==0) {
while (x%a[l]==0) x/=a[l];
if (v[a[l]].size()>0) {
fff=1;break;
}
if (x==1) break;
}
}
if (fff==-1) {
b[i]=j;
int y=j;
for (l=1;y!=1;l++)
if (y%a[l]==0) {
v[a[l]].push_back(i);
while (y%a[l]==0) y/=a[l];
}
break;
}
}
for (k=1;k<=i;k++) {
printf("%d ",b[k]);
}
l=0;
for (k=i+1;k<=n;k++) {
l++;
while (v[a[l]].size()>0)
l++;
printf("%d ",a[l]);
}
return 0;
}Ehab is interested in the bitwise-xor operation and the special graphs. Mahmoud gave him a problem that combines both. He has a complete graph consisting of n vertices numbered from 0 to n - 1. For all 0 ≤ u < v < n, vertex u and vertex v are connected with an undirected edge that has weight 
(where 
is the bitwise-xor operation). Can you find the weight of the minimum spanning tree of that graph?
You can read about complete graphs in https://en.wikipedia.org/wiki/Complete_graph
You can read about the minimum spanning tree in https://en.wikipedia.org/wiki/Minimum_spanning_tree
The weight of the minimum spanning tree is the sum of the weights on the edges included in it.
The only line contains an integer n (2 ≤ n ≤ 1012), the number of vertices in the graph.
The only line contains an integer x, the weight of the graph's minimum spanning tree.
4
4
In the first sample:
The weight of the minimum spanning tree is 1+2+1=4.
对于一个二进制正数，与它异或最小的正数是本身，结果是0；其次是把最后一位取反之后，结果是1。
长度为1的边肯定要连，这样，01,23,45,67...相邻的数被连在一起。
接下来，怎么把这些相邻的块，每个块含有相邻的两个数字，再次最优的连在一起呢？
相邻两个块的异或值最小为4，这一结果可以由其中一个块中任意一个数取反倒数第二位得到。
这样，0123,4567,89 10 11... 相邻四个数连成了块。
不断操作就得到了最小生成树，每次合并边的长度最小是上一次的两倍。
若节点总数不是2的次方，只需要取不超过n的最小的2^i,把他们两两合并，待点数减少再和多余的点连。
这样，可以推得长度一定的边随着n增加被选的频率：
l=1 n=2,4,6,8...
l=2 n=3,7,11,15...
l=4 n=5,13,21..
l=8 n=9,25.....
发现若l=2^i,则n每次也增加2^(i+1)，且第一个n就是l+1.
如此可推得公式：
$$ans=sum_{i} [(n-1+2^{i-1})/2^{i}]*(2^{i-1})$$
其中中括号当中是长度为2^(-1)的边出现的次数。
#include <cstdio>
#include <iostream>
#include <string.h>
#include <string>
#include <map>
#include <queue>
#include <deque>
#include <vector>
#include <set>
#include <algorithm>
#include <math.h>
#include <cmath>
#include <stack>
#include <iomanip>
#define mem0(a) memset(a,0,sizeof(a))
#define meminf(a) memset(a,0x3f,sizeof(a))
using namespace std;
typedef long long ll;
typedef long double ld;
typedef double db;
const int inf=0x3f3f3f3f;
const ll llinf=0x3f3f3f3f3f3f3f3f;
const ld pi=acos(-1.0L);
int main() {
ll n,i,j,ans=0;
scanf("%I64d",&n);
for (i=1;i<=60;i++) {
ans+=((n+(1ll<<(i-1ll))-1ll)/(1ll<<i))*(1ll<<(i-1ll));
// cout << i << ' ' << ans << endl;
}
printf("%I64dn",ans);
return 0;
}最后
以上就是执着万宝路为你收集整理的Codeforces Round #473 (Div. 2) ABCDE的全部内容，希望文章能够帮你解决Codeforces Round #473 (Div. 2) ABCDE所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复