我是靠谱客的博主 谨慎胡萝卜，最近开发中收集的这篇文章主要介绍【leetcode系列】【算法】【面试题】二维数组中的查找(利用栈的分治 + 二分查找)题目：解题思路：代码实现：，觉得挺不错的，现在分享给大家，希望可以做个参考。
概述
题目：
题目链接： https://leetcode-cn.com/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/
解题思路：
方法一：线性查找
从矩阵的右上角开始查找，流程如下：
- 如果目标值大于当前值，则目标值大于当前行前面的所有值，所以向下查找
- 如果目标值小于当前值，则目标值小于当前列下面的所有值，所以向左查找
这样子能够保证不会错过目标值
方法二：分治 + 二分查找
从矩阵中心获取一点，按照这一点的行列进行划分4个区域，其中左上角的区域中，所有数字均小于中心点，右下角区域所有值均大于中心点；而左下和右上两个区域的值无法区分大小
根据这一点，至少可以排除掉左上或者右下的区域，然后进行剩余3个区域的分治，图示流程如下：
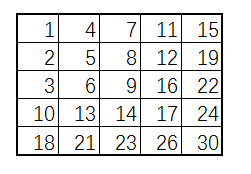
假设初始矩阵如下，目标值target = 5：
中心值 = 9 > 5，此时将右下角区域全部舍去，对剩余三个区域进行分治：
当一个矩阵小于2 × 2时，对当前矩阵进行遍历判断，不再进行划分
此时左上角区域中矩阵为2 × 2的，对此矩阵进行遍历判断，找到目标值5
时间复杂度计算（字不好看，请见谅=，=）：
代码实现：
方法一：
python:
class Solution:
def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
if 0 == len(matrix):
return False
row, column = 0, len(matrix[0]) - 1
while row < len(matrix) and column >= 0:
if target == matrix[row][column]:
return True
elif target > matrix[row][column]:
row += 1
else:
column -= 1
return Falsec++:
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
if (0 == matrix.size()) {
return false;
}
int row = 0;
int column = matrix[0].size() - 1;
while (row < matrix.size() and column >= 0) {
if (target == matrix[row][column]) {
return true;
} else if (target > matrix[row][column]) {
++row;
} else {
--column;
}
}
return false;
}
};
方法二：
python :
class Solution:
def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
if 0 == len(matrix):
return False
stack = [[0, len(matrix), 0, len(matrix[0])]]
while stack:
start_row, end_row, start_column, end_column = stack[-1]
stack.pop()
if start_row >= end_row or start_column >= end_column:
continue
curr_matrix = [matrix[i][start_column:end_column] for i in range(start_row, end_row)]
if 2 >= end_row - start_row and 2 >= end_column - start_column:
for i in range(start_row, end_row):
for j in range(start_column, end_column):
if target == matrix[i][j]:
return True
continue
mid_row = (start_row + end_row) // 2
mid_column = (start_column + end_column) // 2
mid_num = matrix[mid_row][mid_column]
if mid_num == target:
return True
# 右上角矩阵
stack.append([start_row, mid_row, mid_column, end_column])
# 左下角矩阵
stack.append([mid_row, end_row, start_column, mid_column])
if mid_num > target:
# 左上角矩阵
stack.append([start_row, mid_row, start_column, mid_column])
else:
# 右下角矩阵
stack.append([mid_row, end_row, mid_column, end_column])
return Falsec++ :
#define START_ROW_IDX 0
#define END_ROW_IDX 1
#define START_COLUMN_IDX 2
#define END_COLUMN_IDX 3
#define RET_CONTINUE 0
#define RET_TRUE 1
#define RET_FALSE 2
class Solution {
public:
void add_matrix_row_column(stack<vector<int>>& stack, int start_row, int end_row, int start_column, int end_column) {
vector<int> curr_matrix;
curr_matrix.push_back(start_row);
curr_matrix.push_back(end_row);
curr_matrix.push_back(start_column);
curr_matrix.push_back(end_column);
stack.push(curr_matrix);
}
int judge_matrix(const vector<vector<int>>& matrix, const vector<int>& curr_matrix, int target) {
if (2 < curr_matrix[END_ROW_IDX] - curr_matrix[START_ROW_IDX]) {
return RET_FALSE;
} else if (2 < curr_matrix[END_COLUMN_IDX] - curr_matrix[START_COLUMN_IDX]) {
return RET_FALSE;
}
// 如果当前矩阵小于2 * 2,则遍历判断
for (int row = curr_matrix[START_ROW_IDX]; row < curr_matrix[END_ROW_IDX]; ++row) {
for (int column = curr_matrix[START_COLUMN_IDX]; column < curr_matrix[END_COLUMN_IDX]; ++column) {
if (matrix[row][column] == target) {
return RET_TRUE;
}
}
}
return RET_CONTINUE;
}
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
if (0 >= matrix.size()) {
return false;
}
stack<vector<int>> rec;
add_matrix_row_column(rec, 0, matrix.size(), 0, matrix[0].size());
while (!rec.empty()) {
vector<int> curr_matrix = rec.top();
rec.pop();
if ((curr_matrix[START_ROW_IDX] >= curr_matrix[END_ROW_IDX])
|| (curr_matrix[START_COLUMN_IDX] >= curr_matrix[END_COLUMN_IDX])) {
continue;
}
int ret = judge_matrix(matrix, curr_matrix, target);
if (ret == RET_CONTINUE) {
continue;
} else if (ret == RET_TRUE) {
return true;
}
int mid_row = (curr_matrix[START_ROW_IDX] + curr_matrix[END_ROW_IDX]) / 2;
int mid_column = (curr_matrix[START_COLUMN_IDX] + curr_matrix[END_COLUMN_IDX]) / 2;
int mid_num = matrix[mid_row][mid_column];
if (mid_num == target) {
return true;
}
// 右上角
add_matrix_row_column(rec, curr_matrix[START_ROW_IDX], mid_row, mid_column, curr_matrix[END_COLUMN_IDX]);
// 左下角
add_matrix_row_column(rec, mid_row, curr_matrix[END_ROW_IDX], curr_matrix[START_COLUMN_IDX], mid_column);
if (mid_num > target) {
// 左上角
add_matrix_row_column(rec, curr_matrix[START_ROW_IDX], mid_row, curr_matrix[START_COLUMN_IDX], mid_column);
} else {
// 右下角
add_matrix_row_column(rec, mid_row, curr_matrix[END_ROW_IDX], mid_column, curr_matrix[END_COLUMN_IDX]);
}
}
return false;
}
};
最后
以上就是谨慎胡萝卜为你收集整理的【leetcode系列】【算法】【面试题】二维数组中的查找(利用栈的分治 + 二分查找)题目：解题思路：代码实现：的全部内容，希望文章能够帮你解决【leetcode系列】【算法】【面试题】二维数组中的查找(利用栈的分治 + 二分查找)题目：解题思路：代码实现：所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复