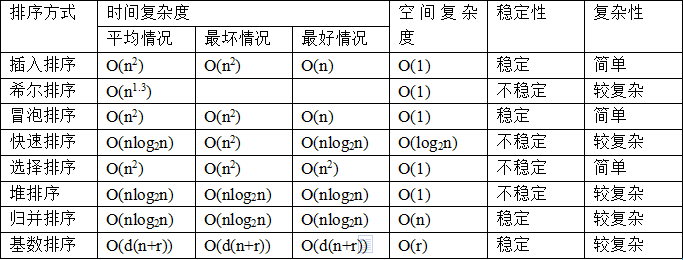
不稳定:快速、希尔、选择、堆
一、冒泡排序
算法描述如下:
1.比较相邻的两个元素,如果前一个比后一个大,则交换位置。
2.第一轮的时候最后一个元素应该是最大的一个。
3.按照步骤一的方法进行相邻两个元素的比较,这个时候由于最后一个元素已经是最大的了,所以最后一个元素不用比较。
算法实现:
/**
* @Author spring
* @DateTime 2020-10-29
* @param {arr} 待数组
* @return {arr} 排好序的数组
* @description 这是一个冒泡排序算法
*/
function bubbleSort(arr) {
var len = arr.length;
for (var i = 0; i < len - 1; i++) { //外层:比较的趟数,每次将最大值放到数组最后
for (var j = 0; j < len - i - 1; j++) { //内层:将相邻的两个元素,两两比较
if (arr[j] > arr[j + 1]) { //元素交换
var temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
return arr;
}
var arr = [1, 12, 7, 4, 6];
var result = bubbleSort(arr);
console.log(result); //[ 1, 4, 6, 7, 12 ]冒泡排序是稳定的排序算法,它的最差时间复杂度 o(n^2);平均时间复杂度o(n^2),最优时间复杂度o(n)
二、选择排序
算法描述如下:
初始时在未排序序列中找最小元素,放到序列的起始位置作为已排序序列;
然后再从剩余未排序元素中继续寻找最小元素,放到已排序序列的末尾。
以此类推。直到所有元素均排序完毕。

算法实现:
/**
* @Author spring
* @DateTime 2020-10-29
* @param {arr} 未排序数组
* @return {arr} 已排序数组
* @description 这是一个选择排序算法
*/
function selectionSort(arr) {
var len = arr.length;
for (var i = 0; i < len-1; i++) {
var minIndex = i;
for (var j = i + 1; j < len; j++) {
//从待排序序列中找到最小值
if (arr[j] < arr[minIndex]) {
minIndex = j; //保存最小值的索引
}
}
var temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
return arr;
}
//测试
var arr = [1, 12, 7, 4, 6];
selectionSort(arr);
console.log(arr); //[ 1, 4, 6, 7, 12 ]选择排序不稳定,最差时间复杂度 o(n^2);最优时间复杂度 o(n^2);平均时间复杂度 o(n^2)
三、插入排序
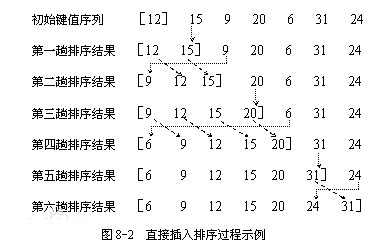
插入排序的工作方式非常像人们排序一手扑克牌一样。开始时,我们的左手为空并且桌子上的牌面朝下。然后,我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置,我们从右到左将它与已在手中的每张牌进行比较.
首先我们将数组中的数据分为两个区间,已排序区间和未排序区间。初始已排序区间只有一个元素,就是数组的第一个元素,然后在未排序区间中依次取出元素并插入到已排序区间的合适位置,并保证已排序区间一直是有序。重复这个步骤直到未排序区间元素为空,算法结束。
算法描述如下:
(1) 从第一个元素开始,该元素可以认为已经被排序
(2) 取出下一个元素,在已经排序的元素序列中从后向前扫描
(3) 如果该元素(已排序)大于新元素,将该元素移到下一位置
(4) 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
(5)将新元素插入到下一位置中
(6) 重复步骤2
算法实现:
/**
* @Author spring
* @DateTime 2020-10-29
* @param {arr} 待排序序列
* @return {arr} 排好序序列
* @description 这是一个插入排序算法
*/
function insertSort(arr) {
var len = arr.length;
var preIndex, current;
//假设第1个元素是一个有序的数列,第2个之后是无序的序列
//从第2个元素开始,将无序序列里的元素插入到有序序列中
for (var i = 1; i < len; i++) {
preIndex = i - 1; //有序数列的最后一个位置
current = arr[i]; //无序数列中的第i个作为被插入元素
//比大小,找到被插入元素所在的位置
while (preIndex >= 0 && arr[preIndex] > current) {
arr[preIndex + 1] = arr[preIndex]; 若不是合适位置,有序组元素向后移动
preIndex--;
}
arr[preIndex + 1] = current; //找到合适位置,将元素插入
}
return arr;
}
var arr = [1, 12, 7, 4, 6];
var result = insertSort(arr); //从小到大排序
console.log(result); //[ 1, 4, 6, 7, 12 ]
插入排序稳定,最差时间复杂度o(n^2)待排序列是降序序列;最优时间复杂度o(n)即待排序列是升序,平均时间复杂度o(n^2)。
四、快速排序
算法描述如下:
1. 从数列中取出一个数作为基数。
2. 重新排序数列,所有元素比基准值小的放到基准值前,所有元素比基准值大的放到其后。
3. 在对基准值左右区间,重复第二步,直到个区间只有一个数
假设我们对数组 T = [6,1,2,7,9,3,4,5,10,8] 进行快速排序。
(1)、确定基准数
我们把数组的第一个元素作为基准数。
基准数的作用就是我们一次计算结束后,把小于基准数额元素都放到基准数的左边,大于等于基准数的元素都放到基准数的右边。例如,我们一次计算之后的T是这样的:
T = [3,1,2,5,4 ,6 ,9,7,10,8]
(2)、确定哨兵
用两个变量i和j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵i”和“哨兵j”。刚开始的时候让哨兵i指向序列的最左边,让哨兵j指向序列的最右边。
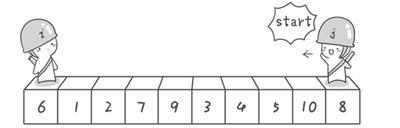
首先哨兵j开始出动。哨兵j一步一步地向左挪动(即j--),直到找到一个小于6的数停下来。接下来哨兵i再一步一步向右挪动(即i++),直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前,哨兵i停在了数字7面前。
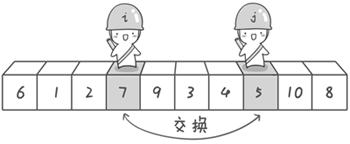
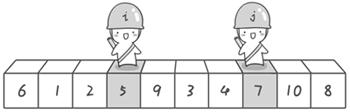
接下来开始哨兵j继续向左挪动。他发现了4(比基准数6要小,满足要求)之后停了下来。哨兵i也继续向右挪动的,他发现了9(比基准数6要大,满足要求)之后停了下来。此时再次进行交换。
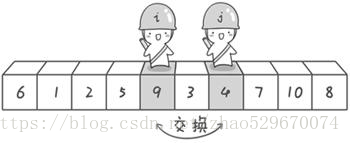
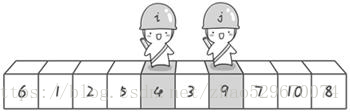
第二次交换结束,“探测”继续。哨兵j继续向左挪动,他发现了3(比基准数6要小,满足要求)之后又停了下来。哨兵i继续向右移动,糟啦!此时哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。交换之后的序列如下:
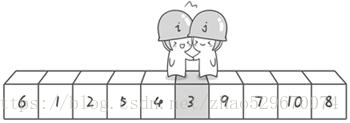
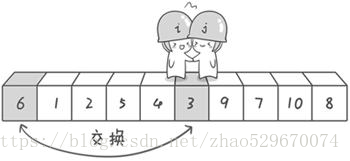
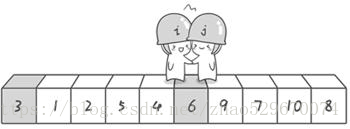
到此第一轮“探测”真正结束。此时以基准数6为分界点,6左边的数都小于等于6,6右边的数都大于等于6。然后对6两边的数组做递归处理即可。
算法实现:
/**
* @Author spring
* @DateTime 2020-10-31
* @param arr 待排序数组
* @param left 数组第一个元素下标(0)
* @param right 数组最后一个元素下标
* @return arr 排好序的数组
*/
function quickSort(arr,left,right){
if (left < right) {
var i = left, j = right;
var x = arr[left]; //基准数,这里取数组第一个数
while (i < j) {
// 从右边向左边找小于x的数,找到或者两个哨兵相碰,跳出循环
while(i < j && arr[j] > x){
j--;
}
//从左边向右边找大于x的数,找到或者两个哨兵相碰,跳出循环
while(i < j && arr[i] <= x){
i++;
}
if (i < j) { //交换两个元素的位置
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
arr[left] = arr[i]; //最左边的那个元素=目前i==j时的这个元素。
arr[i] = x; //i==j时的这个元素等于最左边的那个元素。
quickSort(arr, left, i-1);
quickSort(arr, i+1, right);
}
return arr;
}
var arr=[1, 12, 7, 4, 6];
console.log("原数组",arr);
quickSort(arr, 0, arr.length-1);
console.log(arr); //[ 1, 4, 6, 7, 12 ]快速排序是不稳定的排序算法,它的平均时间复杂度o(nlog2n),最优时间复杂度o(nlog2n),最差时间复杂度 o(n^2)。
五、归并排序
算法描述如下:
将两个已经排序的序列合并成一个序列,采用分支法,递归地把当前序列平均分割成两半,然后再保证左右顺序情况下合并在一起。
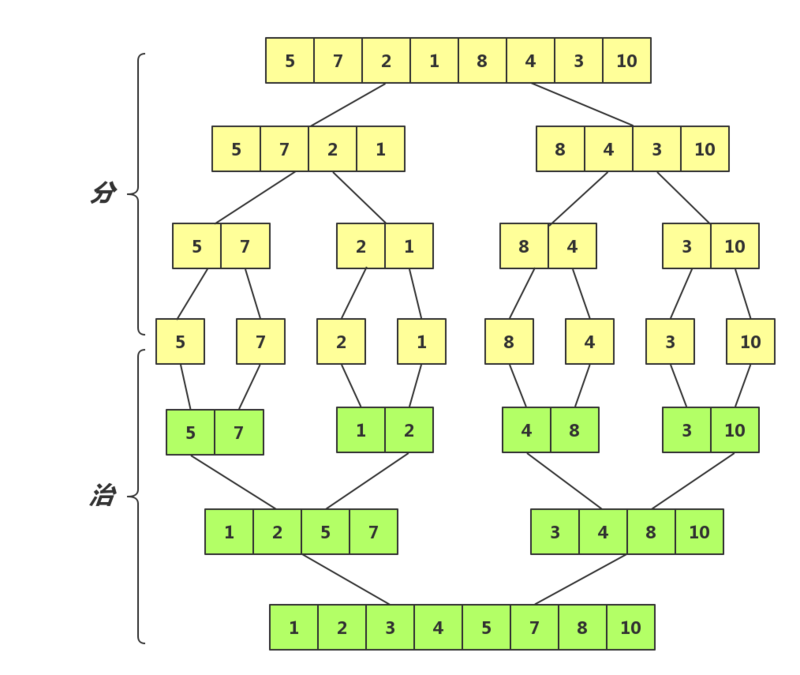
归并排序是稳定的排序算法,它的平均时间复杂度o(nlog2n),最优时间复杂度o(nlog2n),最差时间复杂度 o(nlog2n)。
最后
以上就是忧郁八宝粥最近收集整理的关于js排序算法:冒泡、选择、插入、快排★★★ 归并★一、冒泡排序二、选择排序三、插入排序四、快速排序五、归并排序的全部内容,更多相关js排序算法:冒泡、选择、插入、快排★★★内容请搜索靠谱客的其他文章。








发表评论 取消回复