1.冒泡排序

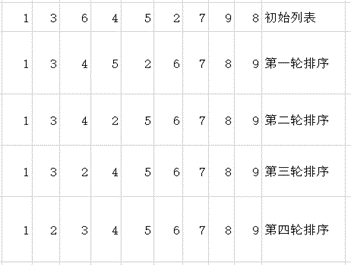
【原理】 元素两两比较，只要前一个元素大于后一个元素就对换位置。从首元素到最后元素逐个两两比较进行一轮一轮的排序。

def bubble_sort(alist):
    for time in range(len(alist)-1):#(1)
        for j in range(len(alist)-1):
            if alist[j+1]< alist[j]:
                alist[j+1],alist[j]=alist[j],alist[j+1]
                exchange = True
        print(alist, '第%d轮输出' % (time+1))

alist = [1,3,6,4,5,2,7,9,8]
bubble_sort(alist) 

(1) time为进行的排序轮数，因为只剩下两个元素的时候，把其中一个放好位置后，另一个自动归位，所以进行的轮数为元素个数减1
输出结果为：

[1, 3, 4, 5, 2, 6, 7, 8, 9] 第1轮输出
[1, 3, 4, 2, 5, 6, 7, 8, 9] 第2轮输出
[1, 3, 2, 4, 5, 6, 7, 8, 9] 第3轮输出
[1, 2, 3, 4, 5, 6, 7, 8, 9] 第4轮输出
[1, 2, 3, 4, 5, 6, 7, 8, 9] 第5轮输出
[1, 2, 3, 4, 5, 6, 7, 8, 9] 第6轮输出
[1, 2, 3, 4, 5, 6, 7, 8, 9] 第7轮输出
[1, 2, 3, 4, 5, 6, 7, 8, 9] 第8轮输出

从输出结果可知，该排序从第4轮起就已完成整个序列的排序，后续的排序过程中不再存在后一个元素比前一个元素小的情况。所以，当排序过程中所有的序列中不再存在后一个元素比前一个元素更小的情况时，我们就可以停止排序。所以上述程序改进后为：

def bubble_sort(alist):
    for time in range(len(alist)-1):
        exchange = False
        for j in range(len(alist)-1):
            if alist[j+1]< alist[j]:
                alist[j+1],alist[j]=alist[j],alist[j+1]
                exchange = True
        if not exchange:
            break
        print(alist, '第%d轮输出' % (time+1))

alist = [1,3,6,4,5,2,7,9,8]
bubble_sort(alist)

输出结果为：

[1, 3, 4, 5, 2, 6, 7, 8, 9] 第1轮输出
[1, 3, 4, 2, 5, 6, 7, 8, 9] 第2轮输出
[1, 3, 2, 4, 5, 6, 7, 8, 9] 第3轮输出
[1, 2, 3, 4, 5, 6, 7, 8, 9] 第4轮输出

【复杂度分析】$O(n^2)$。

2. 选择排序

【原理】每次选择未进行排序的序列中最小的元素，逐个放在序列的前面。
【排序操作】新建一个列表用于存储选出的元素。循环遍历待排序的列表，每次循环都找出一个列表中的最小元素，将该元素添加到新的列表中，然后将此元素从待排序的列表中删除。

def select_sort(alist):
    new_alist = []
    for i in range(len(alist)):
        mins = min(alist)
        new_alist.append(mins)
        alist.remove(mins)
    print(new_alist)

alist = [1,3,6,4,5,2,7,9,8]
select_sort(alist)

输出结果为：

[1, 2, 3, 4, 5, 6, 7, 8, 9]

【缺点分析】该排序过程中开辟了新的内存空间，所以增加了空间复杂度。同时min()函数与remove()函数的使用，其时间复杂度都为$n$,故而该算法的总体复杂度。
针对重新开辟空间这一点的改善思路步骤为：
将序列从前往后依次将元素设置为最小的那一个，从被设置的元素往后依次遍历查找最小的元素，然后将查找到的最小元素与当前被设定的元素互换位置。

def select_sort(alist):
    for i in range(len(alist)-1):
        min_index = i
        for j in range(i+1, len(alist)):
            if alist[j] < alist[i]:
                min_index = j
        alist[min_index], alist[i] = alist[i], alist[min_index]
        print(alist, '第{0}轮输出'.format(i+1))
        
alist = [1,3,6,4,5,2,7,9,8]
select_sort(alist)

输出结果为：

[1, 3, 6, 4, 5, 2, 7, 9, 8] 第1轮输出
[1, 2, 6, 4, 5, 3, 7, 9, 8] 第2轮输出
[1, 2, 3, 4, 5, 6, 7, 9, 8] 第3轮输出
[1, 2, 3, 4, 5, 6, 7, 9, 8] 第4轮输出
[1, 2, 3, 4, 5, 6, 7, 9, 8] 第5轮输出
[1, 2, 3, 4, 5, 6, 7, 9, 8] 第6轮输出
[1, 2, 3, 4, 5, 6, 7, 9, 8] 第7轮输出
[1, 2, 3, 4, 5, 6, 7, 8, 9] 第8轮输出

【缺点分析】如果所设定元素本身就在排序结束后的位置，那在本次循环中不进行任何操作，相当于程序白跑一回如上第4,5,6,7 轮操作。

3. 插入排序

【原理】从序列的第二个元素开始依次遍历整个序列，固定当前被遍历的对象，比较其与其位置左边所有的对象，若有对象比当前固定的对象大，则将该对象后移，直到被固定的对象左边的所有元素都比所固定的对象小为止。
【排序操作】首先从序列左边第二个元素起依次被固定，将被固定的对象依次与其左边的对象比较，若其左边对象比固定的对象大，则将该左边对象后移直至所有左边的元素都比所固定的对象小为止，然后将固定的对象插到移动后的空位。相当于先将一个元素拿出，空出序列的内存，然后移动比这个元素大的其他元素。
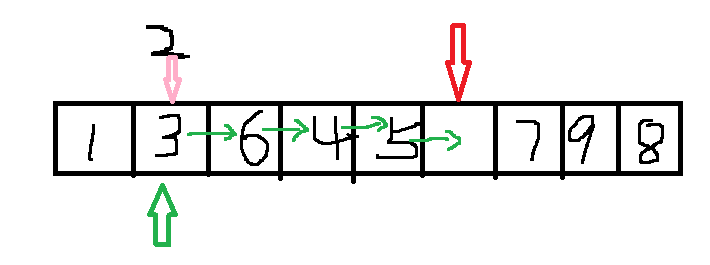
【操作举例】比如原先2在如下图空格位置，我们先将2取出来，空出这个内存位置，然后比较这个空格位置上的左边元素与2的大小关系，其中5比2大，那么将5移到这个空格的位置上，4比2也大，那么将4移到原先5所在的位置上，然后6也比2大，再把6移到原先4所在的位置上，最后3比2也大，所以再移动3到原先6所在的位置上，直到比较1比2小，1保持在原位，那么最后空出这个之前3所在的位置，将2插到这个位置上。这样就完成一轮排序。

def insert_sort(alist):
    for i in range(1,len(alist)):
        temp = alist[i]
        j = i - 1#定位所固定元素的第一个左边位置
        while temp < alist[j] and j >= 0:
            alist[j+1] = alist[j]#元素后移
            j -= 1
        alist[j+1] = temp
        print(alist, '第%d轮输出' % i)

输出结果为：

[1, 3, 6, 4, 5, 2, 7, 9, 8] 第1轮输出
[1, 3, 6, 4, 5, 2, 7, 9, 8] 第2轮输出
[1, 3, 4, 6, 5, 2, 7, 9, 8] 第3轮输出
[1, 3, 4, 5, 6, 2, 7, 9, 8] 第4轮输出
[1, 2, 3, 4, 5, 6, 7, 9, 8] 第5轮输出
[1, 2, 3, 4, 5, 6, 7, 9, 8] 第6轮输出
[1, 2, 3, 4, 5, 6, 7, 9, 8] 第7轮输出
[1, 2, 3, 4, 5, 6, 7, 8, 9] 第8轮输出

4. 快速排序

【原理】首先我们找一个基准数固定，将序列中所有比该基准数小的数都放到该基准数的左侧，将序列中所有比该基准数大的数都放在该基准数的右侧。然后不断左侧递归前述操作，不断右侧递归前述操作。
【排序操作】具体图解可参阅 参考文献2

1. 首先选择一个基准数固定，一般我们选序列中的第一个元素。将该元素取出固定，此时产生“空缺位置1号”。
2. 从序列的右边找第一个比所固定的数小的数，将这个数放在“空缺位置1号”上。此时在该位置上产生“空缺位置2号”。
3. 从左侧，即所固定位置的后一个元素位置起找第一个比所固定的数大的数，将这个数放在“空缺位置2号”上。
4. 循环执行上述1，2，3步骤操作，直到序列的前半侧都是比基准数小的数，后半侧都是比基准数大的数，此时小数与大数中间会产生“空缺位置3”，
5. 将我们所选的基准数放在“空缺位置3上”，这样就完成一次排序。
6. 将左侧小于基准数的所有元素看做一个子序列，递归执行1，2，3，4，5步骤的操作。
7. 将右侧大于基准数的所有元素看做一个子序列，递归执行1，2，3，4，5步骤的操作。

【python 代码】

def partition(alist, left, right):
    temp = alist[left]
    while left < right:
        while left < right and alist[right] >= temp:#从右往左找第一个小于目标元素的元素的索引
            right -= 1
        alist[left] = alist[right]#找到后放到基准数所在的位置上
        while left < right and alist[left] <= temp:
            left += 1
        alist[right] = alist[left]
    alist[left] = temp
    return left
def quick_sort(alist, left, right):
    if left < right:
        mid = partition(alist, left, right)
        quick_sort(alist, left, mid-1)
        quick_sort(alist, mid + 1, right)
    print(alist)

alist = [1,3,6,4,5,2,7,9,8]
quick_sort(alist, 0, len(alist)-1)

【时间复杂度】$O(nlogn)$。

参考文献

1. 清华大学博士讲解Python数据结构与算法（完整版）全套100节
2. https://blog.csdn.net/qq_28584889/article/details/88136498

最后

以上就是幽默往事为你收集整理的排序算法----冒泡、选择、插入、快速1.冒泡排序2. 选择排序3. 插入排序4. 快速排序参考文献的全部内容，希望文章能够帮你解决排序算法----冒泡、选择、插入、快速1.冒泡排序2. 选择排序3. 插入排序4. 快速排序参考文献所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。