快速傅里叶变换FFT进行频谱分析（matlab）快速傅里叶变换FFT进行频谱分析（matlab）

72 阅读 0 评论 48 点赞

我是靠谱客的博主外向荷花，最近开发中收集的这篇文章主要介绍快速傅里叶变换FFT进行频谱分析（matlab）快速傅里叶变换FFT进行频谱分析（matlab），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

快速傅里叶变换FFT进行频谱分析（matlab）

本章摘要：FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。本章主要讲解如何采用matlab进行傅里叶变换，以及需要注意的事项。

一、组合信号

比如有这样一个组合信号，其波形图如下，杂乱无章，看不出名堂。
S=2+3 * cos (2 * pi * 50 * t - pi * 30/180) + 1.5 * cos(2 * pi * 75* t + pi * 90/180)。
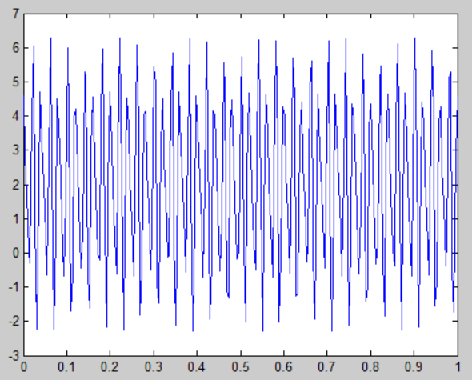
在这里插入图片描述

二、频谱分析

上面的信号波形图杂乱无章，我们可不可以将其频率进行提取了，提取各个信号分量的频率、幅值、相位。答案是可以的，那就是傅里叶变换FFT。下面直接给出结果看看效果，是不是提取出了信号分量的两个频率50Hz, 75Hz，还有它们对应的幅值3，1.5。

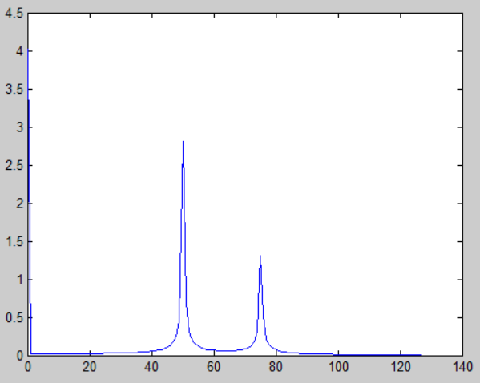
在这里插入图片描述

三、快速傅里叶变换FFT

下面给出了，达到上面结果的FFT变换matlab代码。

t=0:1/256:1;        %采样步长
y= 2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180);
N=length(t);        %样点个数
plot(t,y);
fs=256;             %采样频率
df=fs/(N-1);        %分辨率
f=(0:N-1)*df;       %其中每点的频率
Y=fft(y(1:N))/N*2;  %真实的幅值
%Y=fftshift(Y);
figure(2)
plot(f(1:N/2),abs(Y(1:N/2)));

关于上面代码中的一些参数说明：

经过ADC采样之后，就变成了数字信号。采样定理告诉我们，采样频率要大于信号频率的两倍。 假设采样频率为Fs，信号频率为F，那就因该Fs > 2F。
采样得到的数字信号，就可以做FFT变换了。N个采样点，经过FFT之后，就可以得到N个点的FFT结果。结果结果是左右对称的，所以上面图中的结果只取了一半 256/2=128。为了方便进行FFT运算，通常N取2的整数次方。
分辨率：例如某点n所表示的频率为：Fn=(n-1)*Fs/N。则Fn所能分辨到频率为Fs / N。如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。
幅值：那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率值下的幅度特性。

比如上面峰值处对应的复数表示：
1点： 512+0i
51点：332.55 - 192i
76点：3.4315E-12 + 192i
对应模值分别为：
1点：512
51点：384
76点：192
通过模值可以看出：第一点直流分量的模值512，真实模值2，之间的关系为：512/(N=256）=2
其它两点，384/(N/2)=3，192/(N/2)=1.5。

相位角：直流信号没有相位可言，不用管它。50Hz信号的相位，atan2(-192,332.55)=-0.5236弧度，换算为角度就是180*(-0.5236)/pi=-30.0001。再计算75Hz信号的相位 atan2192,3.4315E-12)=1.5708弧度，换算成角度就是180*1.5708/pi=90.0002。