FFT运算的加深理解——频谱泄露

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

还是接上一篇的例子，为了更好地描述，我们将其表示的物理意义添加上：

N FFT计算点数 8
Fs 采样率 8Hz
fi1 点频频率 1Hz
而且我们一般习惯于0频为中心位置,因此程序修改为这样

N = 8
fs = 8;
fi1 = 1;
 
N = 8
fs = 8;
fi1 = 1;
fcarr = 1*exp(j*2*pi*fi1/fs*[0:N-1]);

x_fft1 = fft(fcarr)/N;

 stem([-4:3],abs(x_fft1))

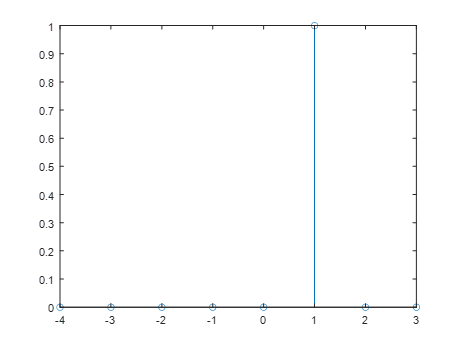
这个图表示在1Hz处有一个幅度为1的点频

还有一个FFT分辨范围和分辨率的概念。
FFT的分辨范围是±fs/2内 。例如这里就是[-4,4)，

FFT的分辨率，是采样点总时间的倒数。例如这里，采样率是8Hz，点数是8个点，那么FFT的运算时间就是1s，1s的倒数就是1Hz。

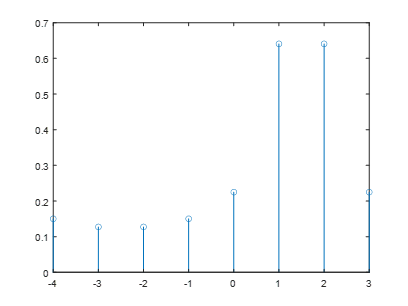
我们将fi1 = 1.5;
一下子，所有的频率点都有幅值了，这就是频谱泄露。原本本该X=1.5Hz处有一条为1的幅值线变成了X = 2Hz处的幅值变成了0.64，且X=3Hz处的幅值也是0.64，这就是1.5Hz的幅值泄露到其他频率上去了，导致看起来其他频率都有信号一样，造成了分析的失真。

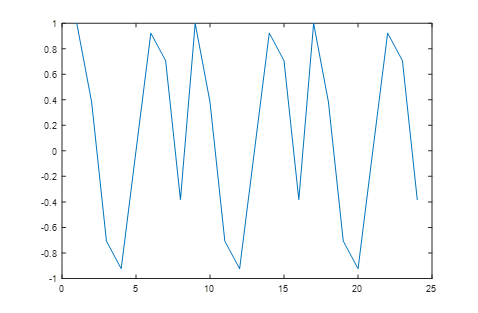
（1）从信号连续性的角度来看，因为FFT运算是假设截取的信号是周期的，信号进行周期拓展之后会导致相位不连续，这样就会导致其他频率出现了

（2）完全从 数学表达式来看

看W的定义：

W =  [exp(-j*2*pi/8*0),exp(-j*2*pi/8*1),exp(-j*2*pi/8*2),exp(-j*2*pi/8*3),exp(-j*2*pi/8*4),exp(-j*2*pi/8*5),exp(-j*2*pi/8*6),exp(-j*2*pi/8*7)]

可以看出
点频频率只能是1,2,3,4,5,6,7（或者1,2,3，-4，-3，-2,-1）才能完全与W正交，不是这些数计算肯定会有残留值。其他频率就会有残留值出现。

根据上面分析，除了点频是1,2,3，-4，-3，-2,-1Hz，其他频率必然会出现频谱泄露，导致幅值的失真。

失真最大的时候也就处于两个分辨频率的中间点，例如1Hz,2Hz中间点1.5Hz。
幅度只有正确的0.64。当点频为1.1Hz时，幅度为0.984。

整个频率区间[-4:3]Hz内，FFT幅度的变化

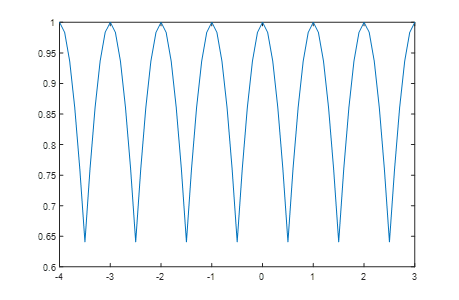
用功率来表征的话，最多下降快4dB了

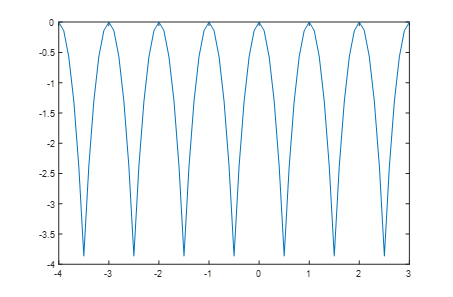
频谱泄露会严重影响对频率的分析结果
1、 幅值变的比实际的低
2、 频率分析不准

但频谱泄露后，当前频率表征的幅度降低，但FFT表征的总功率并没有降低。
所有谱线的总功率和还是等于1

最后

以上就是落寞荔枝为你收集整理的FFT运算的加深理解——频谱泄露的全部内容，希望文章能够帮你解决FFT运算的加深理解——频谱泄露所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。