借matlab仿真说明栅栏效应借matlab仿真说明栅栏效应

66 阅读 0 评论 44 点赞

我是靠谱客的博主细腻豌豆，最近开发中收集的这篇文章主要介绍借matlab仿真说明栅栏效应借matlab仿真说明栅栏效应，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

借matlab仿真说明栅栏效应

1.栅栏效应的原因

由于数字采样的不连续性，无论是时域采样还是频域采样，都像透过栅栏观察，采样的点就是只能看到栅栏缝隙的部分，其余信号部分视为0。

2.栅栏效应的后果

如果两个采样点之间相隔较大的话也许会将一些中间的信息丢失掉（无论时域还是频域）。

3.matlab仿真说明栅栏效应

3.1时域栅栏效应

clear all;
close all;

f=10;%信号频率
k=30;
fs=k*f;%采样频率
N=1000;%信号长度/采样点数
n=[0:1:N-1];
x=n/fs;%时域横坐标

y=sin(2*pi*f*x);%信号
figure
plot(x,y);
xlim([0,0.1]);
figure
stem(x,y);
xlim([0,0.1]);

用matlab的两个画图函数plot和stem对比更能有效理解栅栏效应。
stem完全体现了采样这个过程：
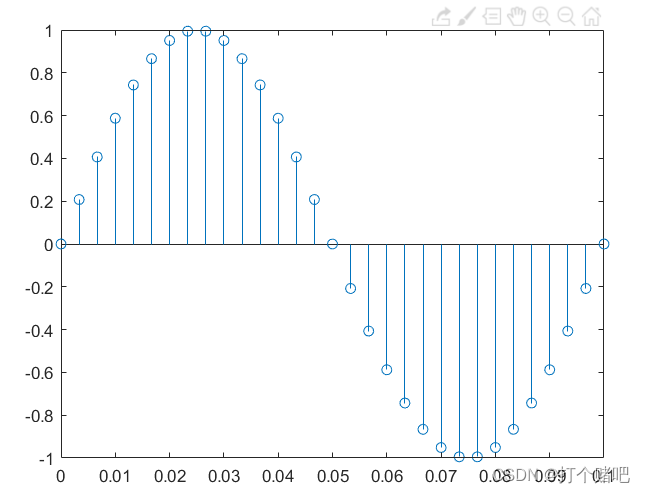
在这里插入图片描述
每一条线就是一次采样，这些圆点也就是我们能从栅栏缝隙中看到的信号部分。
plot则像是用采样的这些点将数字信号还原成连续信号：

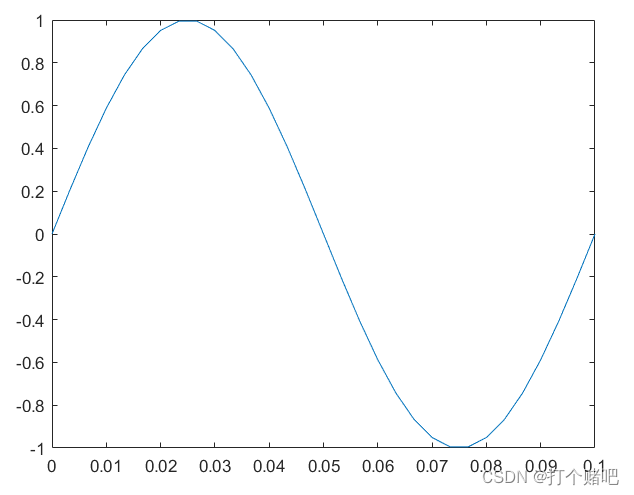
上述采样图是采样率为信号频率的30倍时的结果。观察到丢失的部分信息中包含sin函数最高点和最低点。
这就是栅栏效应造成的时域偏差

3.2频域

clear all;
close all;

f=10;%信号频率
k=30;
fs=k*f;%采样频率
N=1000;%信号长度/采样点数
caiyangzhouqishu=N/k;%看拼音，采样周期数
n=[0:1:N-1];
x=n/fs;%时域横坐标

y=sin(2*pi*f*x);
figure
plot(x,y);
xlim([0,0.1]);
figure
stem(x,y);
xlim([0,0.1]);
y_fft=fftshift(fft(y,N));
x_f=[-N/2:1:N/2-1];
x_f=x_f/N*fs;%频域横坐标
figure
plot(x_f,abs(y_fft));%双边频谱图
title("信号原频谱");
figure
stem(x_f,abs(y_fft));%双边频谱图
title("信号原频谱");

同样用plot和stem分别画出频谱图。
plot图：
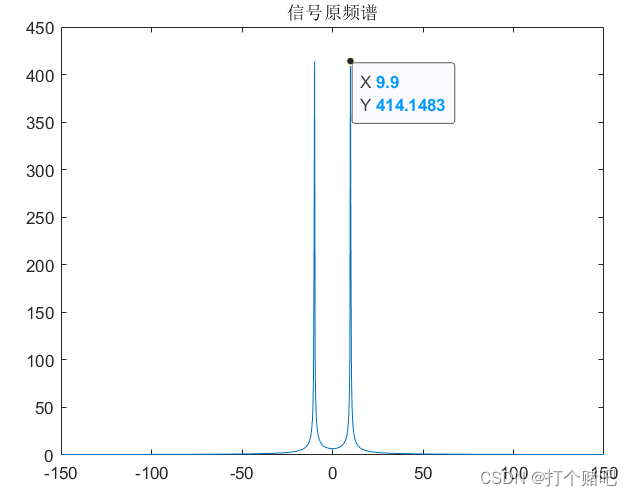
在这里插入图片描述
峰值所在的频率是9.9Hz，与设置的10Hz频率有偏差，这是因为频域同样有采样点，采样点的个数就是作fft的点数（fft(y,N)）。因为此时10Hz处没有采样点，类似于被栅栏挡住了，用stem作图放大10Hz处的频谱图也可以看出：
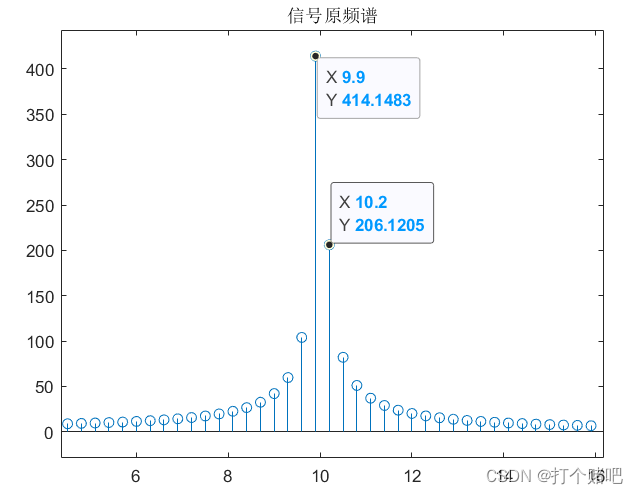
在这里插入图片描述
因此峰值取在最靠近10Hz的采样点（9.9Hz）处。实际的峰值应处在10Hz处，且高度必定比9.9Hz高。
这就是栅栏效应造成的频域偏差。

4.栅栏效应的解决办法——补零

补零是针对于频域栅栏效应的解决办法，其本质是增加频域的采样点，相当于让栅栏缝隙变密，这样采样点更密集，漏掉的信息会减少。

5.matlab补零处理

clear all;
close all;

f=10;%信号频率
k=30;
fs=k*f;%采样频率
N=1000;%信号长度/采样点数
caiyangzhouqishu=N/k;%看拼音，采样周期数
n=[0:1:N-1];
x=n/fs;%时域横坐标

y=sin(2*pi*f*x);
figure
plot(x,y);
xlim([0,0.1]);
figure
stem(x,y);
xlim([0,0.1]);
y_fft=fftshift(fft(y,N));
x_f=[-N/2:1:N/2-1];
x_f=x_f/N*fs;%频域横坐标
figure
plot(x_f,abs(y_fft));%双边频谱图
title("信号原频谱");
figure
stem(x_f,abs(y_fft));%双边频谱图
title("信号原频谱");

%% 补零
Nfft = 10000;
y0_fft=fftshift(fft(y,Nfft));
x0_f=[-Nfft/2:1:Nfft/2-1];
x0_f=x0_f/Nfft*fs;
figure
plot(x0_f,abs(y0_fft));
title("信号补零频谱");
figure
plot(x_f,abs(y_fft));
hold on;
plot(x0_f,abs(y0_fft),"-r");
xlim([5,15]);
legend("信号原频谱","信号补零频谱");
title("信号原频谱和信号补零频谱");

代码中fft运算的点数由N=1000变成Nfft=10000，频域采样点个数是原来的10倍。
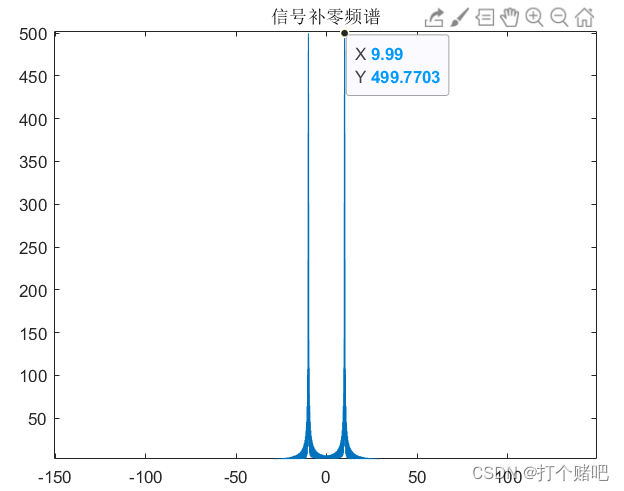
在这里插入图片描述
补零后的频谱峰值所在的频率是9.99Hz，更靠近真实频率10Hz，证明增加采样点数可以有效改善栅栏效应的影响。
只是增加点数同样增加了运算量，实际处理中不能一昧追求精度增加补零个数，会均衡考虑运算量和精度。