数字信号处理的栅栏效应和时域补零

81 阅读 0 评论 54 点赞

我是靠谱客的博主精明手链，最近开发中收集的这篇文章主要介绍数字信号处理的栅栏效应和时域补零，觉得挺不错的，现在分享给大家，希望可以做个参考。

根据我上篇转载的文章，我又继续翻了翻《数字信号处理》，对离散信号的DFT又有了进一步的了解。以前在考试后就把书本上的内容扔掉了，现在用到它的时候还得重新学习一遍....

下面是数字信号处理中困扰我很久的：栅栏效应和时域补零。

因为DFT或者（FFT）计算的只是离散点上面的频谱，这些离散点是Fs=(n-1)*Fs/N，其中频率的分辨率是dF=Fs/N。所以DFT计算的只是dF整数倍处的频谱，而不是连续频率的函数。这就像在通过一个“栅栏”看景物一样，称为“栅栏效应”。

在做DFT的时候人们常常在有效数据后面补一些零来达到频谱改善的效果，但是这并不会提高频率分辨率，因为补零不会增加有效数据！

但是补零常常有一些好处：

1、可以使数据点数N为2的整数次幂，便于FFT计算；

2、补零使原来的X(k)起到做插值的作用，克服栅栏效应，使谱外观得到平滑。末尾补零，DFT处理的点数大于实际抽样的点数，这样使原来看不见的频谱线能被看到；

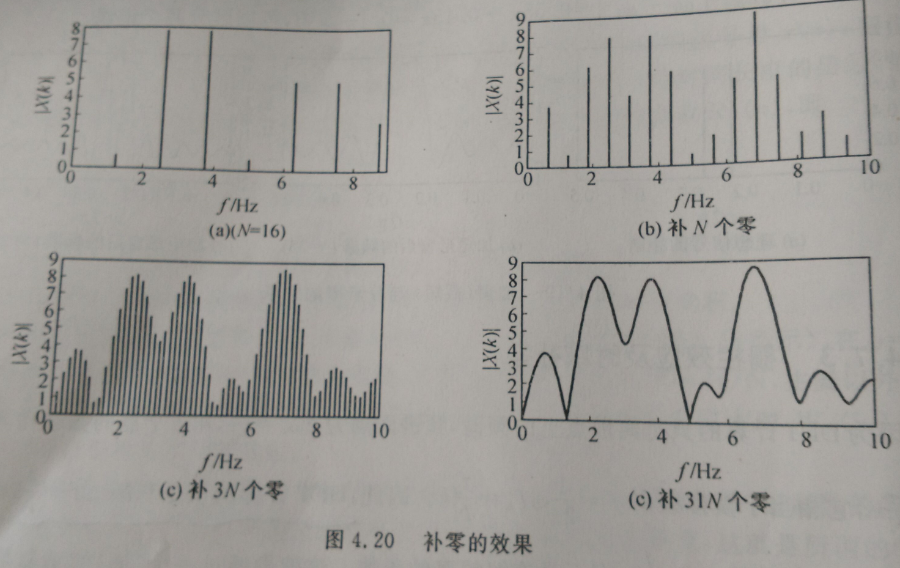
3、由于对数据截断后引起频谱泄露，有可能在频谱中出现一些难以确认的波峰，补零后消除这种现象；

手上还有一个matlab的仿真程序，等找到了再上传吧~

以上就是精明手链为你收集整理的数字信号处理的栅栏效应和时域补零的全部内容，希望文章能够帮你解决数字信号处理的栅栏效应和时域补零所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。