DFT/FFT存在的问题-----栅栏效应(MTALAB仿真演示,看完后会有不少的收获,一定要仔细看下去哟)
下面我们来研究一下DFT/FFT存在的两个重要的问题
1.栅栏效应
2.频谱泄露
1.栅栏效应
说到栅栏效应就要提到两个分辨率,一个是物理分辨率,另外一个是计算分辨率。
假设对一个信号以采样率fs进行采样,采样M个点,做N点FFT变换(N≥M),那么对应的物理分辨率为fs/M,计算分辨率为fs/N,其中物理分辨率是首要解决问题,如果不解决物理分辨率,即使计算分辨率再高计算得到的结果也是错的。
下面通过程序来说明
1. 定义两个余弦信号的幅值分别为A1=2V、A2=1V,f1=4H、f2=4.5Hz
以频率fs=16Hz为采样频率,即每隔1/fs=0.0625s采样一个点,
A=[2,1]; %输入两个信号的幅值
f=[4, 4.5]; %输入两个信号的频率
fs=16; %采样频率: fs Hz
M=16; %采样点数
N=16; %FFT点数 N >= M
%计算分辨率: fs/M
%物理分辨率: fs/N
fprintf("物理分辨率:%f Hzn",fs/M)
fprintf("计算分辨率:%f Hzn",fs/N)
此时可以得到两个采样率

首先,来分析一下物理分辨率,这个分辨率代表能采样到的实际信号的频率,即采样的间隔是1Hz,意思是从0开始,每个1Hz采样一个频率,分别可以采到:0Hz、1Hz、2Hz、3Hz、4Hz…
再来分析一下计算分辨率(1Hz),这个分辨率决定了计算出的信号之间的频率间隔,也就是计算可以得到的信号的频率分量,计算的结果可以有:0Hz、1Hz、2Hz、3Hz、4Hz…
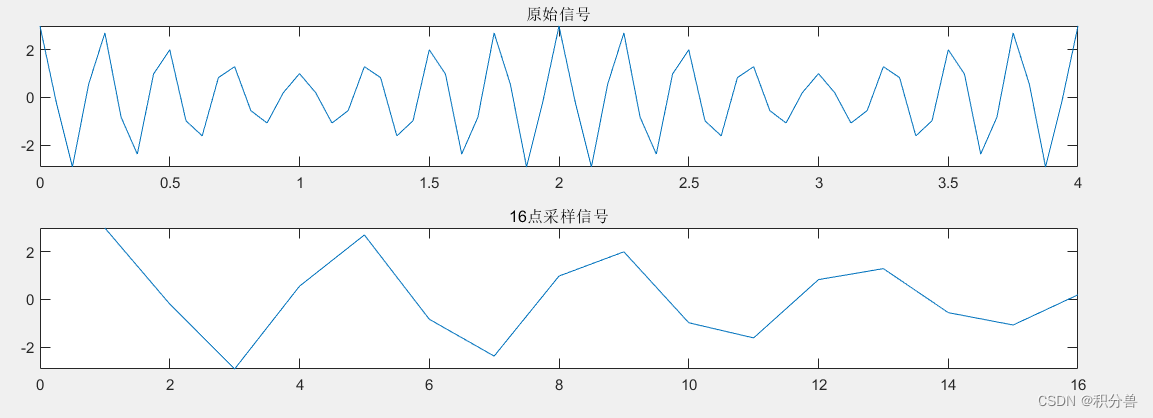
2.生成一段长的采样信号,从第一个点开始截取信号上的M个点
%生成一段长的采样信号
t=(0:4*M)/fs; % 序列有4N个点,每两个点的间隔为1/fs
sigal=A(1)*cos(2*pi*f(1)*t)+A(2)*cos(2*pi*f(2)*t);
figure(1);
subplot(311);plot(t, sigal);%原始信号
title('原始信号');
%截取signal信号上M点
n_Start = 1;
n_End=n_Start+M-1; %取从n_Start开始往后的N_FFT个点
sample_signal=sigal(n_Start:n_End); %获取取M点长的信号
figure(1);
subplot(312);plot(sample_signal); %待分析信号
title([int2str(M),'点采样信号']);
下面是分别得到的两个信号
3.对M点采样信号进行N点FFT处理
%-----------------------------信号处理-------------------------------------
%FFT分析
% sig_fft=my_fft(sig_sample,N); %N点FFT分析(自编FFT)
s_fft=fft(sample_signal,N); %对采样信号做N点FFT分析(内置FFT)
fn=fs*(0:N/2)/N; %FFT变换后的每个点代表的实际频率
%求信号的实际幅值,取前N/2+1个点即可,后面的点关于N/2+1对称(除直流)`
%FFT后的N个点: 1 2 3 ... N/2 N/2+1 N/2+2 ... N-1 N
%每点实际频率: 0 fs/N 2fs/N ... (N/2-1)fs/N fs/2 (N/2-1)fs/N 2fs/N fs/N
sig_fft_amp=abs(s_fft(1:N/2+1))/N; %取前N/2+1点,即0-fs的频率对应的幅值
%除直流和fs/2外的其他频率分量关于N/2+1点对称平分,因此需要乘以2恢复
sig_fft_amp(2:end-1)=sig_fft_amp(2:end-1)*2;
figure(2);subplot(211);
stem(fn,sig_fft_amp);title('直接FFT后的频谱');
xlabel('频率/Hz');ylabel('幅度/V');
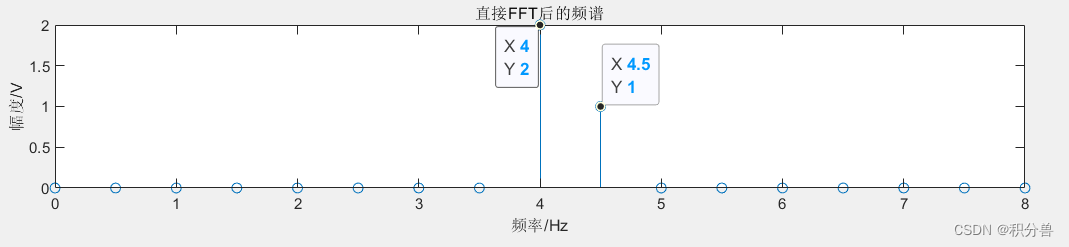
16点采样信号16点FFT分析结果:
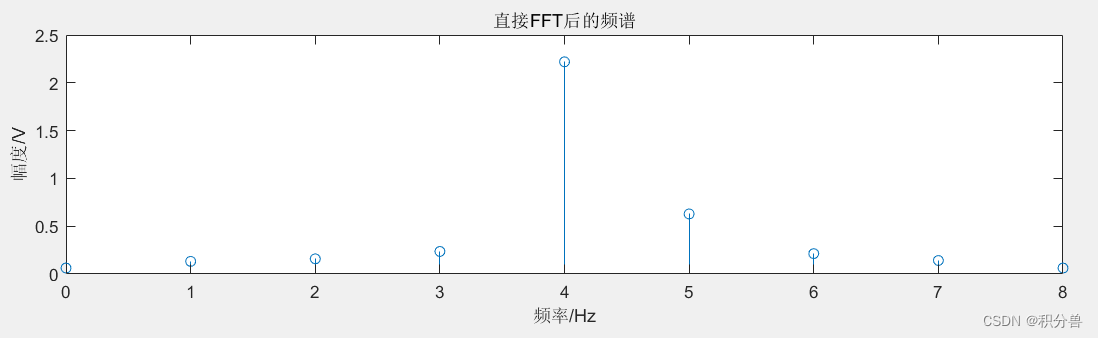
从上图我们可以观察到分别从0HZ到8Hz,其中间隔为1Hz,这个间隔就是我们所说的计算分辨率。但是未得到我们设定的4.5Hz。这种现象就是我们所说的栅栏效应
(1) 接着往下研究,我们可以知道16点FFT的计算分辨率只有fs/N=16Hz/16=1Hz,似乎好像是因为计算分辨率的不够而没有得到4.5Hz的信号,下面我们提高计算分辨率来研究一下是否是由于计算分辨率不够而造4.5Hz的频率提取失败的,现在我们将N=16点的FFT改为N=32点的FFT重新计算一下结果(只修改N=32)(注释:分辨率越高对应的值越小)
A=[2,1]; %输入两个信号的幅值
f=[4, 4.5]; %输入两个信号的频率
fs=16; %采样频率: fs Hz
M=16; %采样点数
N=32; %FFT点数 N >= M
%计算分辨率: fs/M
%物理分辨率: fs/N
fprintf("物理分辨率:%f Hzn",fs/M)
fprintf("计算分辨率:%f Hzn",fs/N)
现在的分辨率如下:计算分辨率率已经提高到0.5Hz
物理分辨率决定能采到的信号的频率:0Hz、1Hz、2Hz、3Hz、4Hz…
计算分辨率决定FFT能计算出来的频率:0Hz、0.5Hz、1Hz、1.5Hz、2Hz、2.5Hz、3Hz、3.5Hz、4Hz…

16点采样信号32点FFT分析结果
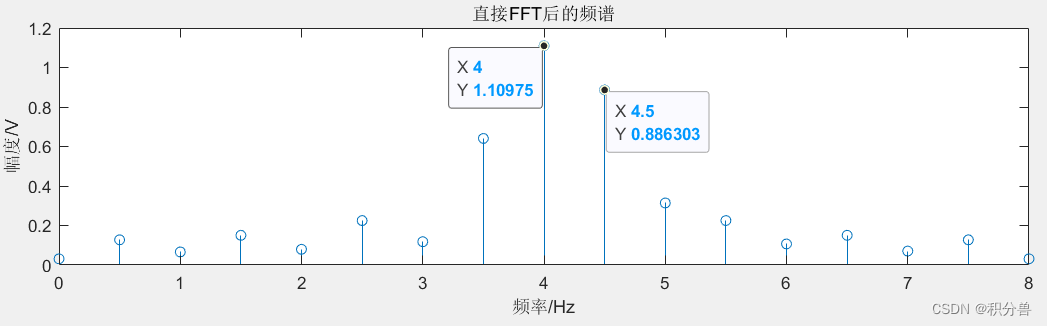
观察上图,我们发现好像是找到了4.5Hz的信号,但是我们可以观察一下两个信号的幅值之比基本不满足A2/A1等于我们原来设定的1/2,因此我们可以判断这个结果肯定是不正确的。其实,也可以这样理解,物理分辨率代表能能采到的实际的信号(1Hz的物理分辨率可以采到:0Hz、1Hz、2Hz、3Hz、4Hz…),N点FFT是基于已经采到的信号进行分析处理的,所以计算分辨率(fs/N)可以说成是基于物理分辨率之上的,虽然我们提高了计算分辨率(即在图上显示的结果更加的密集),但是物理分辨率却已经决定了某些信号的频率不能采到,那么计算得到的这些不能采到的频率结果肯定也是不对的。所以可以得到一个结论:
只是提高FFT运算的点数,即物理分辨率,并不能解决提取信号频率的问题。
(2) 通过测试提高完计算分辨率并不能解决我们的问题,下面我们尝试从提高物理分辨率的手段来研究问题。
我们先单纯提高物理分辨率,而不改变计算分辨率,来观察一下结果
A=[2,1]; %输入两个信号的幅值
f=[4, 4.5]; %输入两个信号的频率
fs=16; %采样频率: fs Hz
M=32; %采样点数
N=16; %FFT点数 N >= M
%计算分辨率: fs/M
%物理分辨率: fs/N
fprintf("物理分辨率:%f Hzn",fs/M)
fprintf("计算分辨率:%f Hzn",fs/N)
只提高物理分辨率到0.5Hz
物理分辨率决定能采到的信号的频率:0Hz、0.5Hz、1Hz、1.5Hz、2Hz、2.5Hz、3Hz、3.5Hz、4Hz…
计算分辨率决定FFT能计算出来的频率:0Hz、1Hz、2Hz、3Hz、4Hz…

32点采样信号16点FFT计算结果
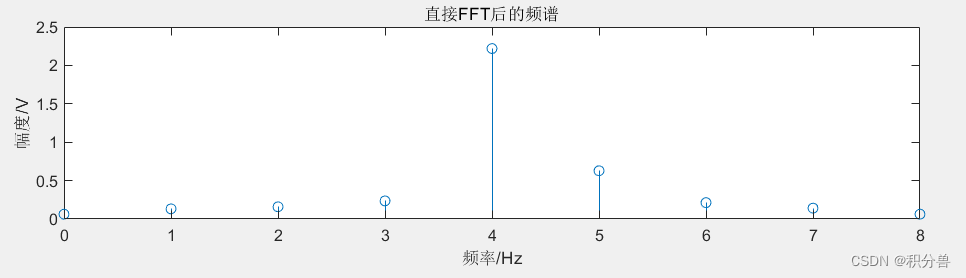
可以观察到,只提高物理分辨率,而不提高计算分辨率出现了上面这样的问题,FFT计算的结果间隔为fs/N=1Hz(即图上显示的频率间隔也只有1Hz),因此,只提高物理分辨率,也就是当计算分辨率小于物理分辨率时没有意义,不能完全体现出物理分辨率提高后的效果。
(3)现在我们在提高物理分辨率的基础上,同时提高计算分辨率
A=[2,1]; %输入两个信号的幅值
f=[4, 4.5]; %输入两个信号的频率
fs=16; %采样频率: fs Hz
M=32; %采样点数
N=32; %FFT点数 N >= M
%计算分辨率: fs/M
%物理分辨率: fs/N
fprintf("物理分辨率:%f Hzn",fs/M)
fprintf("计算分辨率:%f Hzn",fs/N)
现在物理分辨率和计算分辨率均提高到了0.5Hz
物理分辨率决定能采到的信号的频率:0Hz、0.5Hz、1Hz、1.5Hz、2Hz、2.5Hz、3Hz、3.5Hz、4Hz…
计算分辨率决定FFT能计算出来的频率:0Hz、0.5Hz、1Hz、1.5Hz、2Hz、2.5Hz、3Hz、3.5Hz、4Hz…

32点采样信号32点FFT计算得到的结果
观察上图,可以发现计算结果正确,正确的采到了4Hz和4.5Hz的信号,并且二者的幅值之比满足理论设定的比值。因此,如果我们想要消除栅栏效应,只是提高计算分辨率是不行的,同时需要提高物理分辨率(这里的采样频率是固定的,是为了和单片机的运算相符合,因为单片机实现FFT的时候,一般是固定了512或者1024点,然后改变采样频率的,最后通过这些点数来得到我们的FFT计算结果)
其实,我们可以继续往下研究一下,当我们设置的物理分辨率已经可以分辨出我们给定的信号的时候,那么我再提高计算分辨率会产生什么样的结果?此时是否又多出了新的频率分量?此时的4Hz和4.5Hz的信号是否还能计算出来,它们的幅值比例又是多少,是否还满足理论之比?(可以设置 M=32,N=64来观察一下结果,或者其他值也是可以的,不过要先满足物理分辨率能采到我们需要的信号基础上,不然研究是没有意义的)
完整代码:
clc;clear;close all;
A=[2,1]; %输入两个信号的幅值
f=[4, 4.5]; %输入两个信号的频率
fs=16; %采样频率: fs_n Hz
M=32; %采样点数
N=64; %FFT点数 N >= M
%计算分辨率: fs/M
%物理分辨率: fs/N
fprintf("物理分辨率:%f Hzn",fs/M)
fprintf("计算分辨率:%f Hzn",fs/N)
%生成一段长的采样信号
t=(0:4*M)/fs; % 序列有4N个点,每两个点的间隔为1/fs
sigal=A(1)*cos(2*pi*f(1)*t)+A(2)*cos(2*pi*f(2)*t);
figure(1);
subplot(311);plot(t, sigal);%原始信号
title('原始信号');
%随机截取signal信号上M点
% n_Start=randperm(M,1); %从1-M随机获取一个数,作为起始点
n_Start = 1;
n_End=n_Start+M-1; %取从n_Start开始往后的N_FFT个点
sample_signal=sigal(n_Start:n_End); %获取取M点长的信号
figure(1);
subplot(312);plot(sample_signal); %待分析信号
title([int2str(M),'点采样信号']);
%-----------------------------信号处理-------------------------------------
%FFT分析
% sig_fft=my_fft(sig_sample,N); %N点FFT分析(自编FFT)
s_fft=fft(sample_signal,N); %对采样信号做N点FFT分析(内置FFT)
fn=fs*(0:N/2)/N; %FFT变换后的每个点代表的实际频率
%求信号的实际幅值,取前N/2+1个点即可,后面的点关于N/2+1对称(除直流)`
%FFT后的N个点: 1 2 3 ... N/2 N/2+1 N/2+2 ... N-1 N
%每点实际频率: 0 fs/N 2fs/N ... (N/2-1)fs/N fs/2 (N/2-1)fs/N 2fs/N fs/N
sig_fft_amp=abs(s_fft(1:N/2+1))/N; %取前N/2+1点,即0-fs的频率对应的幅值
%除直流和fs/2外的其他频率分量关于N/2+1点对称平分,因此需要乘以2恢复
sig_fft_amp(2:end-1)=sig_fft_amp(2:end-1)*2;
figure(2);subplot(211);
stem(fn,sig_fft_amp);title('直接FFT后的频谱');
xlabel('频率/Hz');ylabel('幅度/V');
接下来有时间的时候会继续更新频谱泄露和加窗改善的问题。
最后
以上就是唠叨金鱼最近收集整理的关于【DFT/FFT存在的问题---栅栏效应的解决手段】DFT/FFT存在的问题-----栅栏效应(MTALAB仿真演示,看完后会有不少的收获,一定要仔细看下去哟)的全部内容,更多相关【DFT/FFT存在内容请搜索靠谱客的其他文章。








发表评论 取消回复