视觉SLAM学习笔记3——eigen库的基础编程一、头文件二、矩阵与向量的定义三、矩阵的输入与输出四、矩阵的加减乘除五、随机数、数乘、转置、行列式、逆等六、特征值与特征向量七、解方程八、矩阵的角操作九、均值、求和、最值、迹等

101 阅读 0 评论 67 点赞

我是靠谱客的博主陶醉月光，最近开发中收集的这篇文章主要介绍视觉SLAM学习笔记3——eigen库的基础编程一、头文件二、矩阵与向量的定义三、矩阵的输入与输出四、矩阵的加减乘除五、随机数、数乘、转置、行列式、逆等六、特征值与特征向量七、解方程八、矩阵的角操作九、均值、求和、最值、迹等，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

一、头文件

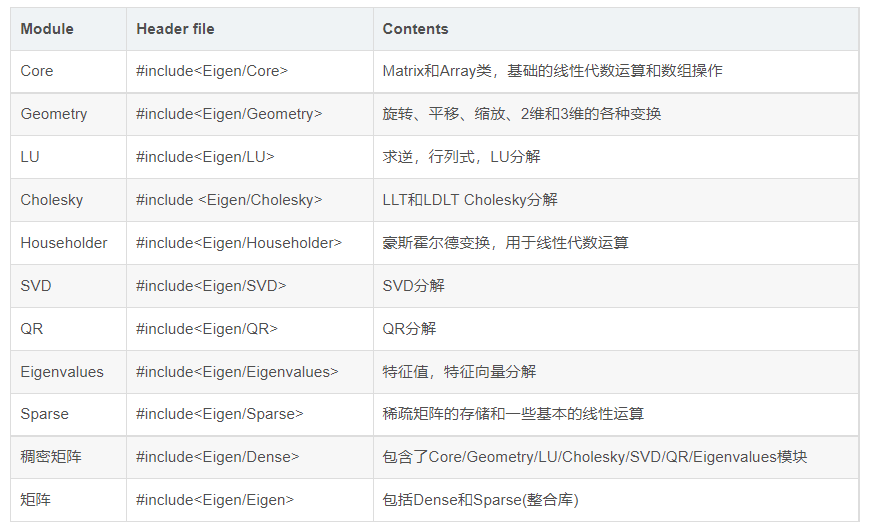
一般情况下，只需要：

#include <Eigen/Core>
#include <Eigen/Dense>

二、矩阵与向量的定义

Eigen 中所有向量和矩阵都是Eigen::Matrix，它是一个模板类。

它的前三个参数为：数据类型，行，列。

// 声明一个2*3的float矩阵
 Eigen::Matrix<float, 2, 3> matrix_23;
//声明一个5*1的double向量
Eigen::Matrix<double, 5, 1> matrix_51;

后面的名称为变量名，按自己习惯定义即可。

同时，Eigen 通过 typedef 提供了许多内置类型，不过底层仍是Eigen::Matrix，比如以下两种d定义向量的方式是一样的：

Eigen::Matrix<double, 3, 1>  v_3d;  //即三维double向量
Eigen::Vector3d v_3d;

以下两种定义3*3方阵的方式也是一定的：

Eigen::Matrix<double, 3, 3> matrix_33 ;
Eigen::Matrix3d matrix_33 ;

初始化为0：

matrix_33 = Eigen::Matrix3d::Zero();

若不确定矩阵大小，可以使用动态大小的矩阵：

Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > matrix_dynamic;
// 更简单的
Eigen::MatrixXd matrix_x;

三、矩阵的输入与输出

例如定义2*3矩阵：

 Eigen::Matrix<float, 2, 3> matrix_23;

矩阵初始化（输入）：

matrix_23 << 1, 2, 3, 4, 5, 6;

矩阵显示（输出）：

 cout << matrix_23 << endl;

1 2 3
4 5 6

与matlab类似，可以用括号访问矩阵中的元素：

 for (int i=0; i<2; i++) 
    {
        for (int j=0; j<3; j++)
            cout<<matrix_23(i,j)<<"t";
        cout<<endl;
    }

1 2 3
4 5 6

也可以基于整行或整列操作：

Eigen::MatrixXf m(3,3);
  m << 1,2,3,
       4,5,6,
       7,8,9;
  cout << "Here is the matrix m:" << endl << m << endl;
  cout << "2nd Row: " << m.row(1) << endl;
  m.col(2) += 3 * m.col(0);
  cout << "After adding 3 times the first column into the third column, the matrix m is:n";
  cout << m << endl;

Here is the matrix m:
1 2 3
4 5 6
7 8 9
2nd Row: 4 5 6
After adding 3 times the first column into the third column, the matrix m is:
 1  2  6
 4  5 18
 7  8 30

四、矩阵的加减乘除

需要注意此类操作数据类型应该一致，矩阵维度也要满足运算要求，以乘法操作为例：

Eigen::Vector3d v_3d;
Eigen::Matrix<float,3,1> vd_3d;
v_3d << 3, 2, 1;
vd_3d << 4,5,6;
Eigen::Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;   //数据类型转换
cout << result << endl;

Eigen::Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;
cout << result2 << endl;

其它四则运算类似，改用+-*/即可。

五、随机数、数乘、转置、行列式、逆等

    matrix_33 = Eigen::Matrix3d::Random();      // 随机数矩阵
    cout << matrix_33 << endl << endl;

    cout << matrix_33.transpose() << endl;      // 转置
    cout << matrix_33.sum() << endl;            // 各元素和
    cout << matrix_33.trace() << endl;          // 迹
    cout << 10*matrix_33 << endl;               // 数乘
    cout << matrix_33.inverse() << endl;        // 逆
    cout << matrix_33.determinant() << endl;    // 行列式

输出为：

0.680375   0.59688 -0.329554
-0.211234  0.823295  0.536459
0.566198 -0.604897 -0.444451

0.680375 -0.211234  0.566198
0.59688  0.823295 -0.604897
-0.329554  0.536459 -0.444451
1.61307
1.05922
6.80375   5.9688 -3.29554
-2.11234  8.23295  5.36459
5.66198 -6.04897 -4.44451
-0.198521   2.22739    2.8357
1.00605 -0.555135  -1.41603
-1.62213   3.59308   3.28973
0.208598

六、特征值与特征向量

// 实对称矩阵可以保证对角化成功
Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> eigen_solver ( matrix_33.transpose()*matrix_33 );
cout << "Eigen values = n" << eigen_solver.eigenvalues() << endl;
cout << "Eigen vectors = n" << eigen_solver.eigenvectors() << endl;

输出：

Eigen values = 
0.0242899
 0.992154
  1.80558
Eigen vectors = 
-0.549013 -0.735943  0.396198
 0.253452 -0.598296 -0.760134
-0.796459  0.316906 -0.514998

七、解方程

求解 matrix_NN * x = v_Nd 这个方程

定义

#define MATRIX_SIZE 5

    Eigen::Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;
    matrix_NN = Eigen::MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );
    Eigen::Matrix< double, MATRIX_SIZE,  1> v_Nd;
    v_Nd = Eigen::MatrixXd::Random( MATRIX_SIZE,1 );

直接求逆求解直接但运算量大：

Eigen::Matrix<double,MATRIX_SIZE,1> x = matrix_NN.inverse()*v_Nd;
cout << "x=" << x <<endl;

x=-0.745267
 -1.09144
-0.737525
 -1.21405
 -1.18348

通常用矩阵分解来求，例如QR分解，速度会快很多：

    x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
	cout << "x=" << x <<endl;

x=-0.745267
 -1.09144
-0.737525
 -1.21405
 -1.18348

运算结果当然是一致的。

八、矩阵的角操作

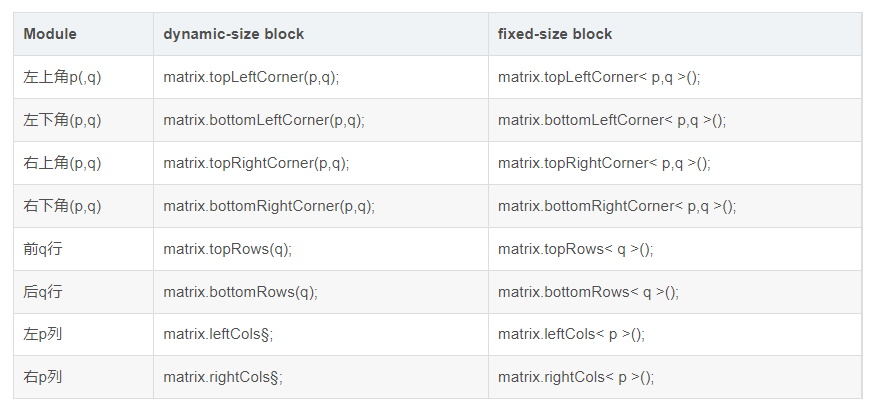
    Eigen::Matrix4f m_44;
  m_44 << 1, 2, 3, 4,
       5, 6, 7, 8,
       9, 10,11,12,
       13,14,15,16;
  cout << "m_44.leftCols(2) =" << endl << m_44.leftCols(2) << endl << endl;
  cout << "m_44.bottomRows<2>() =" << endl << m_44.bottomRows<2>() << endl << endl;
  m_44.topLeftCorner(1,3) = m_44.bottomRightCorner(3,1).transpose();
  cout << "After assignment, m_44 = " << endl << m_44 << endl;

输出为：

m_44.leftCols(2) =
 1  2
 5  6
 9 10
13 14

m_44.bottomRows<2>() =
 9 10 11 12
13 14 15 16

After assignment, m_44 = 
 8 12 16  4
 5  6  7  8
 9 10 11 12
13 14 15 16

九、均值、求和、最值、迹等

Eigen::Matrix2d mat;
  mat << 1, 2,3, 4;
  cout << "Here is mat.sum():       " << mat.sum()       << endl;
  cout << "Here is mat.prod():      " << mat.prod()      << endl;
  cout << "Here is mat.mean():      " << mat.mean()      << endl;
  cout << "Here is mat.minCoeff():  " << mat.minCoeff()  << endl;
  cout << "Here is mat.maxCoeff():  " << mat.maxCoeff()  << endl;
  cout << "Here is mat.trace():     " << mat.trace()     << endl;

输出为：

Here is mat.sum():       10
Here is mat.prod():      24
Here is mat.mean():      2.5
Here is mat.minCoeff():  1
Here is mat.maxCoeff():  4
Here is mat.trace():     5