矩阵对角化
- 1.矩阵对角化(Diagonalizing a Matrix)
- 1.1 对角矩阵的优点
- 1.2 求解一般矩阵的特征值和特征向量
- 1.3 矩阵对角化
- 1.4 计算 <span class="katex--inline">A^k</span>
- 1.5 矩阵对角化的注意事项
1.矩阵对角化(Diagonalizing a Matrix)
笔记参考来源:Visualizing Diagonalization & Eigenbases
1.1 对角矩阵的优点

对角矩阵优点1:
我们观察到对角矩阵只是对标准基进行了缩放,而没有进行旋转(这里的性质和特征向量有些类似!!!)这大大提高了线性变换的确定性(尤其对于高维空间中的线性变换),同时也大大简化了计算量
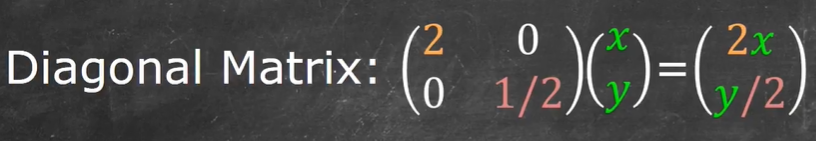
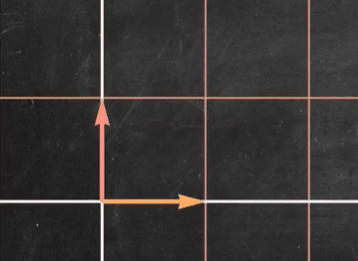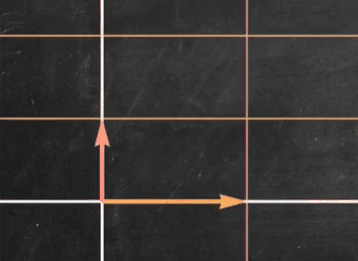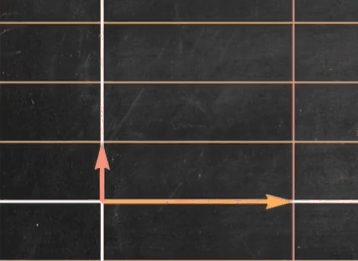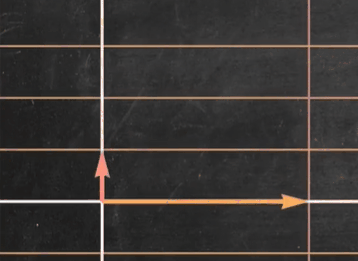
对角矩阵优点2:
特别容易求出对角矩阵的逆矩阵
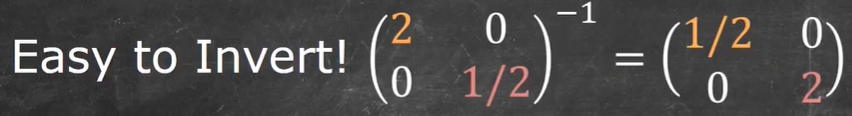
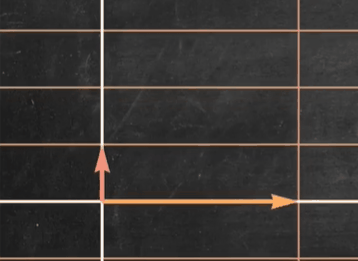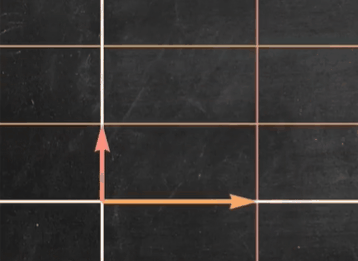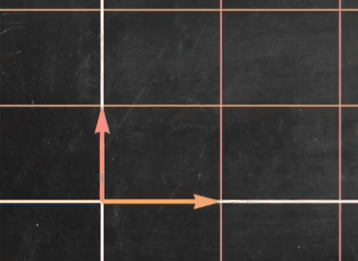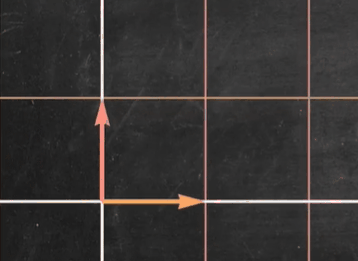
1.2 求解一般矩阵的特征值和特征向量
我们将一般矩阵化为对角矩阵

我们观察到一般矩阵相较于对角矩阵,其线性变换较为复杂
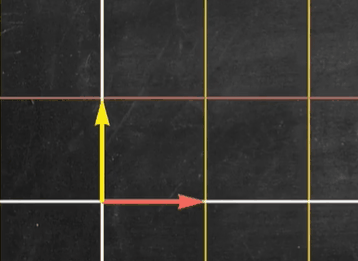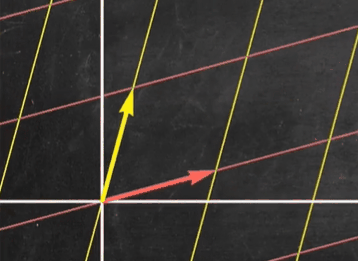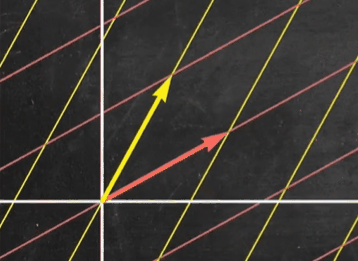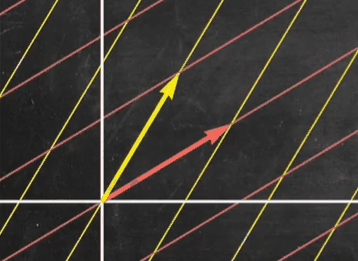
我们求出上述矩阵的特征向量和特征值
求解矩阵的特征向量、特征值
方法一:
A
=
[
5
/
4
3
/
4
3
/
4
5
/
4
]
A
x
⃗
=
λ
x
⃗
(
A
−
λ
I
)
x
⃗
=
0
⃗
A
−
λ
I
=
[
5
/
4
−
λ
3
/
4
3
/
4
5
/
4
−
λ
]
d
e
t
(
A
−
λ
I
)
=
0
d
e
t
(
A
−
λ
I
)
=
(
5
4
−
λ
)
2
−
(
3
4
)
2
=
0
λ
1
=
1
2
、
λ
2
=
2
A
x
⃗
1
=
1
2
x
⃗
1
、
A
x
⃗
2
=
2
x
⃗
2
[
5
/
4
3
/
4
3
/
4
5
/
4
]
[
a
1
a
2
]
=
1
2
[
a
1
a
2
]
、
[
5
/
4
3
/
4
3
/
4
5
/
4
]
[
a
3
a
4
]
=
2
[
a
3
a
4
]
a
1
=
−
a
2
、
a
3
=
a
4
W
e
t
a
k
e
a
1
=
−
1
、
a
2
=
1
、
a
3
=
1
、
a
4
=
1
x
⃗
1
=
[
1
1
]
、
x
⃗
2
=
[
−
1
1
]
A=begin{bmatrix}5/4 & 3/4\ 3/4 & 5/4end{bmatrix}\ ~\ Avec{x}=lambda vec{x}\ ~\ (A-lambda I)vec{x}=vec{0}\ ~\ A-lambda I=begin{bmatrix}5/4-lambda & 3/4\ 3/4 & 5/4-lambdaend{bmatrix}\ ~\ det(A-lambda I)=0\ ~\ det(A-lambda I)=(frac{5}{4}-lambda)^2-(frac{3}{4})^2=0\ ~\ lambda_1=frac{1}{2}、lambda_2=2\ ~\ Avec{x}_1=frac{1}{2}vec{x}_1、Avec{x}_2=2vec{x}_2\ ~\ begin{bmatrix} 5/4 & 3/4\ 3/4 & 5/4 end{bmatrix} begin{bmatrix} a_1\ a_2 end{bmatrix}=frac{1}{2} begin{bmatrix} a_1\ a_2 end{bmatrix}、 begin{bmatrix} 5/4 & 3/4\ 3/4 & 5/4 end{bmatrix} begin{bmatrix} a_3\ a_4 end{bmatrix}=2 begin{bmatrix} a_3\ a_4 end{bmatrix}\ ~\ a_1=-a_2、a_3=a_4\ ~\ We take a_1=-1、a_2=1、a_3=1、a_4=1\ ~\ vec{x}_1= begin{bmatrix} 1\ 1 end{bmatrix}、 vec{x}_2= begin{bmatrix} -1\ 1 end{bmatrix}
A=[5/43/43/45/4] Ax=λx (A−λI)x=0 A−λI=[5/4−λ3/43/45/4−λ] det(A−λI)=0 det(A−λI)=(45−λ)2−(43)2=0 λ1=21、λ2=2 Ax1=21x1、Ax2=2x2 [5/43/43/45/4][a1a2]=21[a1a2]、[5/43/43/45/4][a3a4]=2[a3a4] a1=−a2、a3=a4 We take a1=−1、a2=1、a3=1、a4=1 x1=[11]、x2=[−11]
方法二:
A
=
[
5
/
4
3
/
4
3
/
4
5
/
4
]
d
e
t
A
=
(
5
4
)
2
−
(
3
4
)
2
=
1
=
λ
1
λ
2
t
r
A
=
5
4
+
3
4
=
5
2
=
λ
1
+
λ
2
{
λ
1
λ
2
=
1
λ
1
+
λ
2
=
5
2
λ
1
=
1
2
、
λ
2
=
2
A
x
⃗
1
=
1
2
x
⃗
1
、
A
x
⃗
2
=
2
x
⃗
2
[
5
/
4
3
/
4
3
/
4
5
/
4
]
[
a
1
a
2
]
=
1
2
[
a
1
a
2
]
、
[
5
/
4
3
/
4
3
/
4
5
/
4
]
[
a
3
a
4
]
=
2
[
a
3
a
4
]
a
1
=
−
a
2
、
a
3
=
a
4
W
e
t
a
k
e
a
1
=
−
1
、
a
2
=
1
、
a
3
=
1
、
a
4
=
1
x
⃗
1
=
[
1
1
]
、
x
⃗
2
=
[
−
1
1
]
A=begin{bmatrix}5/4 & 3/4\ 3/4 & 5/4end{bmatrix}\ ~\ det A=(frac{5}{4})^2-(frac{3}{4})^2=1=lambda_1lambda_2\ ~\ tr A=frac{5}{4}+frac{3}{4}=frac{5}{2}=lambda_1+lambda_2\ ~\ begin{cases} lambda_1lambda_2=1\ lambda_1+lambda_2=frac{5}{2} end{cases}\ ~\ lambda_1=frac{1}{2}、lambda_2=2\ ~\ Avec{x}_1=frac{1}{2}vec{x}_1、Avec{x}_2=2vec{x}_2\ ~\ begin{bmatrix} 5/4 & 3/4\ 3/4 & 5/4 end{bmatrix} begin{bmatrix} a_1\ a_2 end{bmatrix}=frac{1}{2} begin{bmatrix} a_1\ a_2 end{bmatrix}、 begin{bmatrix} 5/4 & 3/4\ 3/4 & 5/4 end{bmatrix} begin{bmatrix} a_3\ a_4 end{bmatrix}=2 begin{bmatrix} a_3\ a_4 end{bmatrix}\ ~\ a_1=-a_2、a_3=a_4\ ~\ We take a_1=-1、a_2=1、a_3=1、a_4=1\ ~\ vec{x}_1= begin{bmatrix} 1\ 1 end{bmatrix}、 vec{x}_2= begin{bmatrix} -1\ 1 end{bmatrix}
A=[5/43/43/45/4] det A=(45)2−(43)2=1=λ1λ2 tr A=45+43=25=λ1+λ2 {λ1λ2=1λ1+λ2=25 λ1=21、λ2=2 Ax1=21x1、Ax2=2x2 [5/43/43/45/4][a1a2]=21[a1a2]、[5/43/43/45/4][a3a4]=2[a3a4] a1=−a2、a3=a4 We take a1=−1、a2=1、a3=1、a4=1 x1=[11]、x2=[−11]
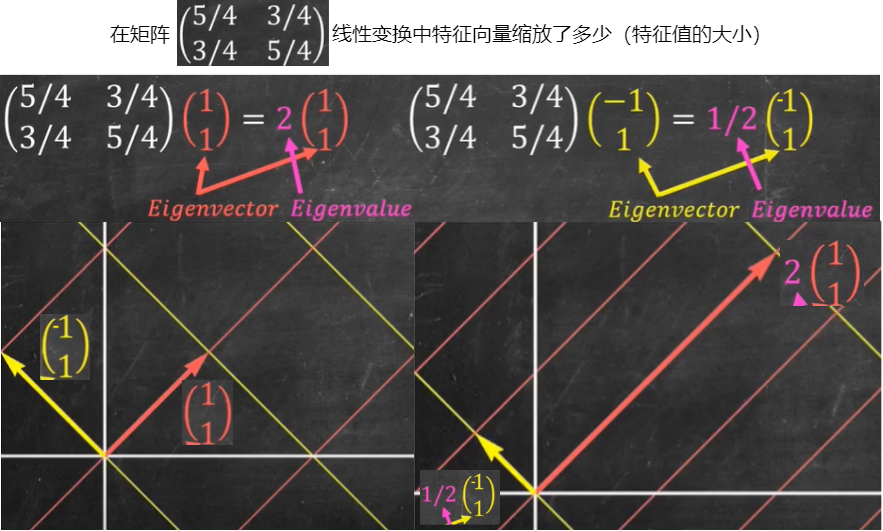
1.3 矩阵对角化
特征向量矩阵
X
X
X
X
=
[
x
⃗
1
x
⃗
2
]
=
[
1
−
1
1
1
]
X=[vec{x}_1quadvec{x}_2]= begin{bmatrix} 1 & -1\ 1 & 1 end{bmatrix}
X=[x1x2]=[11−11]
特征值矩阵
Λ
Lambda
Λ
Λ
=
[
λ
1
0
0
λ
2
]
=
[
2
0
0
1
/
2
]
Lambda= begin{bmatrix} lambda_1 & 0\ 0 & lambda_2 end{bmatrix}= begin{bmatrix} 2 & 0\ 0 & 1/2 end{bmatrix}
Λ=[λ100λ2]=[2001/2]
特征向量矩阵的逆矩阵
X
−
1
X^{-1}
X−1
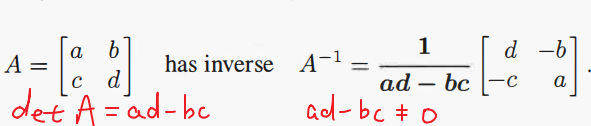
X − 1 = 1 d e t X [ 1 1 − 1 1 ] = 1 2 [ 1 1 − 1 1 ] = [ 1 / 2 1 / 2 − 1 / 2 1 / 2 ] X^{-1}=frac{1}{det X} begin{bmatrix} 1 & 1\ -1 & 1 end{bmatrix}=frac{1}{2} begin{bmatrix} 1 & 1\ -1 & 1 end{bmatrix}= begin{bmatrix} 1/2 & 1/2\ -1/2 & 1/2 end{bmatrix} X−1=det X1[1−111]=21[1−111]=[1/2−1/21/21/2]
将矩阵
A
A
A 进行分解
A
=
X
Λ
X
−
1
=
[
1
−
1
1
1
]
[
2
0
0
1
/
2
]
[
1
/
2
1
/
2
−
1
/
2
1
/
2
]
A=XLambda X^{-1}= begin{bmatrix} 1 & -1\ 1 & 1 end{bmatrix} begin{bmatrix} 2 & 0\ 0 & 1/2 end{bmatrix} begin{bmatrix} 1/2 & 1/2\ -1/2 & 1/2 end{bmatrix}
A=XΛX−1=[11−11][2001/2][1/2−1/21/21/2]
其中 X X X 是由矩阵的各个特征向量组成的矩阵、 Λ Lambda Λ 是由矩阵的各个特征值组成的

对矩阵
X
、
Λ
、
X
−
1
X、Lambda、X^{-1}
X、Λ、X−1 对应的线性变换过程的可视化
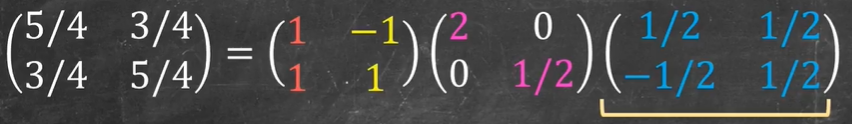
矩阵
X
−
1
X^{-1}
X−1 将特征向量转换到了标准基的位置(我们将此时的特征向量称其为特征基)

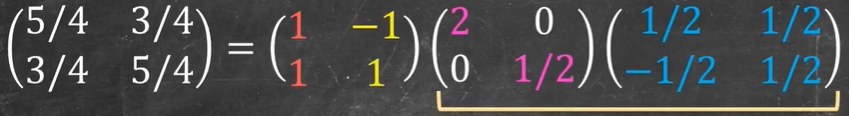
矩阵
Λ
Lambda
Λ 将特征基缩放了特征值大小
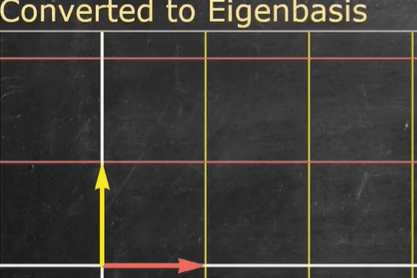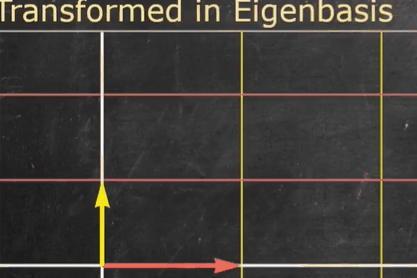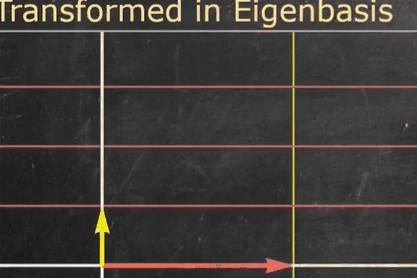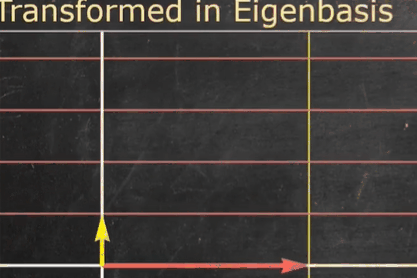
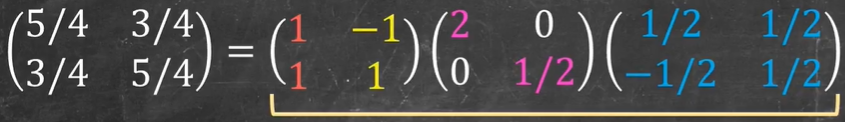
矩阵
X
X
X 将缩放后的特征基转换到特征向量的原本位置(原标准基的坐标系下)

1.4 计算 A k A^k Ak
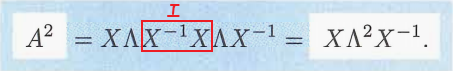
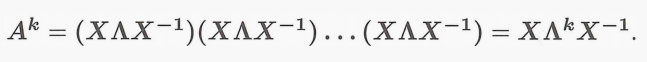
例子:
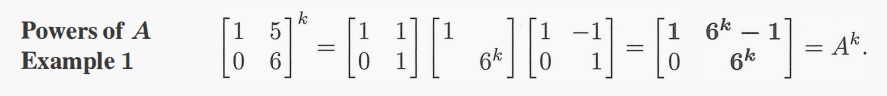

1.5 矩阵对角化的注意事项

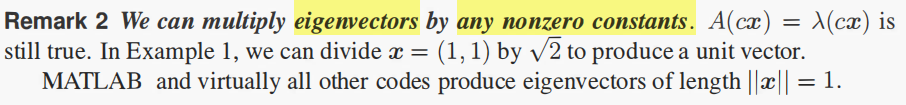
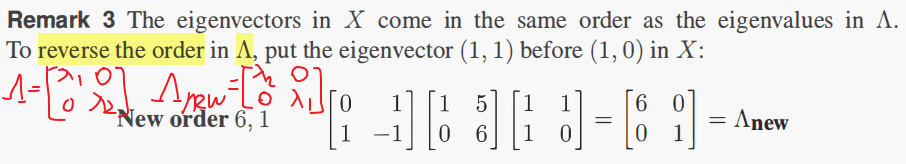

可逆性与可对角化性无关!!!

最后
以上就是谨慎百合最近收集整理的关于矩阵对角化(Diagonalizing a Matrix)1.矩阵对角化(Diagonalizing a Matrix)的全部内容,更多相关矩阵对角化(Diagonalizing内容请搜索靠谱客的其他文章。








发表评论 取消回复